Function Repository Resource:

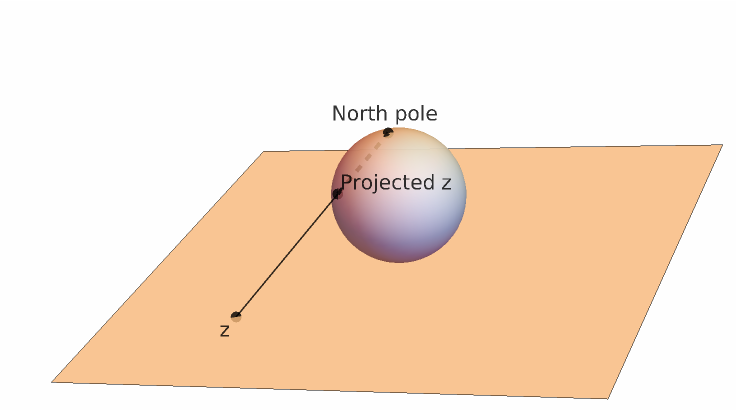
InverseStereographicProjection

Compute the parametrization of a curve projected onto the unit sphere

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["InverseStereographicProjection"][{u,v}]

projects {u,v} from a plane onto the unit sphere.

Details and Options

The projection obtained is generated by projecting points lying in a plane tangent to the south pole of a sphere to the sphere's north pole and plotting the intersection of the projection segment with the sphere.

Examples

Basic Examples (1)

Compute the inverse stereographic projection of a generic point:

In[1]:=

Out[1]=

Scope (3)

Define an ellipse:

In[2]:=

$ellipse[a_, b_][t_] := {a Cos[t], b Sin[t]}$

Project an ellipse onto the sphere:

In[3]:=

Out[3]=

Plot the projected ellipse:

In[4]:=

$Manipulate[ Show[Graphics3D[{Opacity[.5], Sphere[]}], ParametricPlot3D[ ResourceFunction["InverseStereographicProjection"][ ellipse[a, b][t]], {t, 0, 2 \[Pi]}]], {{a, 1.5}, .1, 5}, {{b, 3}, .1, 5}]$

Out[4]=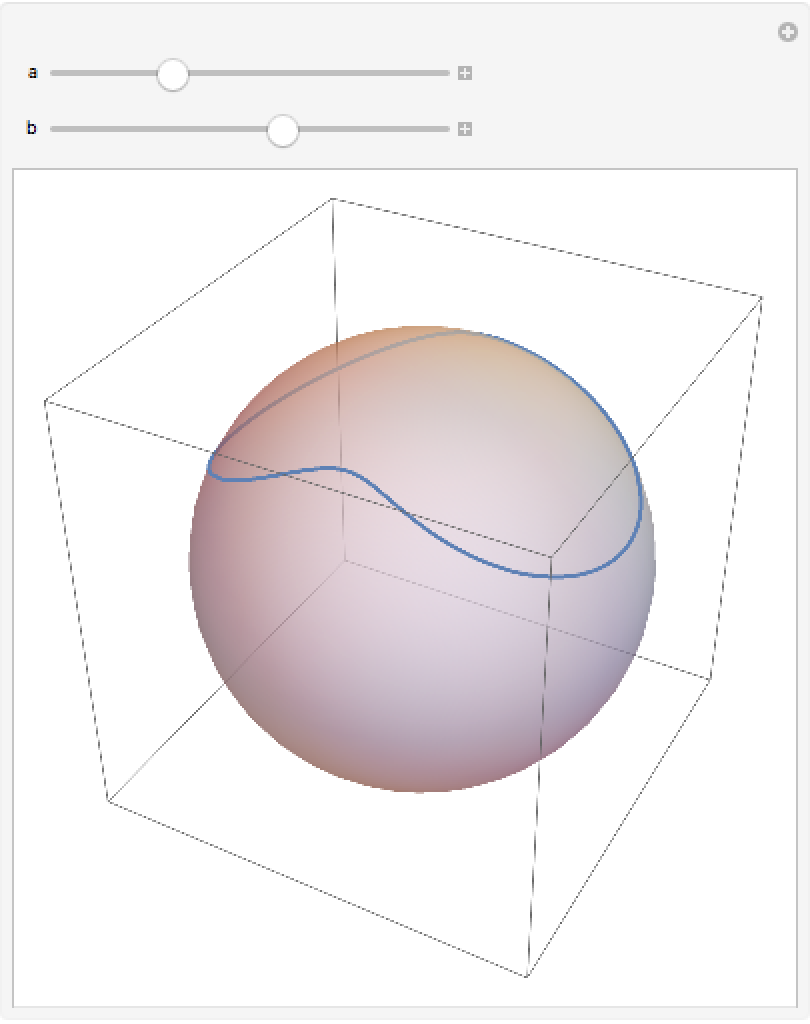

Define a logarithmic spiral curve:

In[5]:=

Out[5]=

A plot of the logarithmic spiral:

In[6]:=

$ParametricPlot[ Evaluate[logspiral /. {a -> 1, b -> .1}], {t, 0, 10 \[Pi]}]$

Out[6]=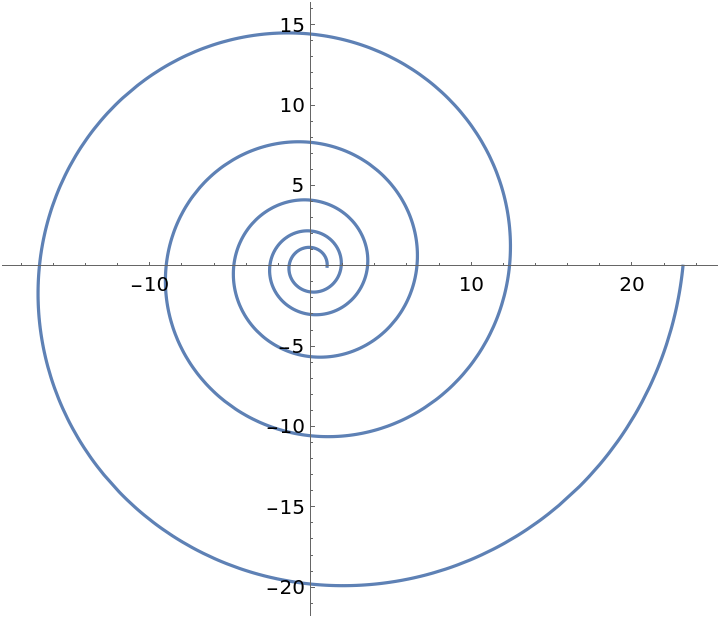

Project the spiral onto the sphere; it becomes a spherical loxodrome:

In[7]:=

Out[7]=

Compute the norm of the logarithmic spiral:

In[8]:=

Out[8]=

Plot the projected spiral with meridians:

In[9]:=

$Show[ParametricPlot3D[ Evaluate[Table[ Entity["Surface", "Sphere"]["ParametricEquations"][1][u, v], {u, 0, 2 \[Pi], \[Pi]/12}]], {v, -\[Pi], \[Pi]}, PlotStyle -> Opacity[.5], Boxed -> False, Axes -> False], ParametricPlot3D[ Evaluate[sphericalloxodrome /. {a -> 1, b -> .15}], {t, -20, 20 \[Pi]}]]$

Out[9]=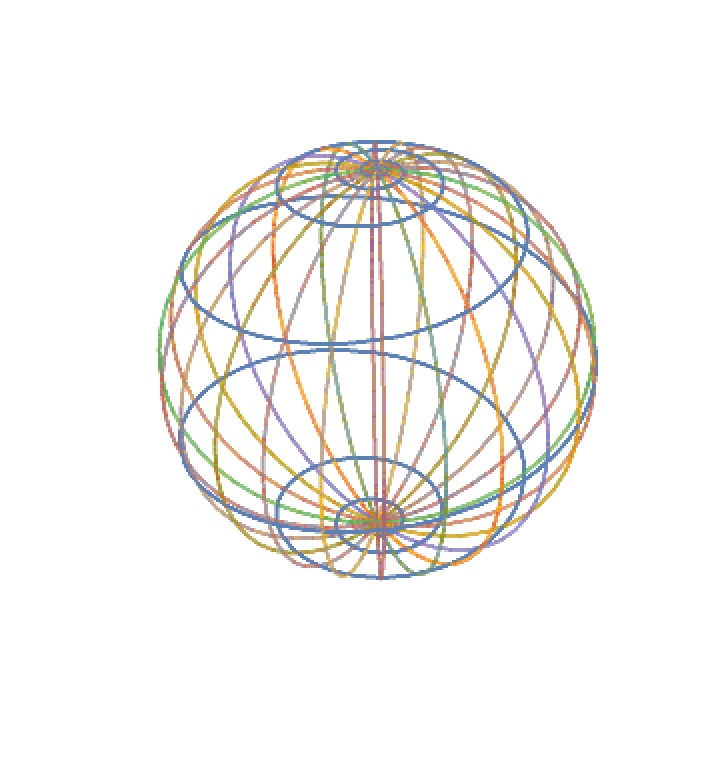

Plot the spherical loxodrome:

In[10]:=

$Manipulate[ Show[Graphics3D[{Opacity[.5], Sphere[]}], ParametricPlot3D[{(2 a E^(b t) Cos[t])/(1 + a^2 E^(2 b t)), ( 2 a E^(b t) Sin[t])/(1 + a^2 E^(2 b t)), (-1 + a^2 E^(2 b t))/( 1 + a^2 E^(2 b t))}, {t, 0, 20 \[Pi]}]], {a, .1, 2}, {b, .1, 2}]$

Out[10]=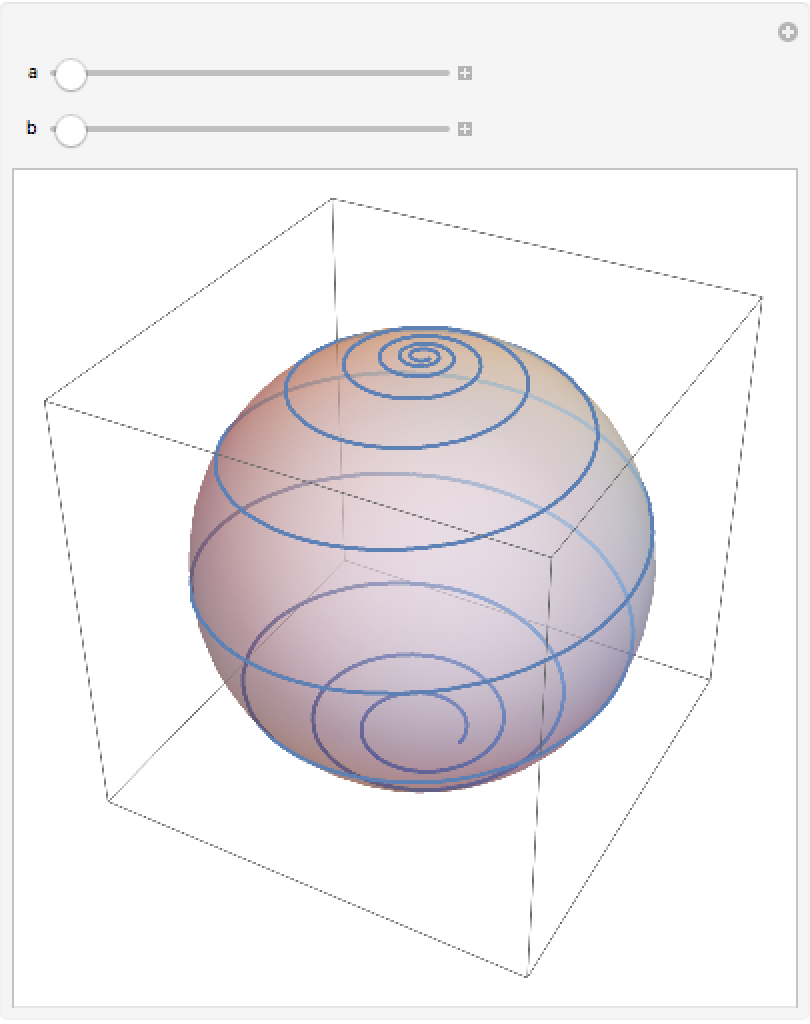

Define the second butterfly curve:

In[11]:=

Out[11]=

Project the curve onto the sphere:

In[12]:=

proj = ResourceFunction["InverseStereographicProjection"][
Entity["PlaneCurve", "ButterflyCurve2"]["ParametricEquations"][3][
t]] // Simplify

Out[12]=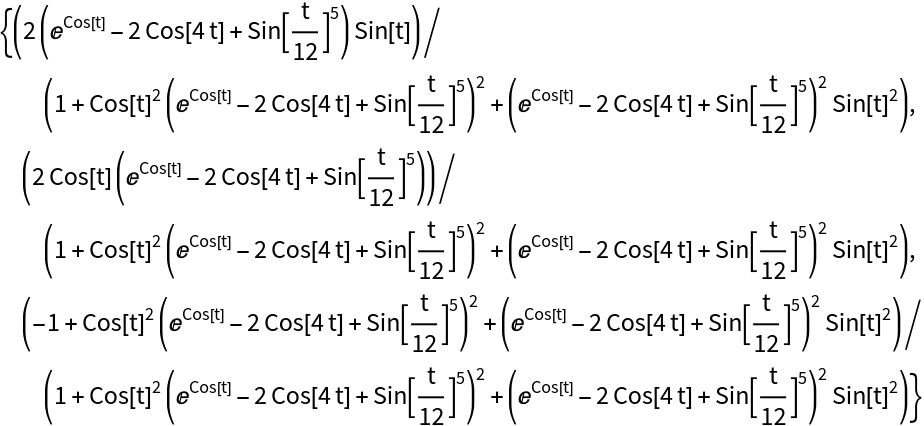

Plot the curve and the projection:

In[13]:=

$Show[Graphics3D[{Opacity[.5], Sphere[]}, Boxed -> False], ParametricPlot3D[proj, {t, 0, 20 \[Pi]}, PlotStyle -> Green], ParametricPlot3D[Evaluate[Append[sbc, -1]], {t, 0, 20 \[Pi]}, PlotPoints -> 500]]$

Out[13]=

Properties and Relations (3)

The norm of the stereographic sphere:

In[14]:=

Out[14]=

Project a grid of points in Cartesian coordinates:

In[15]:=

A Cartesian grid on the plane appears distorted on the sphere; show the points and their projections onto the sphere:

In[16]:=

Show[Graphics3D[{Point[Append[#, -1] & /@ points], Green, Point[ResourceFunction["InverseStereographicProjection"] /@ points], Opacity[.5], Red, Sphere[]}, Boxed -> False]]

Out[16]=

Project a grid of lines instead:

In[17]:=

Show the lines and their projections:

In[18]:=

Show[Graphics3D[{Opacity[.5], Sphere[]}, Boxed -> False], ParametricPlot3D[Evaluate[grid], {t, -2, 2}], ParametricPlot3D[
Evaluate[Append[#, -1] & /@ Join[Table[{t, n}, {n, -2, 2, .5}], Table[{n, t}, {n, -2, 2, .5}]]], {t, -2, 2}, PlotRange -> 2]]

Out[18]=

The same mesh can be generated by ParametricPlot3D. The grid lines are still perpendicular, but the sectors get smaller close to the north pole:

In[19]:=

$ParametricPlot3D[ Evaluate[ResourceFunction[ "InverseStereographicProjection"][{u, v}]], {u, -2 \[Pi], 2 \[Pi]}, {v, -2 \[Pi], 2 \[Pi]}, PlotStyle -> Opacity[.5], PlotRange -> All, PlotPoints -> 80, Boxed -> False, Axes -> False]$