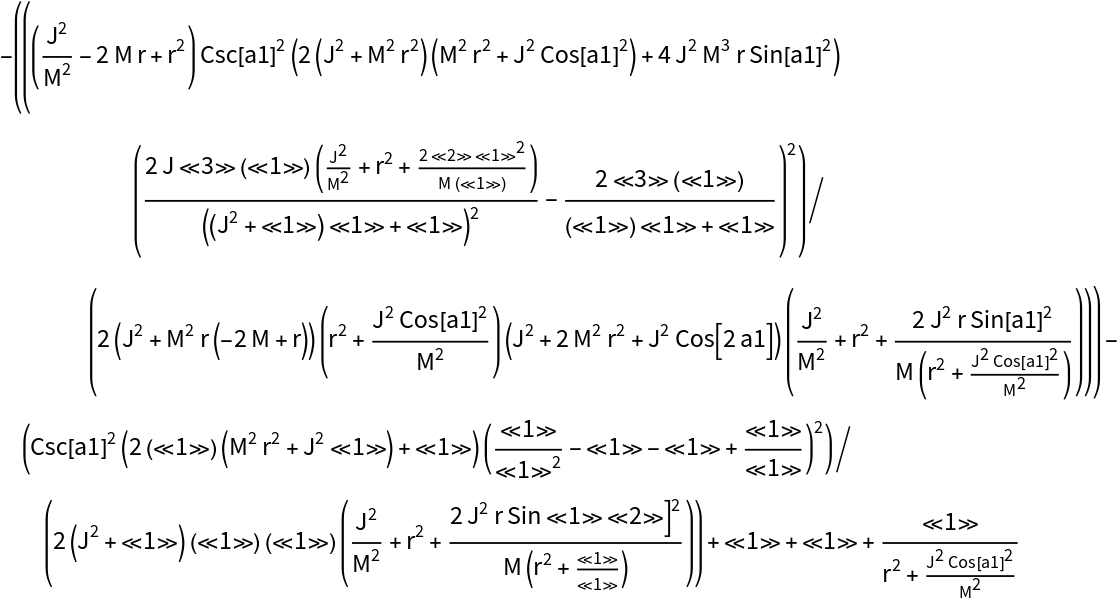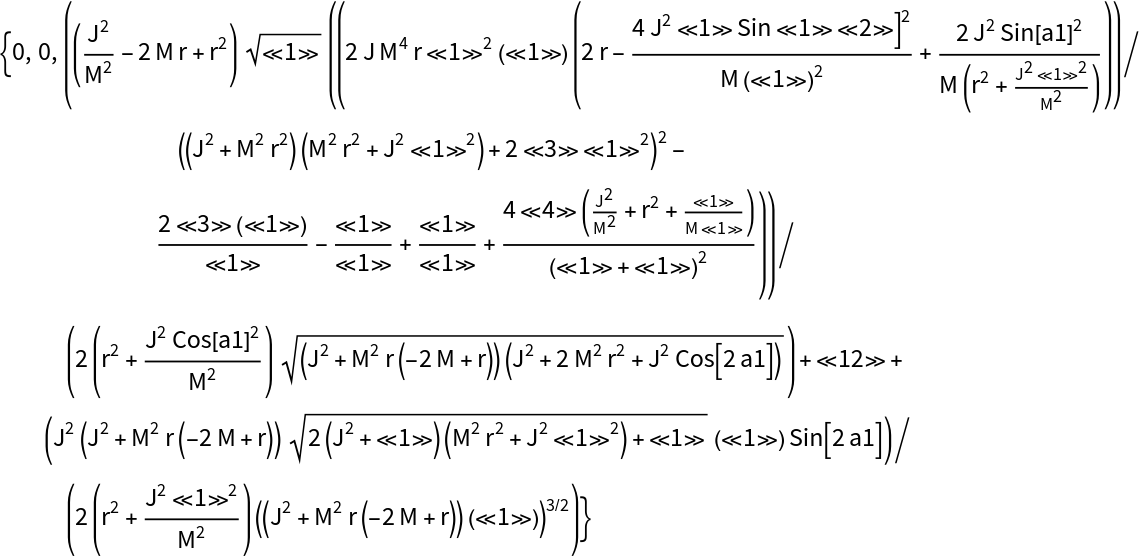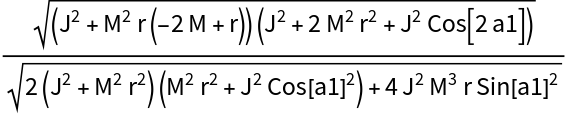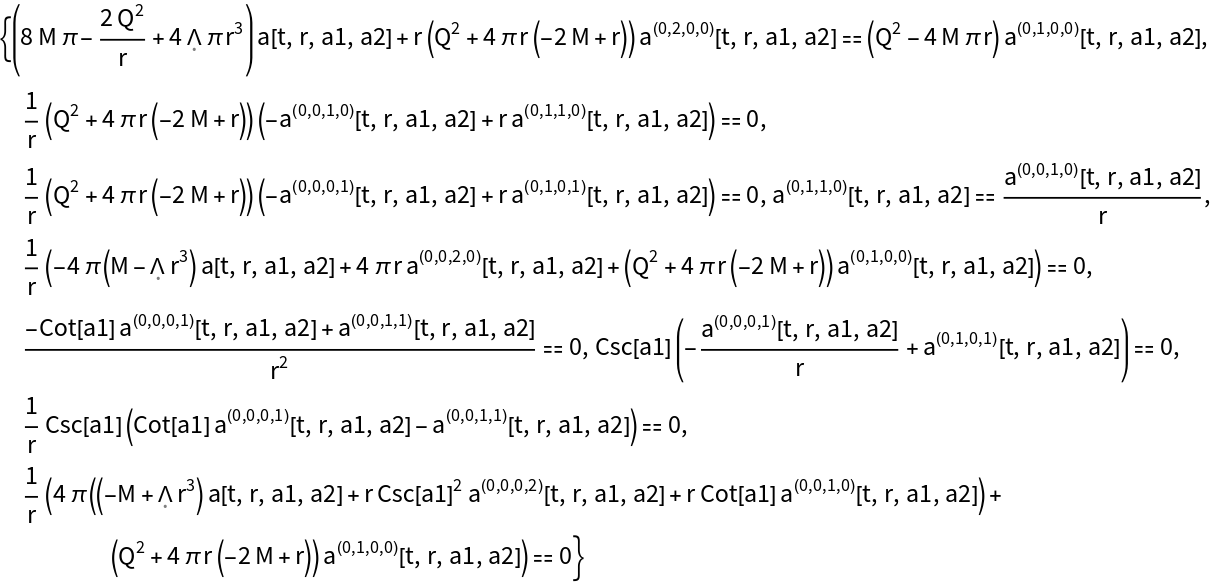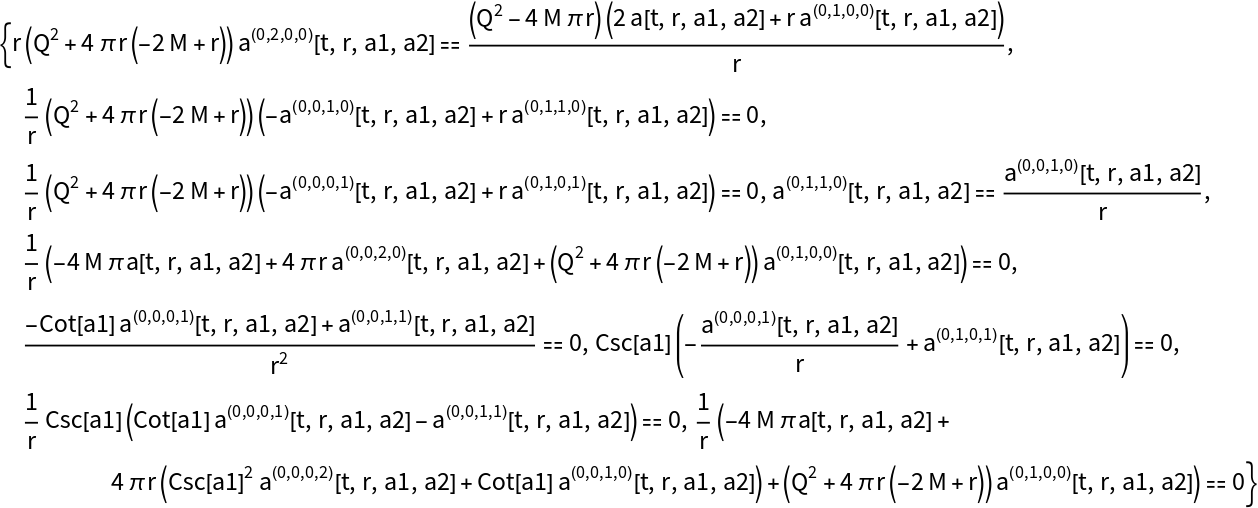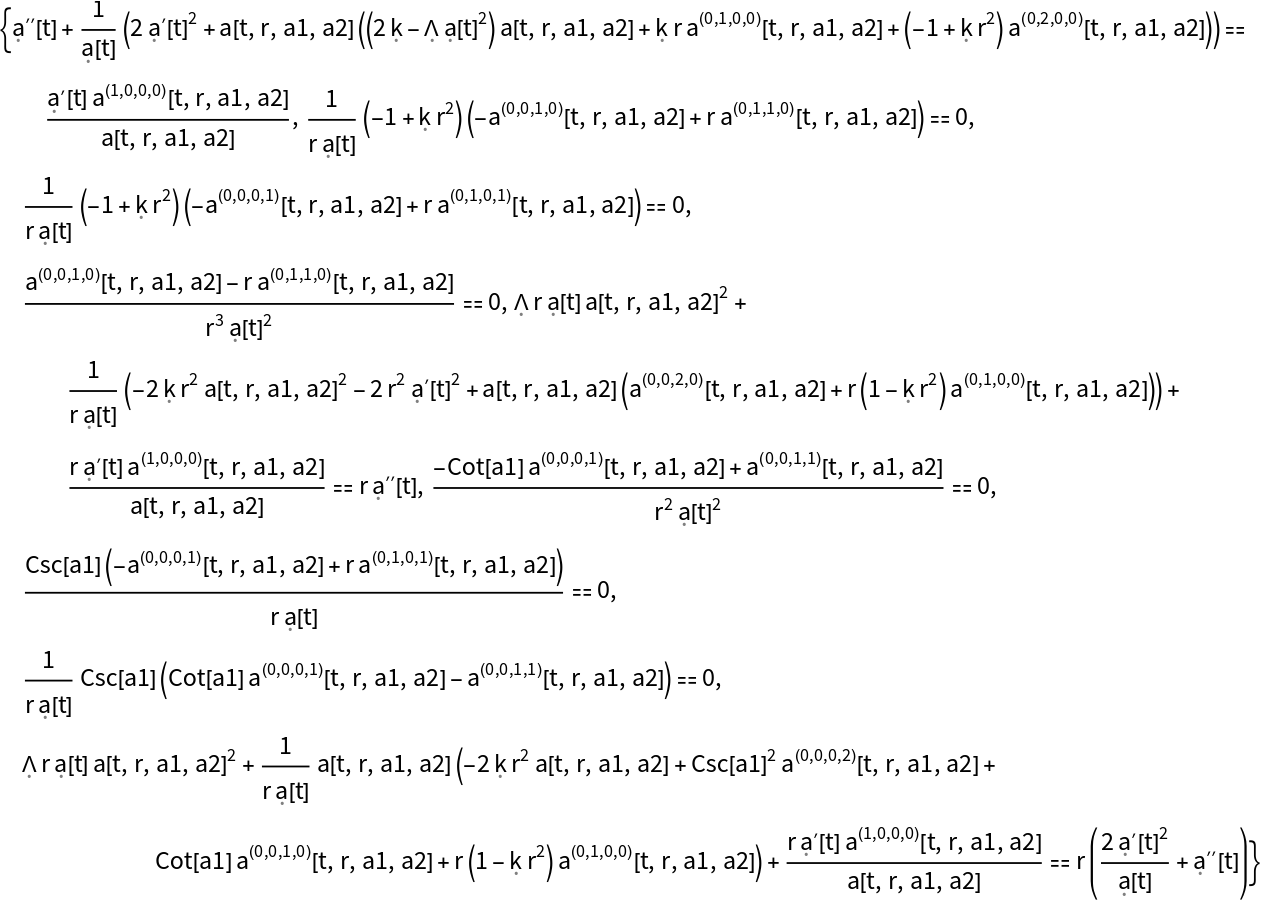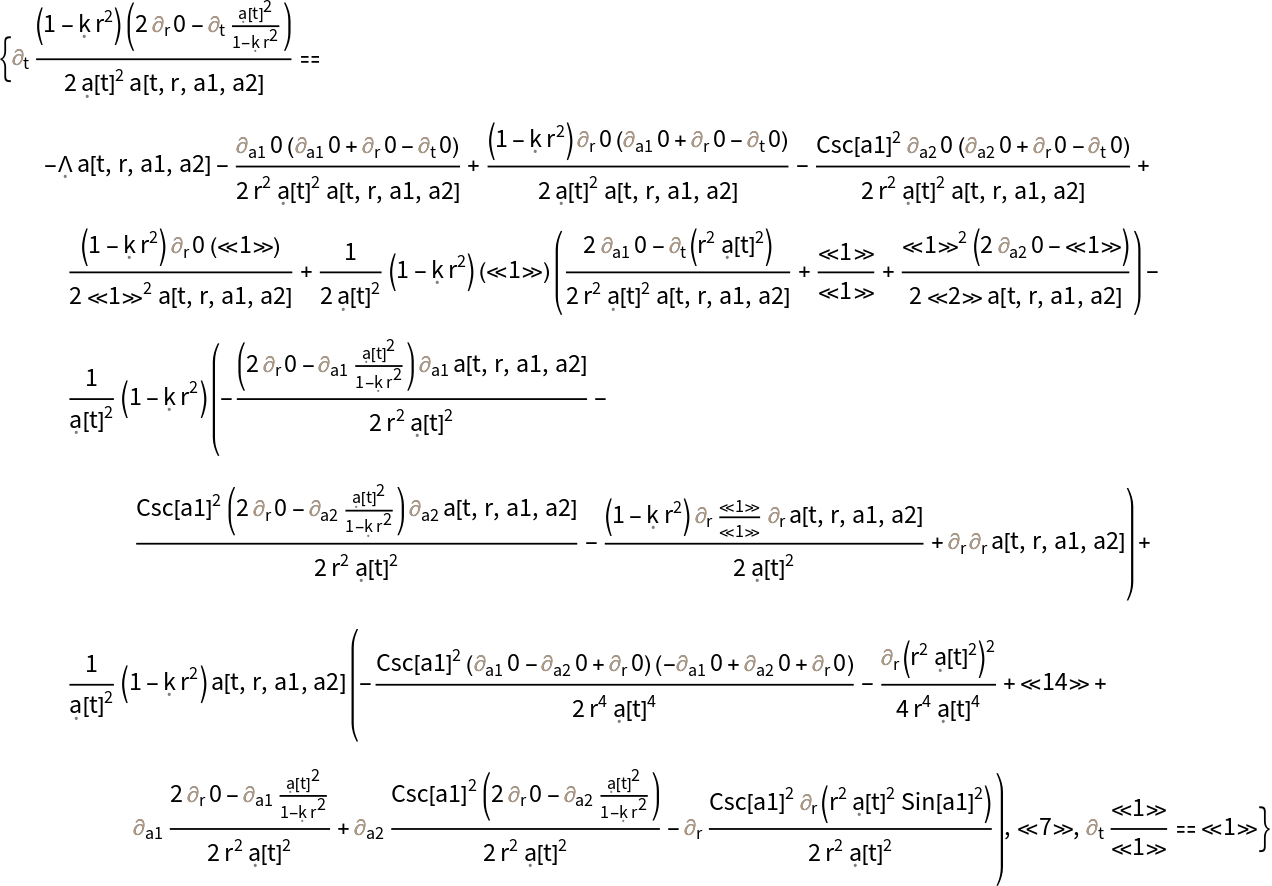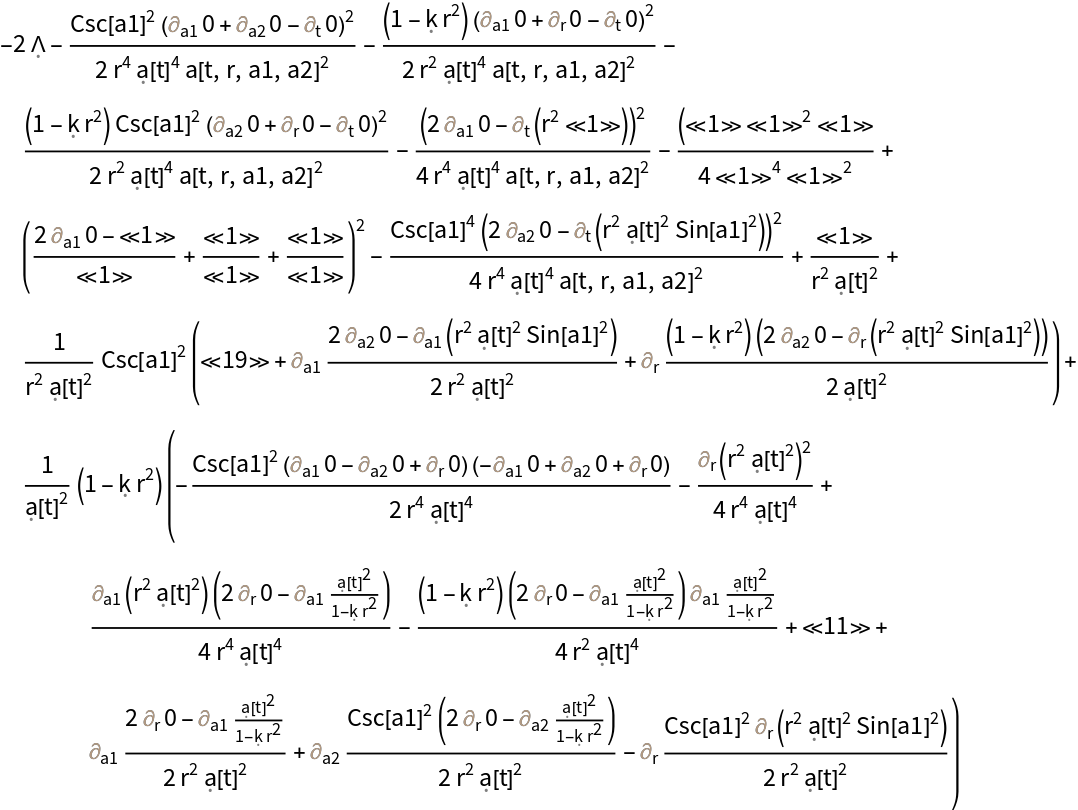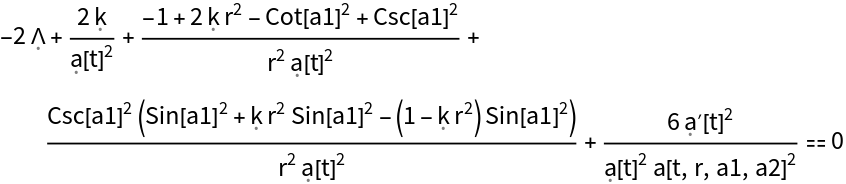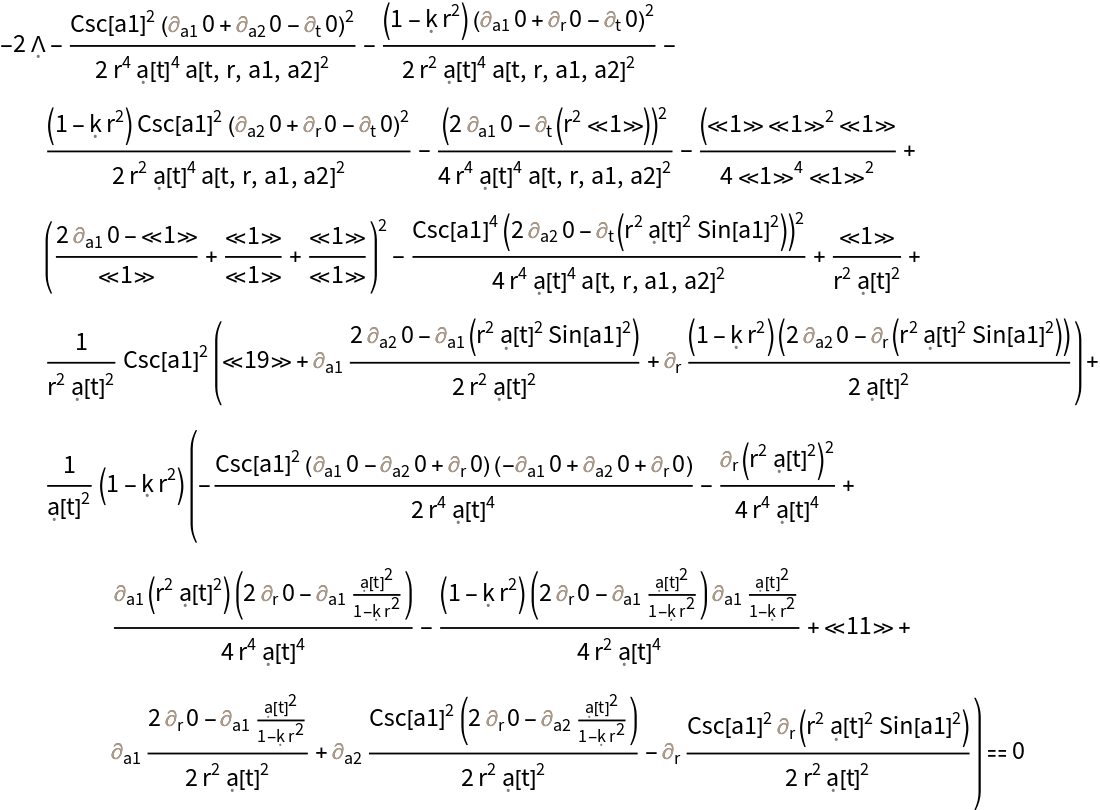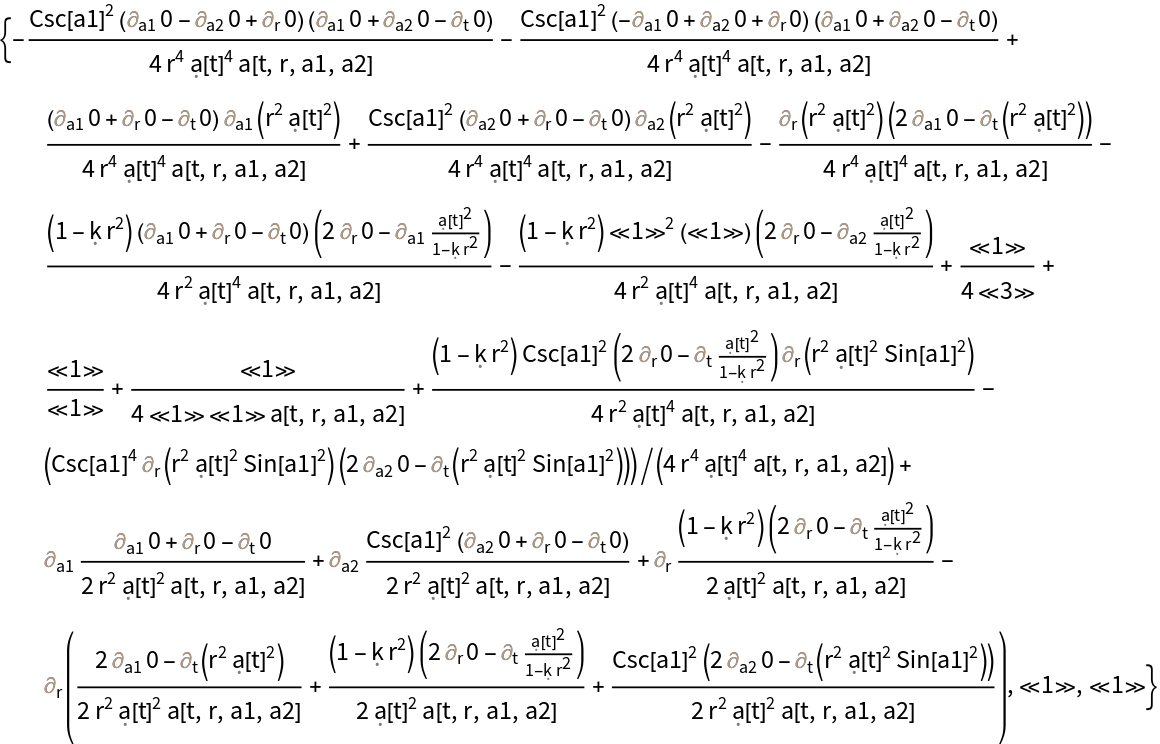Basic Examples (3)
Show that the ADM decomposition for the Schwarzschild metric (e.g. for an uncharged, non-rotating black hole with symbolic mass M) in standard spherical polar coordinates with time coordinate symbol t and spatial coordinate symbols r, a1 and a2, using a partially-constrained choice of gauge (defined in terms of scalar functions a and b), is a valid solution to the vacuum ADM evolution equations with zero cosmological constant:
Show that the (partially-constrained) vacuum ADM Schwarzschild solution is not exact (i.e. additional field equations need to be assumed):
Show the list of vacuum equations of motion describing the evolution of the extrinsic curvature tensor with respect to coordinate time t for the (partially-constrained) vacuum ADM Schwarzschild solution:
Show the list of vacuum equations of motion describing the evolution of the extrinsic curvature tensor with respect to coordinate time t for the (partially-constrained) vacuum ADM Schwarzschild solution, with all algebraic equivalences imposed:
Show that the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (partially-constrained) vacuum ADM Schwarzschild solution does not vanish identically:
Compute the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (partially-constrained) vacuum ADM Schwarzschild solution:
Compute the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (partially-constrained) vacuum ADM Schwarzschild solution, with all algebraic equivalences imposed:
Show that the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (partially-constrained) vacuum ADM Schwarzschild solution do not vanish identically:
Compute the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (partially-constrained) vacuum ADM Schwarzschild solution:
Compute the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (partially-constrained) vacuum ADM Schwarzschild solution, with all algebraic equivalences imposed:
Show that the ADM decomposition for the Schwarzschild metric using a fully-constrained choice of gauge is now an exact solution to the vacuum ADM equations with zero cosmological constant (i.e. no additional field equations need to be assumed):
Show that the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (maximally-constrained) vacuum ADM Schwarzschild solution vanishes identically:
Show that the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (maximally-constrained) vacuum ADM Schwarzschild solution vanish identically:
Show that the ADM decomposition for the Schwarzschild metric using a geodesic slicing condition on the lapse (i.e. the lapse function is identically one) and normal coordinate conditions on the shift (i.e. the shift vector is identically zero) is only a valid solution to the vacuum ADM equations with zero cosmological constant if either the mass of the black hole is equal to zero or the value of the radial coordinate is equal to infinity:
Find the conditions under which the ADM decomposition for the Friedmann-Lemaître-Robertson-Walker (FLRW) metric (for a homogeneous, isotropic and uniformly-expanding/contracting universe, with symbolic curvature parameter "k" and symbolic scale factor "a") in standard spherical polar coordinates with time coordinate symbol t and spatial coordinate symbols r, a1 and a2, using a partially-constrained choice of gauge (defined in terms of scalar function a), is a valid solution to the vacuum ADM evolution equations with symbolic cosmological constant "":
Find the condition under which the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (partially-constrained) ADM FLRW solution vanishes identically:
Find the condition under which the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (partially-constrained) ADM FLRW solution vanishes identically, with all algebraic equivalences imposed:
Find the conditions under which the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (partially-constrained) ADM FLRW solution vanish identically:
Find the conditions under which the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (partially-constrained) ADM FLRW solution vanish identically, with all algebraic equivalences imposed:
Find the corresponding conditions for the case of zero cosmological constant:
Show that in neither case is the solution exact (i.e. additional field equations must be assumed):
Show that the ADM decomposition for the Kerr metric (e.g. for an uncharged, spinning black hole with symbolic mass M and symbolic angular momentum J) in Boyer-Lindquist/oblate spheroidal coordinates with time coordinate symbol t and spatial coordinate symbols r, a1 and a2, using an appropriate maximally-constrained choice of gauge, is a valid (exact) solution to the vacuum ADM evolution equations with zero cosmological constant:
Show the list of vacuum equations of motion describing the evolution of the extrinsic curvature tensor with respect to coordinate time t for the (maximally-constrained) vacuum ADM Kerr solution:
Show the list of vacuum equations of motion describing the evolution of the extrinsic curvature tensor with respect to coordinate time t for the (maximally-constrained) vacuum ADM Kerr solution, with all algebraic equivalences imposed, and confirm that they hold identically:
Show that the Hamiltonian constraint (derived from the timelike component of the contracted Bianchi identities) for the (maximally-constrained) vacuum ADM Kerr solution vanishes identically:
Show that the momentum constraints (derived from the spacelike components of the contracted Bianchi identities) for the (maximally-constrained) vacuum ADM Kerr solution vanish identically:
Show the lapse function for the (maximally-constrained) vacuum ADM Kerr solution, demonstrating the effects of gravitational time dilation:
Show the shift vector for the (maximally-constrained) vacuum ADM Kerr solution, demonstrating the effects of frame dragging:
Scope (2)
By default, SolveVacuumADMEquations will use a symbolic value ("") for the cosmological constant:
This default choice may be overridden using a second argument:
Solve the vacuum ADM evolution equations for the ADM decomposition of the FLRW metric, with symbolic curvature parameter "k", symbolic scale factor "a" and a partially-constrained choice of gauge (defined in terms of scalar function a), and assuming symbolic cosmological constant "":
Show the list of properties:
Determine whether the ADM decomposition is a valid solution to the vacuum ADM evolution equations:
Determine whether the ADM decomposition is a valid exact solution to the vacuum ADM evolution equations (i.e. no additional field equations need to be assumed):
Show the list of (additional) field equations that must be assumed in order for the ADM decomposition to be a valid solution to the vacuum ADM evolution equations:
Show the list of vacuum ADM evolution equations characterizing the time evolution of components of the extrinsic curvature tensor over submanifolds/spacelike hypersurfaces of the ADM decomposition:
Show the list of vacuum ADM evolution equations characterizing the time evolution of components of the extrinsic curvature tensor over submanifolds/spacelike hypersurfaces of the ADM decomposition, with all algebraic equivalences imposed:
Show the list of vacuum ADM evolution equations characterizing the time evolution of components of the extrinsic curvature tensor over submanifolds/spacelike hypersurfaces of the ADM decomposition, with all partial derivative operators left purely symbolic:
Show the underlying ADM decomposition associated to the vacuum ADM solution:
Show the spatial metric tensor (i.e. the metric tensor on submanifolds/spacelike hypersurfaces) for the vacuum ADM solution:
Show the spacetime metric tensor (i.e. the metric tensor on the ambient manifold/spacetime) for the vacuum ADM solution:
Show the future-pointing, timelike unit vector normal to submanifolds/spacelike hypersurfaces of the vacuum ADM solution:
Show the future-pointing, timelike unit vector normal to submanifolds/spacelike hypersurfaces of the vacuum ADM solution, with all algebraic equivalences imposed:
Show the future-pointing, timelike unit vector normal to submanifolds/spacelike hypersurfaces of the vacuum ADM solution, with all partial derivative operators left purely symbolic:
Show the future-pointing, timelike "time vector" for the vacuum ADM solution:
Show the future-pointing, timelike "time vector" for the vacuum ADM solution, with all partial derivative operators left purely symbolic:
Show the distinguished time coordinate symbol for the vacuum ADM solution:
Show the list of distinguished spatial coordinate symbols for the vacuum ADM solution:
Show the list of differential 1-form symbols for the (ambient/spacetime) coordinates of the vacuum ADM solution:
Show the lapse function for the vacuum ADM solution:
Show the shift vector (field) for the vacuum ADM solution:
Determine whether the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution vanishes identically:
Show the value of the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution:
Show the value of the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution, with all algebraic equivalences imposed:
Show the value of the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution, with all partial derivative operators left purely symbolic:
Show the condition required to guarantee that the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution vanishes identically:
Show the condition required to guarantee that the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution vanishes identically, with all algebraic equivalences imposed:
Show the condition required to guarantee that the Hamiltonian constraint (i.e. the timelike component of the contracted Bianchi identities) for the vacuum ADM solution vanishes identically, with all partial derivative operators left purely symbolic:
Determine whether the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution vanish identically:
Show the list of values of the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution:
Show the list of values of the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution, with all algebraic equivalences imposed:
Show the list of values of the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution, with all partial derivative operators left purely symbolic:
Show the list of conditions required to guarantee that the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution vanish identically:
Show the list of conditions required to guarantee that the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution vanish identically, with all algebraic equivalences imposed:
Show the list of conditions required to guarantee that the momentum constraints (i.e. the spacelike components of the contracted Bianchi identities) for the vacuum ADM solution vanish identically, with all partial derivative operators left purely symbolic:
Show the value of the cosmological constant for the vacuum ADM solution:
Show the number of dimensions of the ambient manifold/spacetime represented by the vacuum ADM solution:
Show the signature of the ambient manifold/spacetime represented by the vacuum ADM solution (with +1s representing positive eigenvalues and -1s representing negative eigenvalues of the metric tensor):
Determine whether the ambient manifold/spacetime represented by the vacuum ADM solution is Riemannian (i.e. all eigenvalues of the metric tensor have the same sign):
Determine whether the ambient manifold/spacetime represented by the vacuum ADM solution is pseudo-Riemannian (i.e. all eigenvalues are non-zero, but not all have the same sign):
Determine whether the ambient manifold/spacetime represented by the vacuum ADM solution is Lorentzian (i.e. all eigenvalues of the metric tensor have the same sign, except for one eigenvalue which has the opposite sign):
Show the list of conditions on the coordinates required to guarantee that the ambient manifold/spacetime represented by the vacuum ADM solution is Riemannian (i.e. all eigenvalues of the metric tensor are positive):
Show the list of conditions on the coordinates required to guarantee that the ambient manifold/spacetime represented by the vacuum ADM solution is pseudo-Riemannian (i.e. all eigenvalues of the metric tensor are non-zero):
Show the list of conditions on the coordinates required to guarantee that the ambient manifold/spacetime represented by the vacuum ADM solution is Lorentzian (i.e. the "time" eigenvalue is negative, and all other eigenvalues are positive):
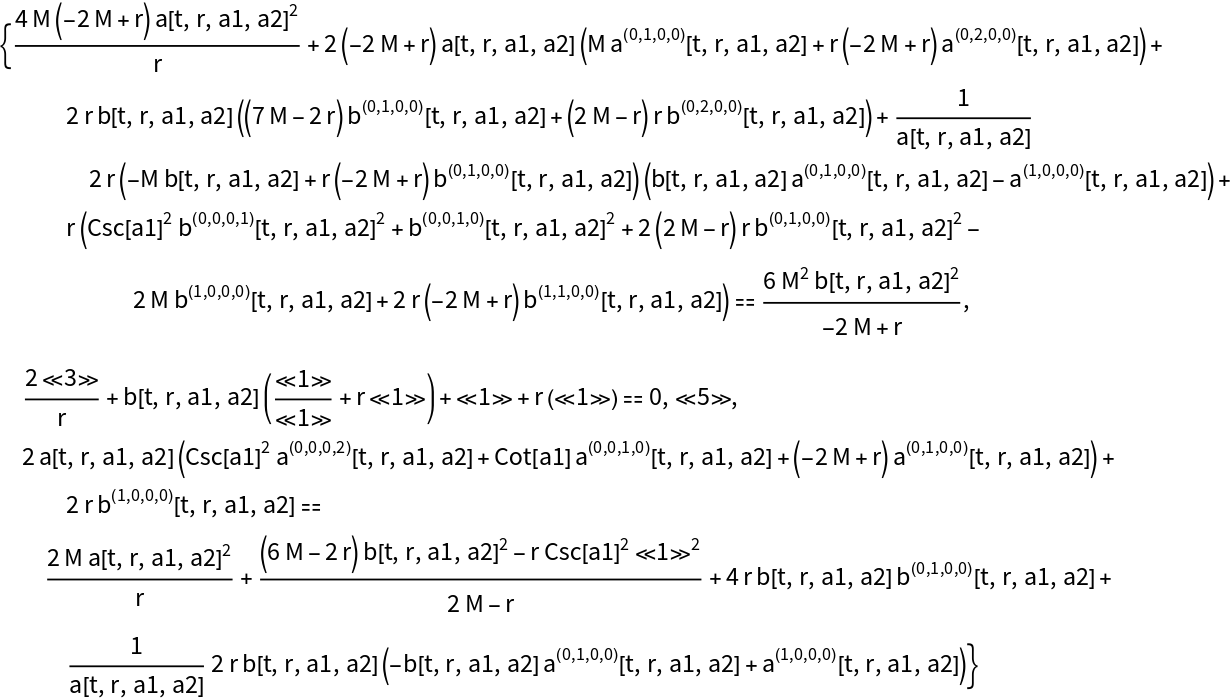

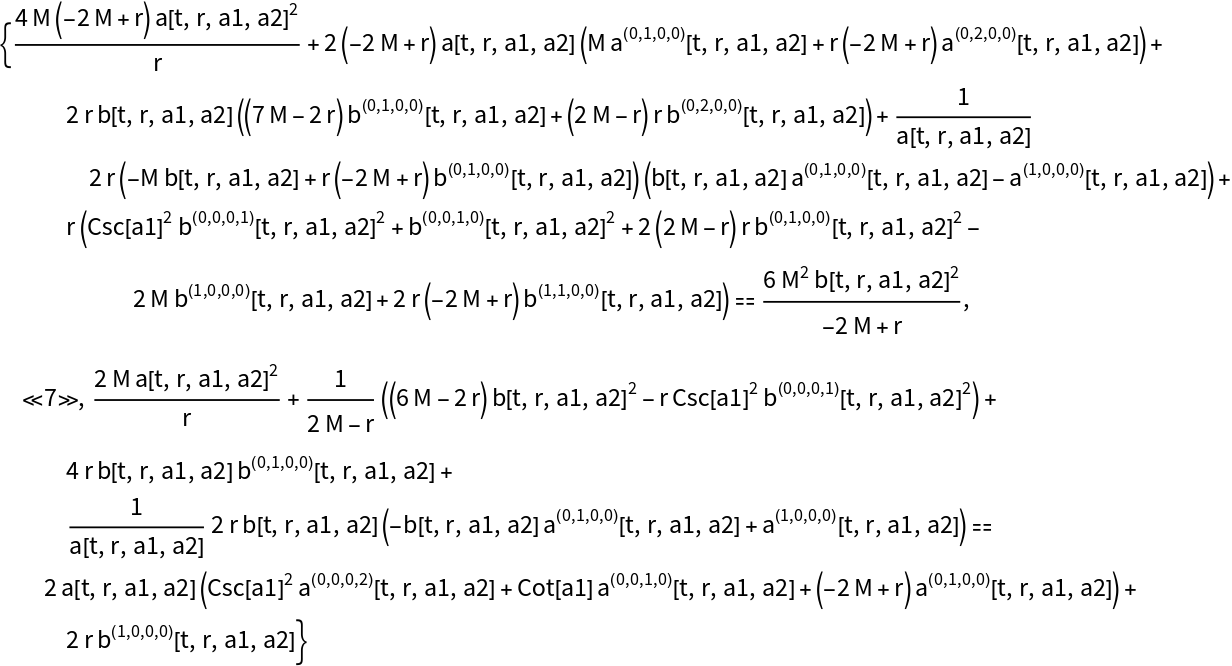
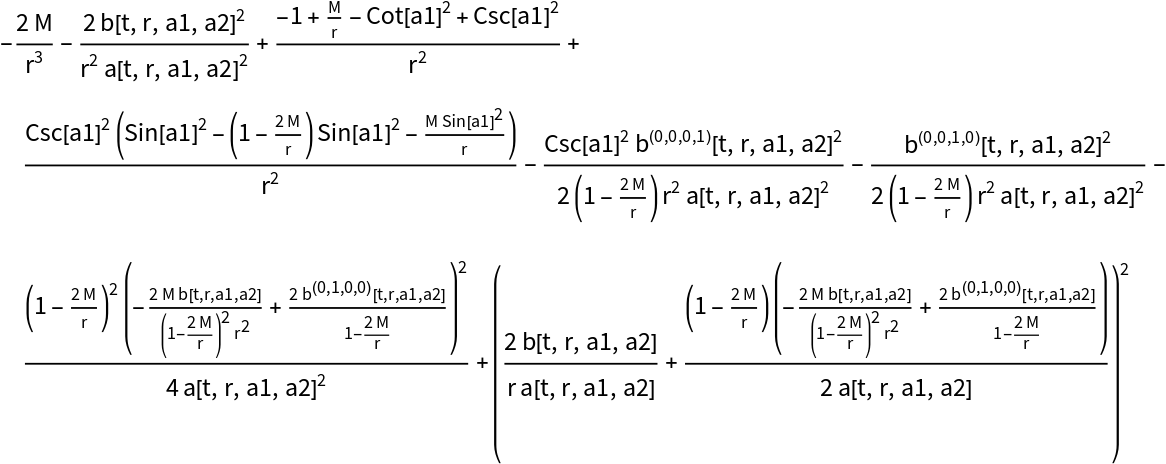
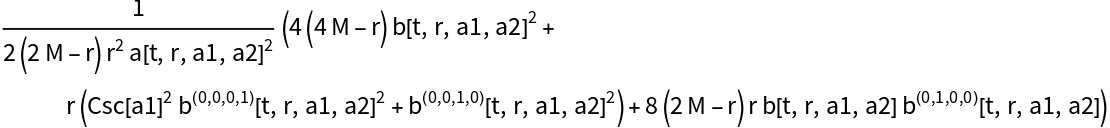


![adm2 = ResourceFunction["ADMDecomposition"][{"Schwarzschild", M}, t, {r, a1, a2}, Sqrt[1 - 2 M/r], {0, 0, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/52e/52efe2e3-2a78-4ac9-997a-7ba87d297b95/7cb135212562101d.png)

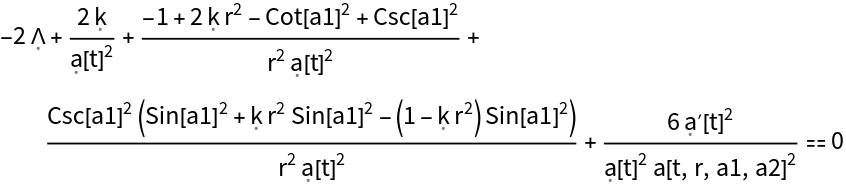

![adm = ResourceFunction["ADMDecomposition"][{"Kerr", M, J}, t, {r, a1, a2}, Sqrt[(J^2 + M^2 r (-2 M + r)) (J^2 + 2 M^2 r^2 + J^2 Cos[2 a1])]/
Sqrt[2 (J^2 + M^2 r^2) (M^2 r^2 + J^2 Cos[a1]^2) + 4 J^2 M^3 r Sin[a1]^2], {0, 0, -((2 J M^4 r)/((J^2 + M^2 r^2) (M^2 r^2 + J^2 Cos[a1]^2) + 2 J^2 M^3 r Sin[a1]^2))}]](https://www.wolframcloud.com/obj/resourcesystem/images/52e/52efe2e3-2a78-4ac9-997a-7ba87d297b95/47acb2cfcdcaf501.png)