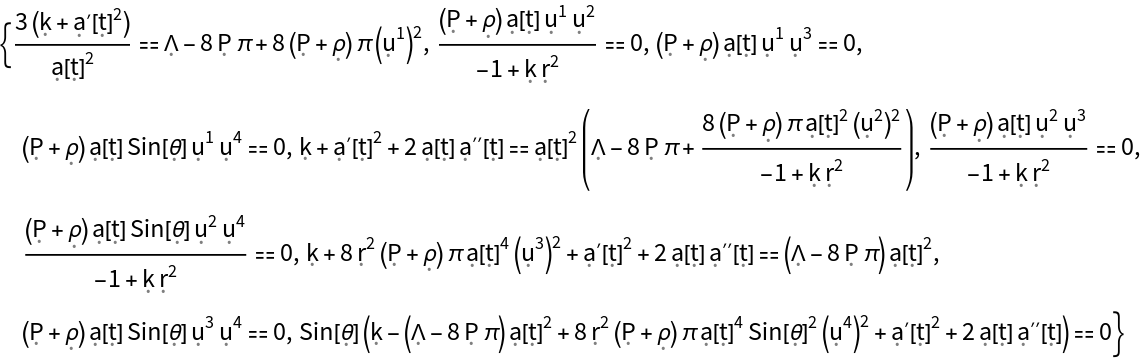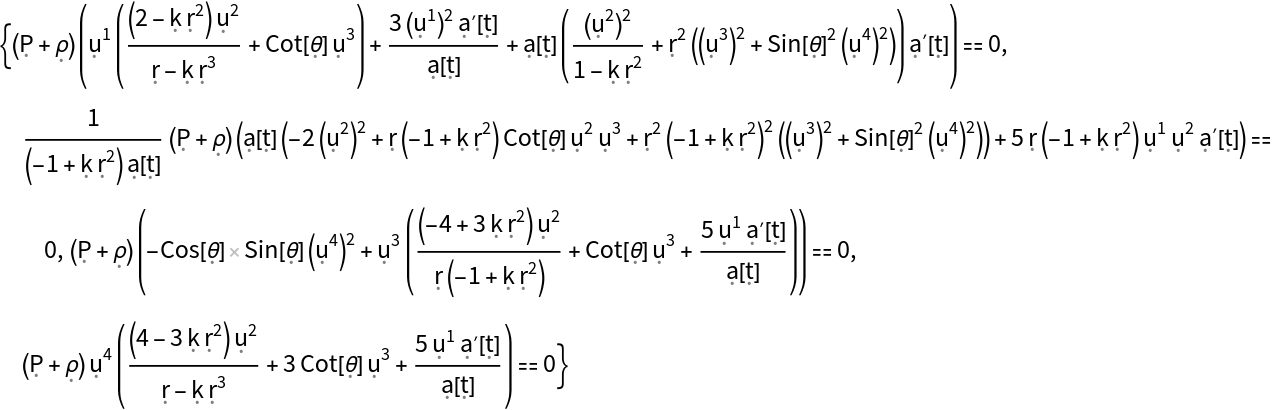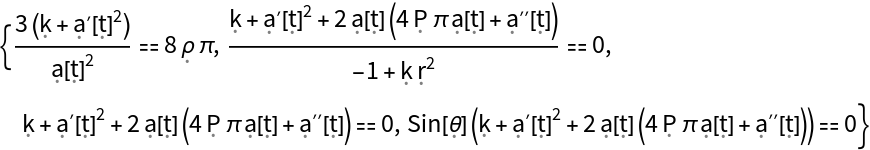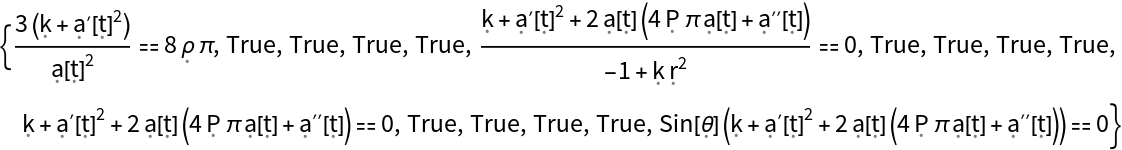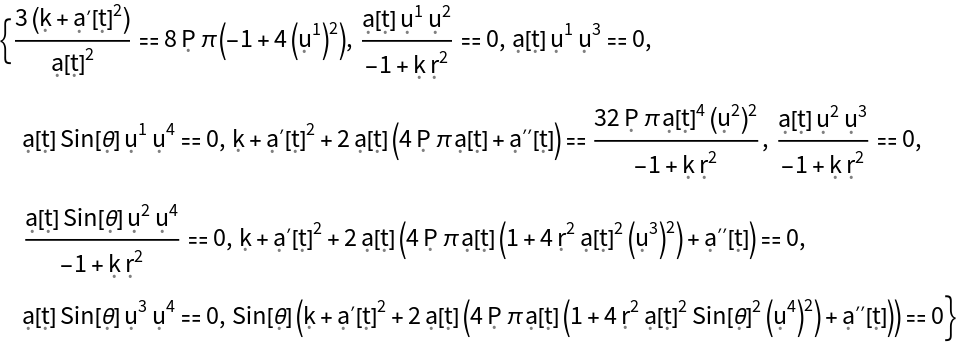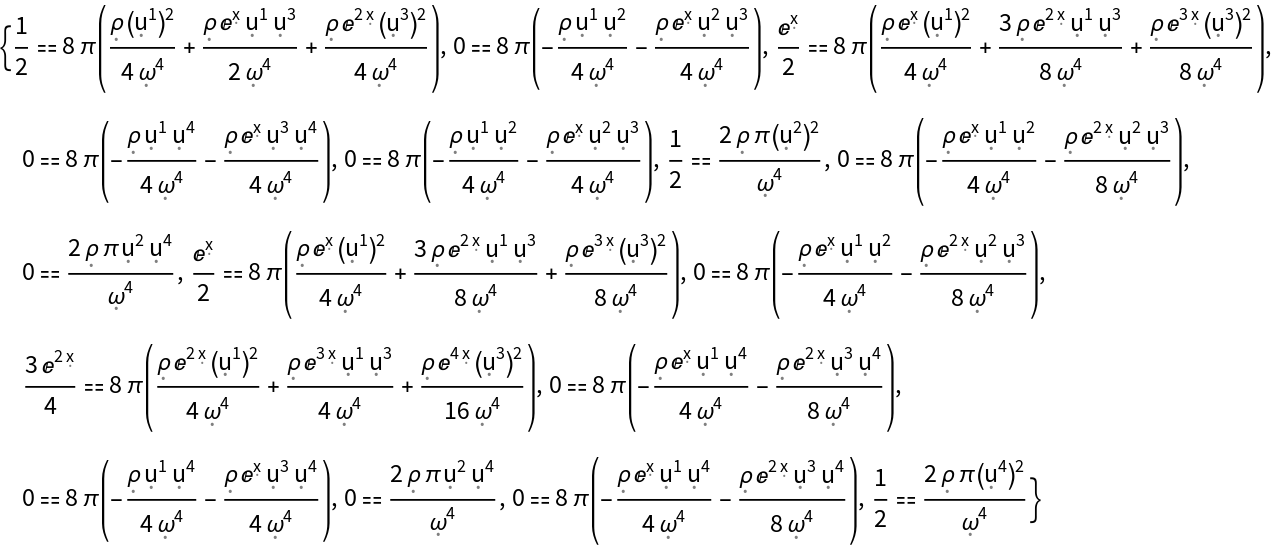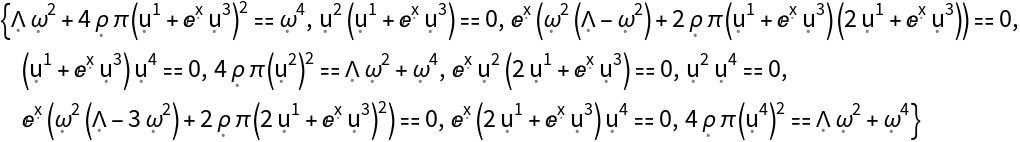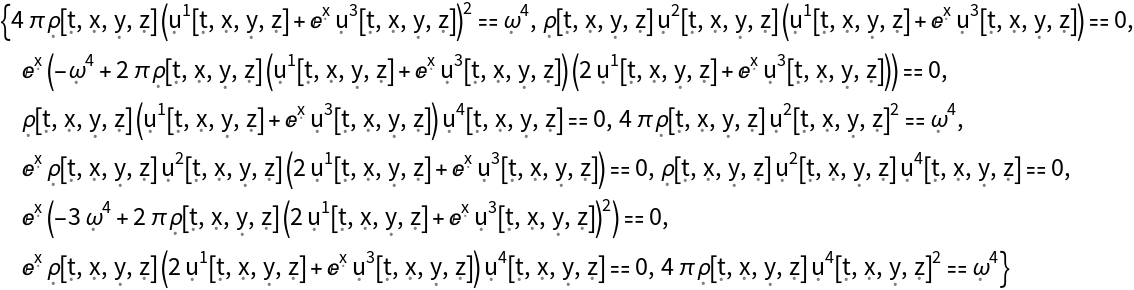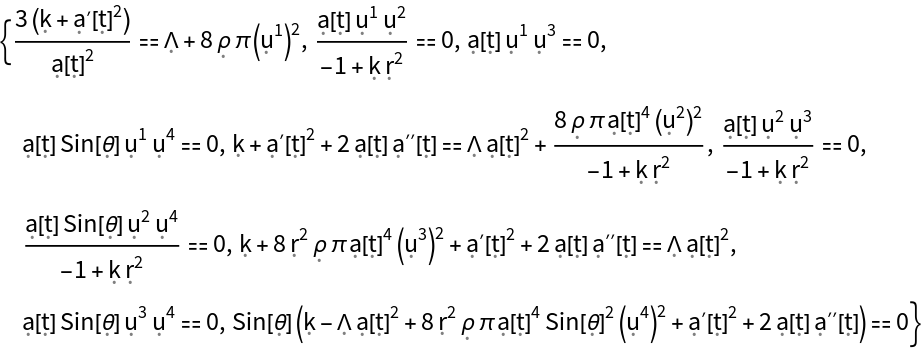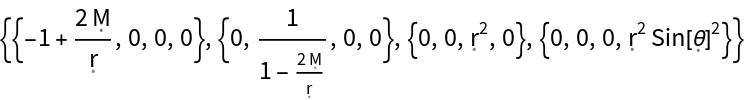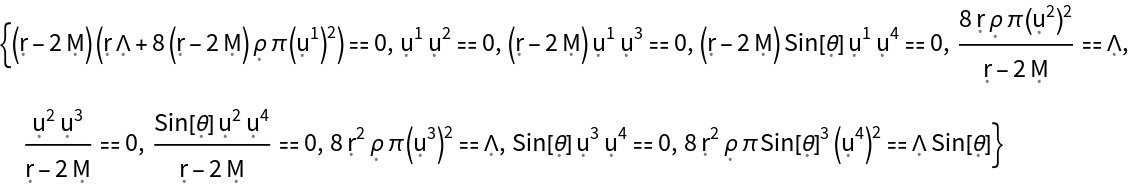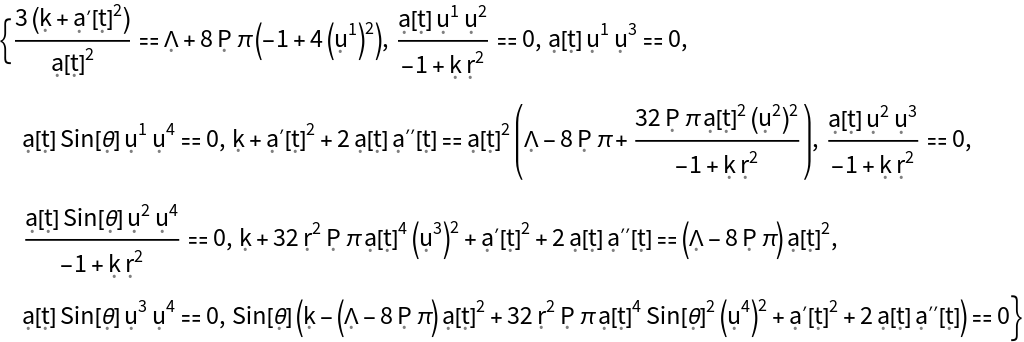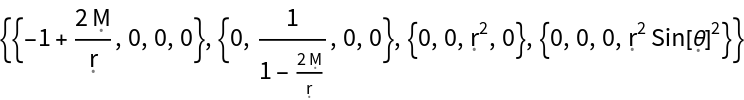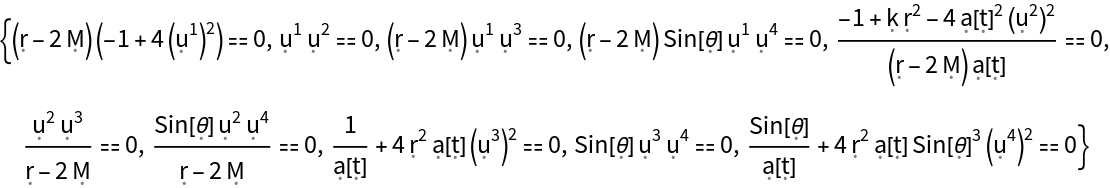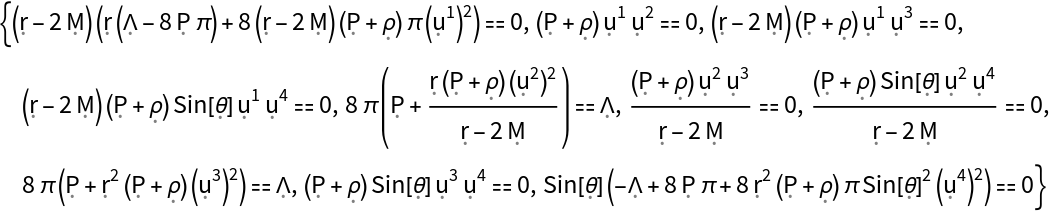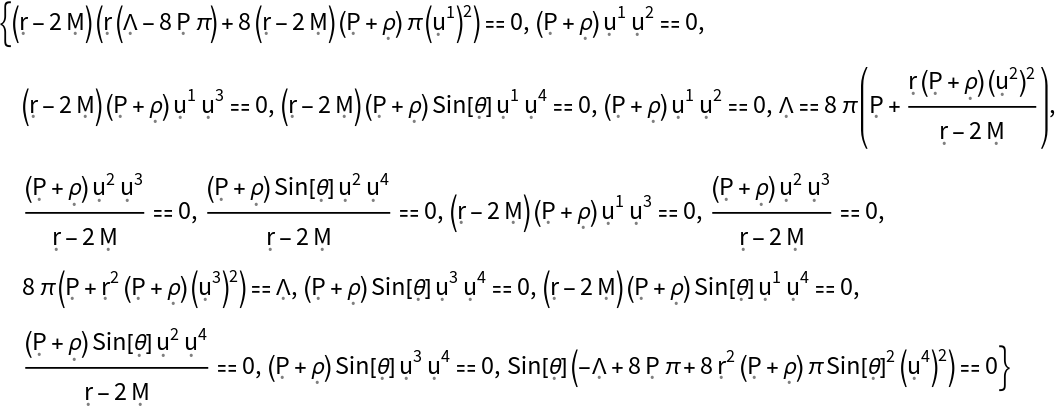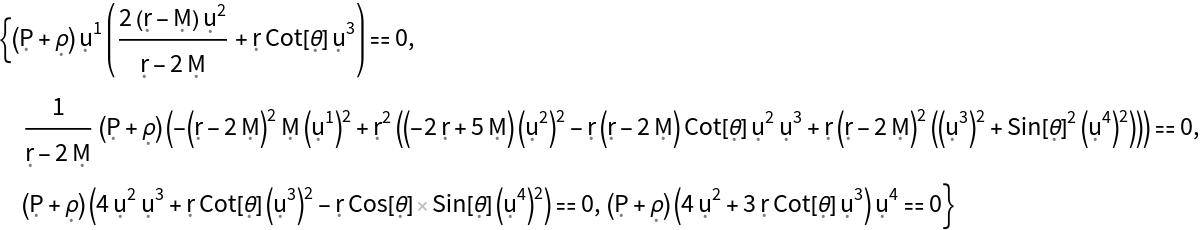Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SolveEinsteinEquations

Source Notebook

Determine whether a given stress-energy tensor (field) is a solution to the Einstein field equations

Contributed by: Jonathan Gorard

ResourceFunction["SolveEinsteinEquations"][StressEnergyTensor[…],cosmo]

attempts to solve the Einstein field equations for the given StressEnergyTensor, assuming cosmological constant cosmo.

ResourceFunction["SolveEinsteinEquations"][StressEnergyTensor[…]]

uses the default (symbolic) value as the cosmological constant.

ResourceFunction["SolveEinsteinEquations"][StressEnergyTensor[…],MetricTensor[…],cosmo]

attempts to solve the Einstein field equations for the given StressEnergyTensor, after replacing its underlying metric with the given MetricTensor, assuming cosmological constant cosmo.

ResourceFunction["SolveEinsteinEquations"][StressEnergyTensor[…],MetricTensor[…]]

replaces the underlying metric with the given MetricTensor, and uses the default (symbolic) value as the cosmological constant.

Details

The full Einstein field equations assert that the Einstein curvature tensor (or, more generally, the Einstein curvature tensor plus the metric tensor multiplied by a non-zero cosmological constant) is equal to the stress-energy tensor, at least up to a multiplicative constant. Informally, the Einstein field equations therefore relate the geometry of a spacetime/manifold (as represented by the Einstein curvature tensor) to its mass-energy content (as represented by the stress-energy tensor) in a highly explicit way.
The existence of a non-zero stress-energy tensor indicates the presence of matter fields/non-gravitational fields in spacetime (thus distinguishing the full Einstein field equations from the vacuum Einstein field equations). The vanishing of the covariant divergence of the Einstein curvature tensor, as guaranteed geometrically by the (contracted) Bianchi identities, hence guarantees the vanishing of the covariant divergence of the stress-energy tensor, which is equivalent to the statement that energy and momentum are conserved identically.
ResourceFunction["SolveEinsteinEquations"] assumes a non-zero cosmological constant (represented by the purely symbolic value ) by default, although this can be overridden as part of the second (or third) argument of the function.
ResourceFunction["SolveEinsteinEquations"] classifies all solutions to the Einstein field equations as either exact (i.e. no additional assumptions required) or non-exact (i.e. some additional assumptions required), depending upon whether any additional field equations must be assumed in order for the given StressEnergyTensor to constitute a valid solution to the full Einstein field equations. Any such field equations (if they exist) can be computed using the property "FieldEquations".
ResourceFunction["SolveEinsteinEquations"] does not assume any particular number of dimensions, nor any particular metric convention, for the underlying manifold (although some properties, such as "LorentzianConditions", implicitly assume a (-,+,+,+,…) signature). ResourceFunction["SolveEinsteinEquations"] also does not require the metric to be strictly symmetric (i.e. spin and torsion connections are supported), nor does it require the stress-energy tensor to be strictly symmetric (i.e. non-zero spin tensors are supported), although many computations implicitly assume the torsion-free Levi-Civita connection by default.
ResourceFunction["SolveEinsteinEquations"] implicitly keeps track of all known algebraic equivalences between tensor expressions, and can apply them for simplification purposes where necessary. Requesting any property with "Reduced" in its name has the effect of applying all known tensor equivalences and simplifying (note that this can have the effect of increasing computation time significantly).
By default, ResourceFunction["SolveEinsteinEquations"] evaluates all partial derivatives of the metric and stress-energy tensors automatically. In certain cases, however, these partial derivatives may be difficult or even impossible to compute, in which case the evaluation may not terminate in a reasonable time. Requesting any property with "Symbolic" in its name has the effect of leaving all partial derivatives unevaluated instead (note that this can have the effect of increasing expression length significantly).
If ResourceFunction["SolveEinsteinEquations"] succeeds in solving the full Einstein field equations (or in proving that no such solution can exist), it will return an EinsteinSolution expression.
Based on the eigenvalues of the matrix representation of the underlying metric tensor in covariant form, the underlying manifold will be classified by ResourceFunction["SolveEinsteinEquations"] as either Riemannian (all eigenvalues positive or all eigenvalues negative), pseudo-Riemannian (some eigenvalues positive and some eigenvalues negative), Lorentzian (all eigenvalues positive except for one negative, or all eigenvalues negative except for one positive) or Indeterminate.
The property "RiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation of the underlying metric tensor are strictly positive; "PseudoRiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation of the underlying metric tensor are all non-zero; "LorentzianConditions" returns the conditions necessary to guarantee that the eigenvalue corresponding to the {1,0,0,…} eigenvector of the metric tensor (if it exists) is negative, with all other eigenvalues being positive. Note that this is strictly less general than the behavior of properties such as "RiemannianQ" (described in the point above), since it assumes certain features of the metric signature.
In EinsteinSolution, the following properties are supported:
"FieldEquations"list of any (additional) field equations that must be assumed in order for the stress-energy tensor to be a valid solution to the full Einstein field equations
"EinsteinEquations"list of full Einstein field equations asserting that the Einstein tensor (plus the metric tensor multiplied by the cosmological constant) is equal to the stress-energy tensor up to a multiplicative constant
"ReducedEinsteinEquations"list of full Einstein field equations asserting that the Einstein tensor (plus the metric tensor multiplied by the cosmological constant) is equal to the stress-energy tensor up to a multiplicative constant, modulo all tensor equivalences
"SymbolicEinsteinEquations"list of full Einstein field equations asserting that the Einstein tensor (plus the metric tensor multiplied by the cosmological constant) is equal to the stress-energy tensor up to a multiplicative constant, with purely symbolic partial derivative operators
"ContinuityEquations"list of continuity equations asserting that the covariant divergence of the stress-energy tensor vanishes (i.e. energy and momentum are conserved)
"ReducedContinuityEquations"list of continuity equations asserting that the covariant divergence of the stress-energy tensor vanishes (i.e. energy and momentum are conserved), modulo all tensor equivalences
"SymbolicContinuityEquations"list of continuity equations asserting that the covariant divergence of the stress-energy tensor vanishes (i.e. energy and momentum are conserved), with purely symbolic partial derivative operators
"MetricTensor"underlying metric tensor associated to the solution of the Einstein field equations
"StressEnergyTensor"underlying stress-energy tensor associated to the solution of the Einstein field equations
"Coordinates"list of coordinate symbols for the solution of the Einstein field equations
"CoordinateOneForms"list of differential 1-form symbols for the coordinates of the solution of the Einstein field equations
"SolutionQ"whether the stress-energy tensor is a valid solution to the full Einstein field equations
"ExactSolutionQ"whether the stress-energy tensor is a valid exact solution to the full Einstein field equations (i.e. no additional field equations need to be assumed)
"CosmologicalConstant"value of the cosmological constant for the solution of the Einstein field equations
"Dimensions"number of dimensions of the underlying manifold/spacetime described by the solution of the Einstein field equations
"Signature"list of +1s and -1s designating the signature of the underlying manifold described by the solution of the Einstein field equations (+1 for each positive eigenvalue of the metric, -1 for each negative eigenavlue of the metric)
"RiemannianQ"whether the underlying manifold described by the solution of the Einstein field equations is Riemannian (i.e. all eigenvalues of the metric have the same sign)
"PseudoRiemannianQ"whether the underlying manifold described by the solution of the Einstein field equations is pseudo-Riemannian (i.e. all eigenvalues of the metric are non-zero, but not all have the same sign)
"LorentzianQ"whether the underlying manifold described by the solution of the Einstein field equations is Lorentzian (i.e. all eigenvalues of the metric have the same sign, except for one eigenvalue which has the opposite sign)
"RiemannianConditions"list of conditions required to guarantee that the underlying manifold described by the solution of the Einstein field equations is Riemannian (i.e. all eigenvalues of the metric are positive)
"PseudoRiemannianConditions"list of conditions required to guarantee that the underlying manifold described by the solution of the Einstein field equations is pseudo-Riemannian (i.e. all eigenvalues of the metric are non-zero)
"LorentzianConditions"list of conditions required to guarantee that the underlying manifold described by the solution of the Einstein field equations is Lorentzian (i.e. the "time" eigenvalue of the metric is negative and all other eigenvalues are positive)
"Properties"list of properties

Examples

Basic Examples (3) 

Solve an Einstein equation system:

In[1]:=
metric = ResourceFunction["MetricTensor"]["FLRW"]
Out[1]=

More specifically, show that a perfect and static relativistic fluid (with symbolic 4-velocity u, symbolic density and symbolic pressure P) is a valid solution to the Einstein field equations for the Friedmann-Lemaître-Robertson-Walker (FLRW) metric (for a homogeneous, isotropic and uniformly-expanding/contracting universe, with symbolic curvature parameter k and symbolic scale factor a) in standard spherical polar coordinates, with zero cosmological constant:

In[2]:=
stressEnergy = ResourceFunction["StressEnergyTensor"]["PerfectFluid", metric]
Out[2]=
In[3]:=
solution = ResourceFunction["SolveEinsteinEquations"][stressEnergy, 0]
Out[3]=
In[4]:=
solution["SolutionQ"]
Out[4]=

Show that the perfect and static relativistic fluid solution for the FLRW metric is not exact (i.e. additional field equations need to be assumed):

In[5]:=
solution["ExactSolutionQ"]
Out[5]=
In[6]:=
solution["FieldEquations"]
Out[6]=

Show that the perfect and static relativistic fluid solution for the FLRW metric remains valid when assuming a non-zero (symbolic) cosmological constant :

In[7]:=
solution2 = ResourceFunction["SolveEinsteinEquations"][stressEnergy]
Out[7]=
In[8]:=
solution2["SolutionQ"]
Out[8]=
In[9]:=
solution2["FieldEquations"]
Out[9]=

Show the list of all continuity equations for a perfect and static relativistic fluid in the FLRW geometry, asserting that energy and momentum are conserved (i.e. the covariant divergence of the stress-energy tensor vanishes):

In[10]:=
solution2["ContinuityEquations"]
Out[10]=

Show the list of all continuity equations for a perfect and static relativistic fluid in the FLRW geometry, asserting that energy and momentum are conserved (i.e. the covariant divergence of the stress-energy tensor vanishes), with all algebraic equivalences imposed:

In[11]:=
solution2["ReducedContinuityEquations"]
Out[11]=

Show that the perfect and static relativistic fluid solution for the FLRW metric remains valid when assuming a numerical 4-velocity {-1,0,0,0} (i.e. a vanishing fluid velocity):

In[12]:=
stressEnergy2 = ResourceFunction[ "StressEnergyTensor"][{"PerfectFluid", {-1, 0, 0, 0}}, metric]
Out[12]=
In[13]:=
solution3 = ResourceFunction["SolveEinsteinEquations"][stressEnergy2, 0]
Out[13]=
In[14]:=
solution3["SolutionQ"]
Out[14]=
In[15]:=
solution3["FieldEquations"]
Out[15]=

Show list of all Einstein field equations, asserting that the Einstein curvature tensor for the FLRW geometry is equal to the stress-energy tensor for a perfect and static relativistic fluid (up to a multiplicative constant):

In[16]:=
solution3["EinsteinEquations"]
Out[16]=

Show the list of all Einstein field equations, asserting that the Einstein curvature tensor for the FLRW geometry is equal to the stress-energy tensor for a perfect and static relativistic fluid (up to a multiplicative constant), with all algebraic equivalences imposed:

In[17]:=
solution3["ReducedEinsteinEquations"]
Out[17]=

Show that a static relativistic radiation distribution (i.e. a static perfect fluid whose density is equal to three times its pressure) is also a valid solution to the Einstein field equations for the FLRW metric:

In[18]:=
stressEnergy3 = ResourceFunction["StressEnergyTensor"]["Radiation", metric]
Out[18]=
In[19]:=
solution4 = ResourceFunction["SolveEinsteinEquations"][stressEnergy3, 0]
Out[19]=
In[20]:=
solution4["SolutionQ"]
Out[20]=
In[21]:=
solution4["FieldEquations"]
Out[21]=

Show that a static relativistic dust (i.e. a static perfect fluid with symbolic 4-velocity u, symbolic density and vanishing pressure) is a valid solution to the Einstein field equations for the Gödel metric (for a rotating, dust-filled universe, with symbolic angular velocity ) in Gödel’s Cartesian-like coordinates, with zero cosmological constant:

In[22]:=
metric = ResourceFunction["MetricTensor"]["Godel"]
Out[22]=
In[23]:=
stressEnergy = ResourceFunction["StressEnergyTensor"]["Dust", metric]
Out[23]=
In[24]:=
solution = ResourceFunction["SolveEinsteinEquations"][stressEnergy, 0]
Out[24]=
In[25]:=
solution["SolutionQ"]
Out[25]=

Show that the static relativistic dust solution for the Gödel metric is not exact:

In[26]:=
solution["ExactSolutionQ"]
Out[26]=
In[27]:=
solution["FieldEquations"]
Out[27]=

Show the list of all Einstein field equations asserting that the Einstein curvature tensor for the Gödel geometry is equal to the stress-energy tensor for a static relativistic dust (up to a multiplicative constant):

In[28]:=
solution["EinsteinEquations"]
Out[28]=

Show the list of all continuity equations for a static relativistic dust in the Gödel geometry, asserting that energy and momentum are conserved (i.e. the covariant divergence of the stress-energy tensor vanishes):

In[29]:=
solution["ContinuityEquations"]
Out[29]=

Show the list of all continuity equations for a static relativistic dust in the Gödel geometry, asserting that energy and momentum are conserved (i.e. the covariant divergence of the stress-energy tensor vanishes), with all algebraic equivalences imposed:

In[30]:=
solution["ReducedContinuityEquations"]
Out[30]=

Show that the static relativistic dust solution for the Gödel metric remains valid when assuming a non-zero (symbolic) cosmological constant :

In[31]:=
solution2 = ResourceFunction["SolveEinsteinEquations"][stressEnergy]
Out[31]=
In[32]:=
solution2["SolutionQ"]
Out[32]=
In[33]:=
solution2["FieldEquations"]
Out[33]=

Show that a dynamic relativistic dust distribution (i.e. a dynamic perfect fluid with symbolic 4-velocity function u, symbolic density function and vanishing pressure) is also a valid solution to the Einstein field equations for the Gödel metric:

In[34]:=
stressEnergy2 = ResourceFunction["StressEnergyTensor"]["DustField", metric]
Out[34]=
In[35]:=
solution3 = ResourceFunction["SolveEinsteinEquations"][stressEnergy2, 0]
Out[35]=
In[36]:=
solution3["SolutionQ"]
Out[36]=
In[37]:=
solution3["FieldEquations"]
Out[37]=

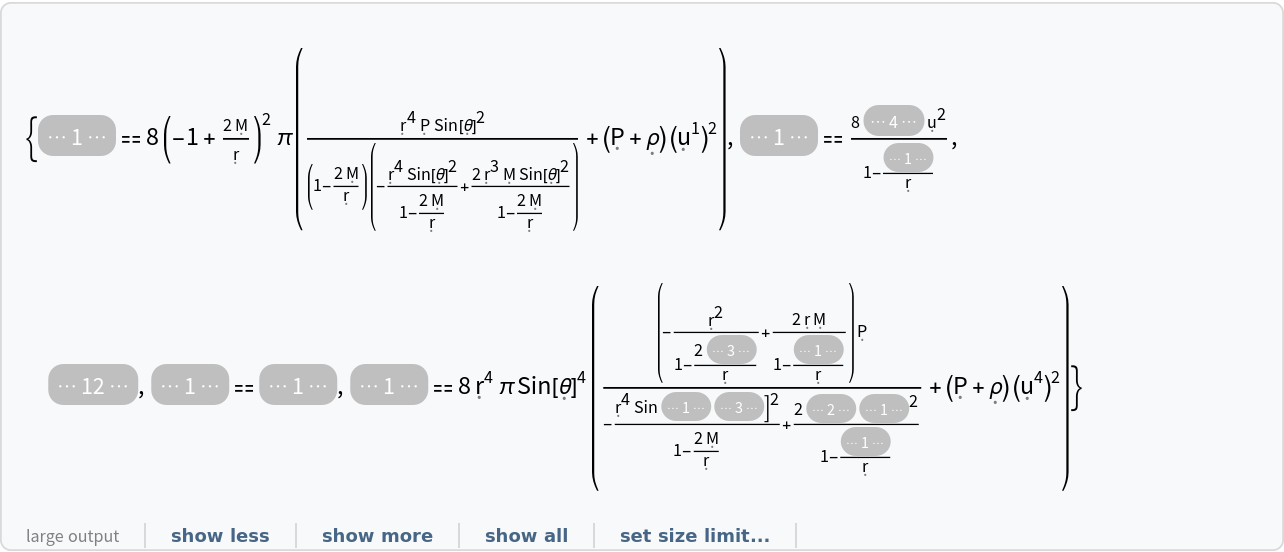
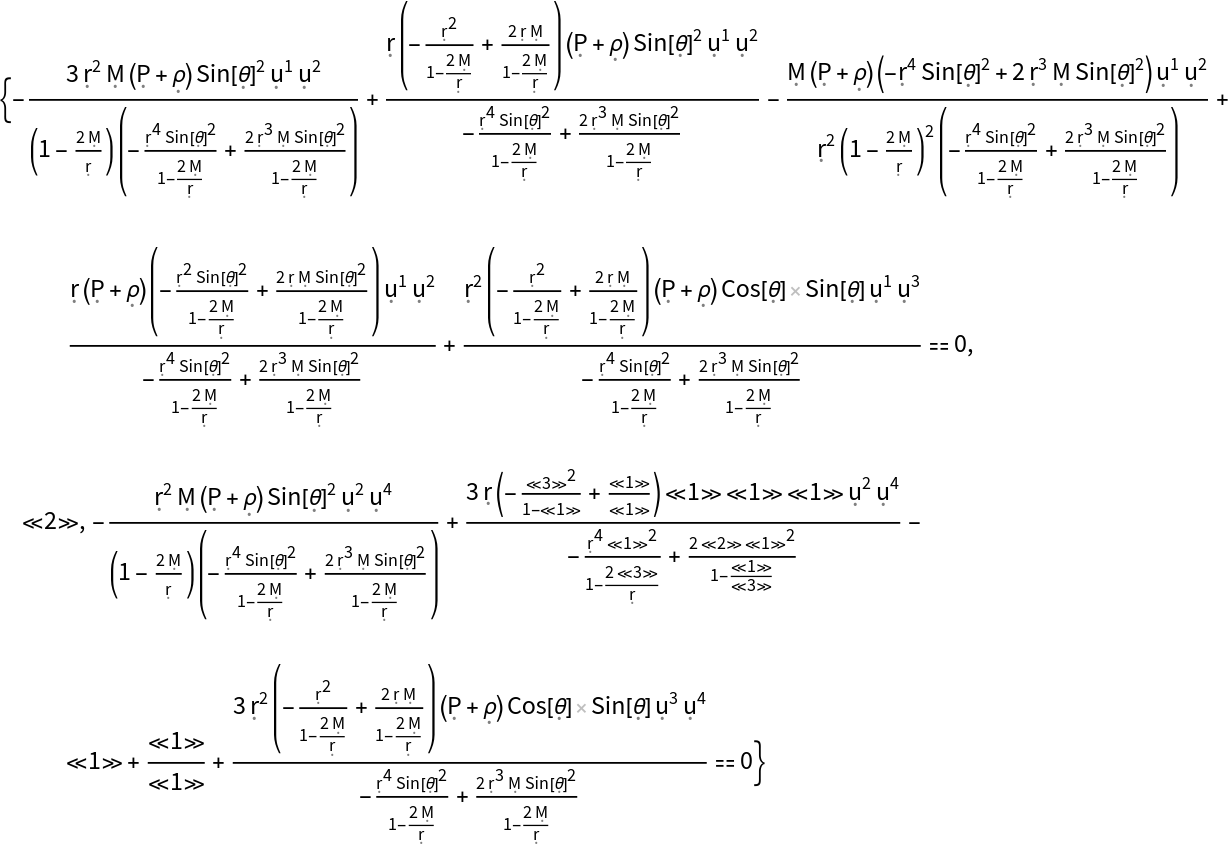
Show that a dynamic and source-free electromagnetic field (with electric scalar potential ϕ, vanishing magnetic vector potential and symbolic vacuum magnetic permeability constant 0) is a valid solution to the Einstein field equations for the Reissner-Nordström metric (for a charged, non-rotating black hole with symbolic mass M and symbolic electric charge Q) in standard spherical polar coordinates, with zero cosmological constant:

In[38]:=
metric = ResourceFunction["MetricTensor"]["ReissnerNordstrom"]
Out[38]=
In[39]:=
stressEnergy = ResourceFunction[ "StressEnergyTensor"][{"ElectromagneticField", {\[Phi], 0, 0, 0}}, metric]
Out[39]=
In[40]:=
solution = ResourceFunction["SolveEinsteinEquations"][stressEnergy, 0]
Out[40]=
In[41]:=
solution["SolutionQ"]
Out[41]=
In[42]:=
solution["FieldEquations"]
Out[42]=

Show that the dynamic and source-free electromagnetic field solution for the Reissner-Nordström metric remains valid when assuming a non-zero (symbolic) cosmological constant :

In[43]:=
solution2 = ResourceFunction["SolveEinsteinEquations"][stressEnergy]
Out[43]=
In[44]:=
solution2["SolutionQ"]
Out[44]=
In[45]:=
solution2["FieldEquations"]
Out[45]=

Scope (3) 

By default, SolveEinsteinEquations will solve the Einstein field equations in terms of the MetricTensor associated to the given StressEnergyTensor:

In[46]:=
stressEnergy = ResourceFunction["StressEnergyTensor"]["Dust", ResourceFunction["MetricTensor"]["FLRW"]]
Out[46]=
In[47]:=
solution = ResourceFunction["SolveEinsteinEquations"][stressEnergy]
Out[47]=
In[48]:=
solution["MetricTensor"]["MatrixRepresentation"]
Out[48]=
In[49]:=
solution["FieldEquations"]
Out[49]=

This default choice may be overridden using an additional argument:

In[50]:=
solution2 = ResourceFunction["SolveEinsteinEquations"][stressEnergy, ResourceFunction["MetricTensor"]["Schwarzschild"]]
Out[50]=
In[51]:=
solution2["MetricTensor"]["MatrixRepresentation"]
Out[51]=
In[52]:=
solution2["FieldEquations"]
Out[52]=

By default, SolveEinsteinEquations will use a symbolic value () for the cosmological constant:

In[53]:=
stressEnergy = ResourceFunction["StressEnergyTensor"]["Radiation", ResourceFunction["MetricTensor"]["FLRW"]]
Out[53]=
In[54]:=
solution = ResourceFunction["SolveEinsteinEquations"][stressEnergy]
Out[54]=
In[55]:=
solution["CosmologicalConstant"]
Out[55]=
In[56]:=
solution["FieldEquations"]
Out[56]=

This default choice may be overridden using an additional argument:

In[57]:=
solution2 = ResourceFunction["SolveEinsteinEquations"][stressEnergy, 0]
Out[57]=
In[58]:=
solution2["CosmologicalConstant"]
Out[58]=
In[59]:=
solution2["FieldEquations"]
Out[59]=

The MetricTensor and cosmological constant arguments can be specified simultaneously:

In[60]:=
solution3 = ResourceFunction["SolveEinsteinEquations"][stressEnergy, ResourceFunction["MetricTensor"]["Schwarzschild"], 0]
Out[60]=
In[61]:=
solution3["MetricTensor"]["MatrixRepresentation"]
Out[61]=
In[62]:=
solution3["CosmologicalConstant"]
Out[62]=
In[63]:=
solution3["FieldEquations"]
Out[63]=

Solve the full Einstein field equations for a perfect and static relativistic fluid (with symbolic 4-velocity u, symbolic density and symbolic pressure P) in the Schwarzschild metric, with symbolic mass M, and assuming symbolic cosmological constant :

In[64]:=
stressEnergy = ResourceFunction["StressEnergyTensor"]["PerfectFluid", ResourceFunction["MetricTensor"]["Schwarzschild"]]
Out[64]=
In[65]:=
solution = ResourceFunction["SolveEinsteinEquations"][stressEnergy]
Out[65]=

Show the list of properties:

In[66]:=
solution["Properties"]
Out[66]=

Show the list of (additional) field equations that must be assumed in order for the stress-energy tensor to be a valid solution to the full Einstein field equations:

In[67]:=
solution["FieldEquations"]
Out[67]=

Show the list of full Einstein field equations asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) is equal to the stress-energy tensor up to a multiplicative constant:

In[68]:=
solution["EinsteinEquations"]
Out[68]=

Show the list of full Einstein field equations asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) is equal to the stress-energy tensor up to a multiplicative constant, with all algebraic equivalences imposed:

In[69]:=
solution["ReducedEinsteinEquations"]
Out[69]=

Show the list of full Einstein field equations asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) is equal to the stress-energy tensor up to a multiplicative constant, with all partial derivative operators left purely symbolic:

In[70]:=
solution["SymbolicEinsteinEquations"]
Out[70]=

Show the list of all continuity equations asserting that the covariant divergence of the stress-energy tensor must vanish (i.e. energy and momentum are conserved):

In[71]:=
Short[solution["ContinuityEquations"], 12]
Out[71]=

Show the list of all continuity equations asserting that the covariant divergence of the stress-energy tensor must vanish (i.e. energy and momentum are conserved), with all algebraic equivalences imposed:

In[72]:=
solution["ReducedContinuityEquations"]
Out[72]=

Show the list of all continuity equations asserting that the covariant divergence of the stress-energy tensor must vanish (i.e. energy and momentum are conserved), with all partial derivative operators left purely symbolic:

In[73]:=
Short[solution["SymbolicContinuityEquations"], 12]
Out[73]=

Show the metric tensor for the underlying manifold represented by the solution of the full Einstein field equations:

In[74]:=
solution["MetricTensor"]
Out[74]=

Show the stress-energy tensor associated to the solution of the full Einstein field equations:

In[75]:=
solution["StressEnergyTensor"]
Out[75]=

Show the list of coordinate symbols for the solution of the full Einstein field equations:

In[76]:=
solution["Coordinates"]
Out[76]=

Show the list of differential 1-form symbols for the coordinates of the solution of the full Einstein field equations:

In[77]:=
solution["CoordinateOneForms"]
Out[77]=

Determine whether the stress-energy tensor is a valid solution of the full Einstein field equations:

In[78]:=
solution["SolutionQ"]
Out[78]=

Determine whether the stress-energy tensor is a valid exact solution to the full Einstein field equations (i.e. no additional field equations need to be assumed):

In[79]:=
solution["ExactSolutionQ"]
Out[79]=

Show the value of the cosmological constant for the solution of the full Einstein field equations:

In[80]:=
solution["CosmologicalConstant"]
Out[80]=

Show the number of dimensions of the underlying manifold represented by the solution of the full Einstein field equations:

In[81]:=
solution["Dimensions"]
Out[81]=

Show the signature of the underlying manifold represented by the solution of the full Einstein field equations (with +1s representing positive eigenvalues and -1s representing negative eigenvalues of the metric tensor):

In[82]:=
solution["Signature"]
Out[82]=

Determine whether the underlying manifold represented by the solution of the full Einstein field equations is Riemannian (i.e. all eigenvalues of the metric tensor have the same sign):

In[83]:=
solution["RiemannianQ"]
Out[83]=

Determine whether the underlying manifold represented by the solution of the full Einstein field equations is pseudo-Riemannian (i.e. all eigenvalues are non-zero, but not all have the same sign):

In[84]:=
solution["PseudoRiemannianQ"]
Out[84]=

Determine whether the underlying manifold represented by the solution of the full Einstein field equations is Lorentzian (i.e. all eigenvalues of the metric tensor have the same sign, except for one eigenvalue which has the opposite sign):

In[85]:=
solution["LorentzianQ"]
Out[85]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the solution of the full Einstein field equations is Riemannian (i.e. all eigenvalues of the metric tensor are positive):

In[86]:=
solution["RiemannianConditions"]
Out[86]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the solution of the full Einstein field equations is pseudo-Riemannian (i.e. all eigenvalues of the metric tensor are non-zero):

In[87]:=
solution["PseudoRiemannianConditions"]
Out[87]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the solution of the full Einstein field equations is Lorentzian (i.e. the "time" eigenvalue is negative, and all other eigenvalues are positive):

In[88]:=
solution["LorentzianConditions"]
Out[88]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 24 July 2023

Source Metadata

  • Citation:
    • Charles W. Misner, Kip S. Thorne and John Archibald Wheeler (1973), Gravitation
    • Stephen Wolfram (2002), A New Kind of Science
    • Stephen Wolfram (2020), "A Class of Models with Potential to Represent Fundamental Physics"
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

License Information