Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SolarSystemMandala

Source Notebook

Create intricate emergent patterns by connecting the positions of planets over a range of dates

Contributed by: Jeff Bryant

ResourceFunction["SolarSystemMandala"][entity,period,incr]

generates a mandala plotting a single line along the path of entity over period with stepsize incr.

ResourceFunction["SolarSystemMandala"][entity1,entity2,period,incr]

generates a mandala plotting lines between entity1 and entity2.

Details and Options

SolarSystemMandala["AllowedEntities"] returns a list of supported entities.
SolarSystemMandala takes the same options as Graphics in addition to the following options:
AstroReferenceFrame"Ecliptic"observation data (frame, date, location, …)
"LineColors"{ColorData[106,6]}one or more colors to use for lines
"LineOpacity"1opacity value to apply to lines
"StartDate"Nowdate for the mandala to start from

Examples

Basic Examples (2) 

Compute a mandala of Mars as observed from Earth in the ecliptic coordinate system:

In[1]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Mars"], Quantity[20, "Years"], Quantity[.2, "Months"]]
Out[1]=

Compute a mandala using a line between Venus and Mercury over two orbits of Venus:

In[2]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Venus"], Entity["Planet", "Mercury"], 2 Entity["Planet", "Venus"]["OrbitPeriod"], Quantity[.03, "Months"]]
Out[2]=

Scope (3) 

Emergent patterns are minimal over short time spans:

In[3]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Earth"], Entity["Planet", "Mercury"], .25 Entity["Planet", "Earth"]["OrbitPeriod"], Quantity[1, "Days"]]
Out[3]=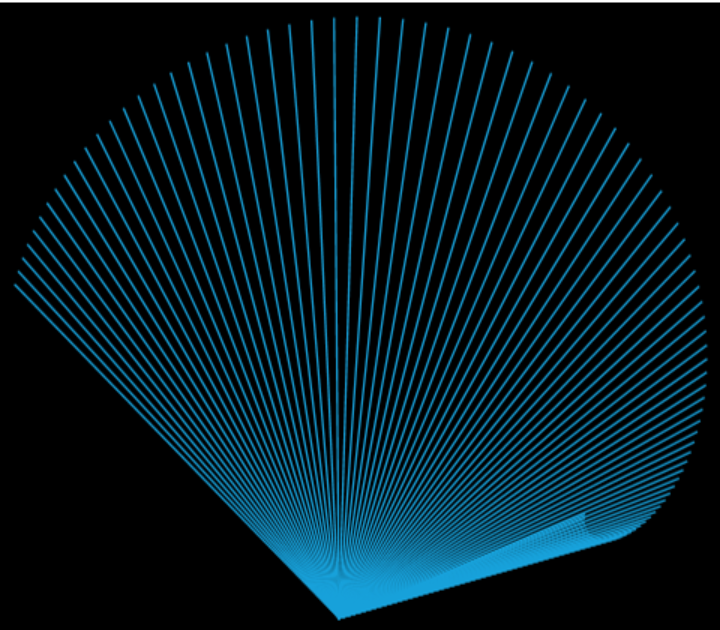

Increasing the time span reveals increasingly complex patterns:

In[4]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Earth"], Entity["Planet", "Mercury"], 1 Entity["Planet", "Earth"]["OrbitPeriod"], Quantity[1, "Days"]]
Out[4]=

Decrease the sampling frequency:

In[5]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Earth"], Entity["Planet", "Mercury"], 1 Entity["Planet", "Earth"]["OrbitPeriod"], Quantity[3, "Days"]]
Out[5]=

Options (5) 

Change the default line color:

In[6]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Mars"], Quantity[20, "Years"], Quantity[.2, "Months"], "LineColors" -> Orange]
Out[6]=

Change the reference frame to observe from the solar system barycenter:

In[7]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Earth"], Entity["Planet", "Venus"], 10 Entity["Planet", "Earth"]["OrbitPeriod"], Quantity[.5, "Months"], \!\(\* TagBox[ ButtonBox[ StyleBox["AstroReferenceFrame", "SymbolsRefLink", ShowStringCharacters->True, FontFamily->"Source Sans Pro", "NodeID" -> 30], BaseStyle->{"Link"}, ButtonData->"paclet:ref/AstroReferenceFrame", ContentPadding->False], MouseAppearanceTag["LinkHand"]]\) -> {"Ecliptic", "SSB"}]
Out[7]=

Change the reference frame along with line opacity and allow each line to vary between two colors:

In[8]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Earth"], Entity["Planet", "Venus"], 75 Entity["Planet", "Earth"]["OrbitPeriod"], Quantity[.03, "Months"], "LineOpacity" -> .01, "LineColors" -> {LightBlue, LightYellow}, AstroReferenceFrame -> {"Ecliptic", "SSB"}]
Out[8]=

Change the plot range:

In[9]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Mars"], Entity["Planet", "Venus"], 5 Entity["Planet", "Mars"]["OrbitPeriod"], Quantity[.2, "Months"], AstroReferenceFrame -> {"Ecliptic", "SSB"}, "LineOpacity" -> .5, "LineColors" -> {Darker[Red], LightBlue}, PlotRange -> 1]
Out[9]=

Observe how the pattern changes between Jupiter and Mars when using different reference frames:

In[10]:=
GraphicsGrid[{ResourceFunction["SolarSystemMandala"][ Entity["Planet", "Jupiter"], Entity["Planet", "Mars"], Entity["Planet", "Jupiter"]["OrbitPeriod"], Quantity[.05, "Months"], "LineOpacity" -> .1, "LineColors" -> {White, Darker[Red]}, AstroReferenceFrame -> #] & /@ {{"Ecliptic", "SSB"}, "Ecliptic"}}, ImageSize -> 600]
Out[10]=

Observe how the pattern changes between Jupiter and Uranus when using different reference frames:

In[11]:=
GraphicsGrid[{ResourceFunction["SolarSystemMandala"][ Entity["Planet", "Jupiter"], Entity["Planet", "Uranus"], Entity["Planet", "Uranus"]["OrbitPeriod"], Quantity[.1, "Months"], "LineOpacity" -> .01, "LineColors" -> {LightPink, LightBlue}, AstroReferenceFrame -> #] & /@ {{"Ecliptic", "SSB"}, "Ecliptic"}}, ImageSize -> 600]
Out[11]=

Observe how the pattern changes between Jupiter and Neptune when using different reference frames:

In[12]:=
GraphicsGrid[{ResourceFunction["SolarSystemMandala"][ Entity["Planet", "Jupiter"], Entity["Planet", "Neptune"], Entity["Planet", "Neptune"]["OrbitPeriod"], Quantity[.1, "Months"], "LineOpacity" -> .01, "LineColors" -> {LightPink, LightBlue}, AstroReferenceFrame -> #] & /@ {{"Ecliptic", "SSB"}, "Ecliptic"}}, ImageSize -> 600]
Out[12]=

Possible Issues (2) 

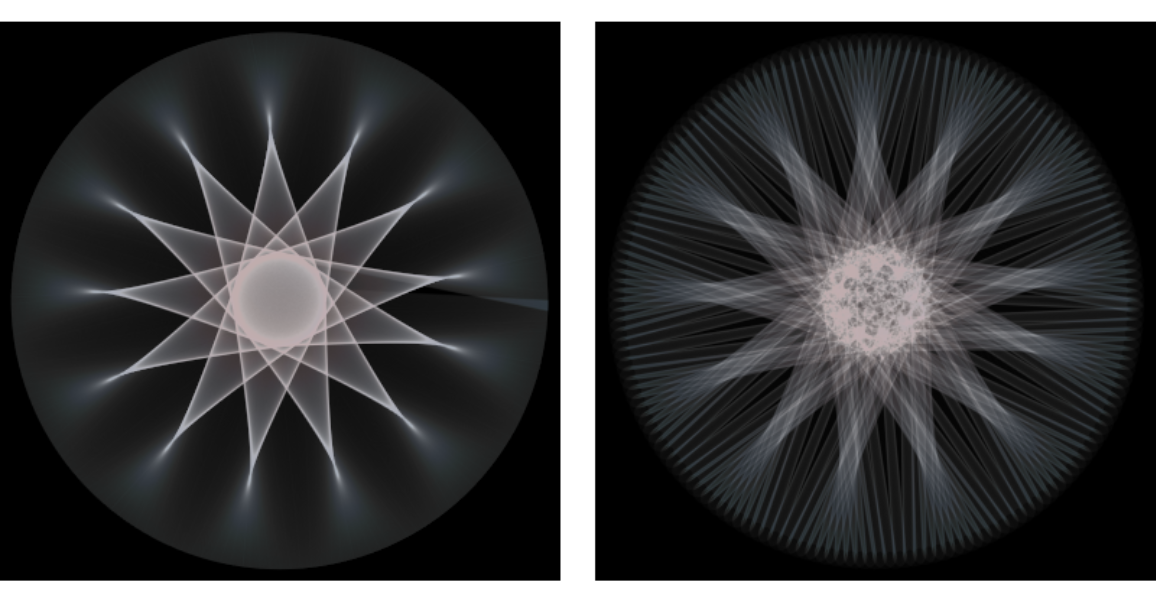Some minor planets are not supported in the far future:

In[13]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Jupiter"], Entity["MinorPlanet", "Juno"], 20 Entity["Planet", "Jupiter"]["OrbitPeriod"], Quantity[.5, "Months"], "LineOpacity" -> .1, "LineColors" -> {Pink, LightBlue}]
Out[13]=

Reducing the period avoids this problem:

In[14]:=
ResourceFunction["SolarSystemMandala"][Entity["Planet", "Jupiter"], Entity["MinorPlanet", "Juno"], 12 Entity["Planet", "Jupiter"]["OrbitPeriod"], Quantity[.5, "Months"], "LineOpacity" -> .1, "LineColors" -> {Pink, LightBlue}]
Out[14]=

Neat Examples (1) 

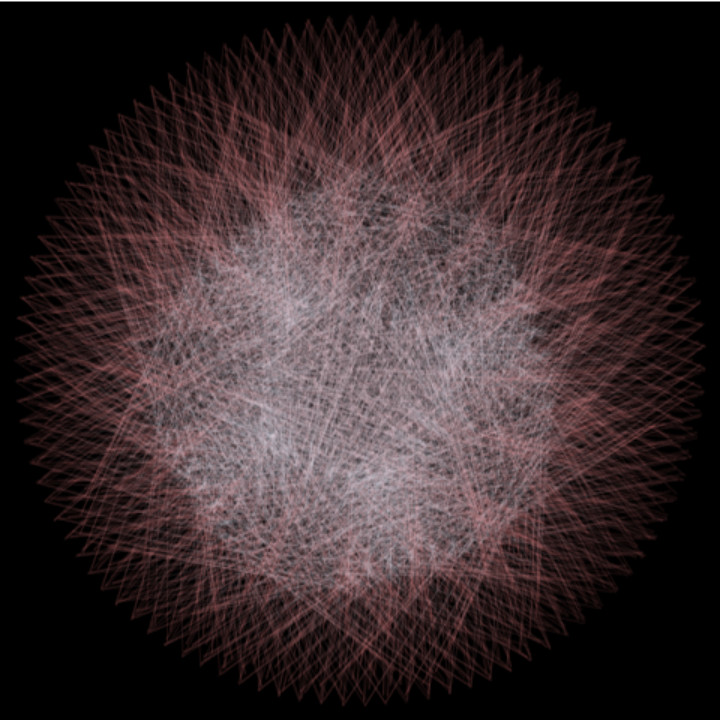Neptune and Pluto are in orbital resonance with each other which creates a unique pattern:

In[15]:=
ResourceFunction["SolarSystemMandala"][Entity["MinorPlanet", "Pluto"], Entity["Planet", "Neptune"], 20 Entity["MinorPlanet", "Pluto"]["OrbitPeriod"], Quantity[6, "Months"], "LineOpacity" -> .02, "LineColors" -> {Pink, LightBlue}, AstroReferenceFrame -> "ICRS"]
Out[15]=

Requirements

Wolfram Language 13.2 (December 2022) or above

Version History

  • 1.0.0 – 12 April 2024

Related Resources

License Information