Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
An improved sigmoidal interpolation function
ResourceFunction["SmootherStep"][x] returns a sigmoidal, Hermite interpolation between [0,1] for x on [0,1]. | |
ResourceFunction["SmootherStep"][x,{min,max}] returns a sigmoidal, Hermite interpolation between [0,1] for x on [min,max]. |
The function is sigmoidal, and inputs less than 0.5 underestimate the input:
| In[1]:= |
| Out[1]= |
Values greater than 0.5 do the opposite:
| In[2]:= |
| Out[2]= |
Plot the function:
| In[3]:= |
| Out[3]= | 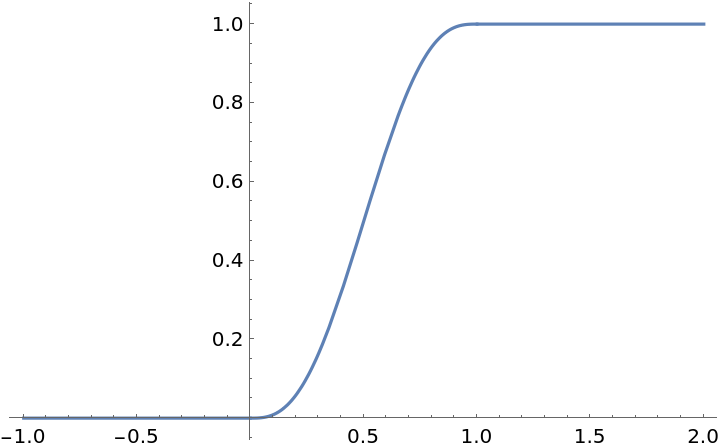 |
The single-argument form of SmootherStep passes through the point {0.5,0.5}:
| In[4]:= |
| Out[4]= |
Specify an input domain by giving a second argument:
| In[5]:= |
| Out[5]= | 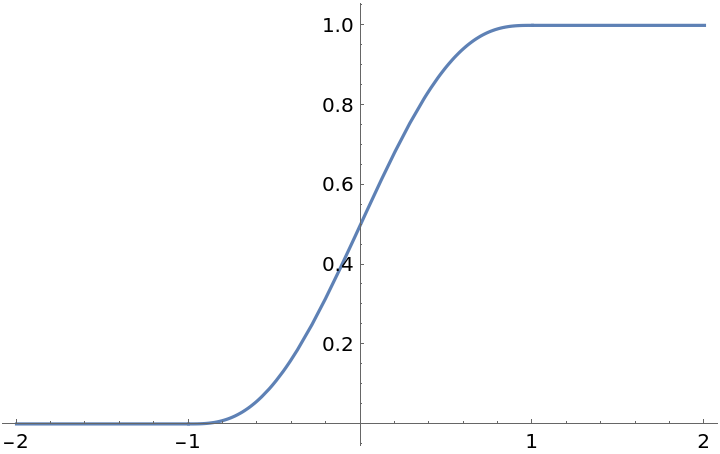 |
Smoothly interpolate with more gradual changes at the start and stop of the interpolation domain:
| In[6]:= |
| Out[6]= | 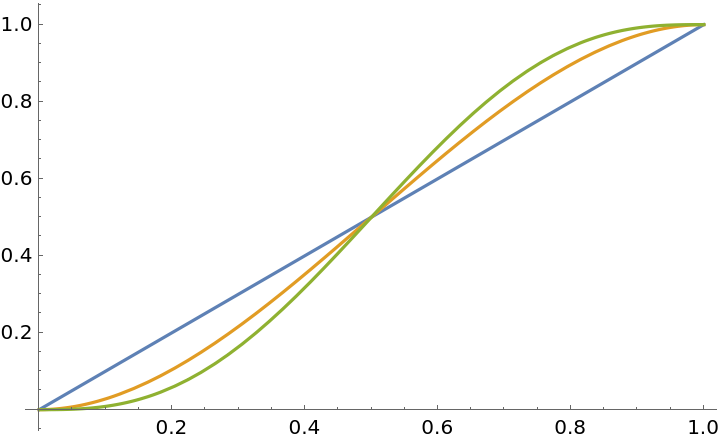 |
Interpolate colors:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
The resource function SmoothSkip is second-order discontinuous at x=0 and x=1, creating artifacts in some uses. SmootherStep addresses this:
| In[9]:= |
| Out[9]= | 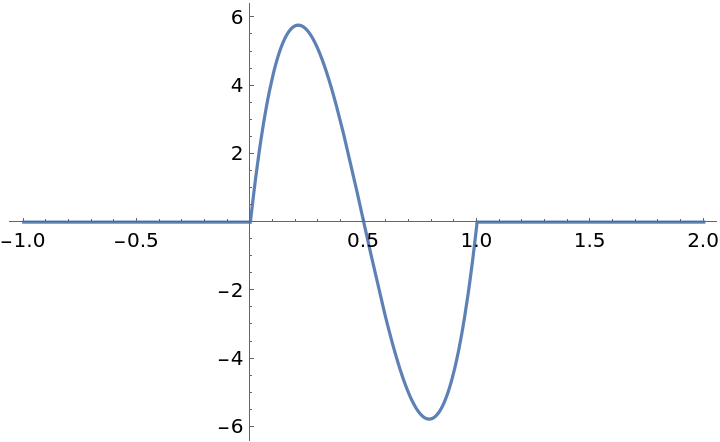 |
SmootherStep approximates the animation technique of "ease-in / ease-out":
| In[10]:= | ![Animate[Graphics[
Text["Zoom!", {ResourceFunction["SmootherStep"][x], 0}], PlotRange -> {{-.1, 1.1}, {-.1, .1}}], {x, -1, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/759/75926152-853d-40e3-a10a-12bd6801dbbe/031508e689213c0d.png) |
| Out[10]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License