Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
A sigmoidal interpolation function
ResourceFunction["SmoothStep"][x] returns a sigmoidal, Hermite interpolation between [0,1] for x on [0,1]. | |
ResourceFunction["SmoothStep"][x,{min,max}] returns a sigmoidal, Hermite interpolation between [0,1] for x on [min,max]. |
The function is sigmoidal and inputs smaller than 0.5 underestimate the input:
| In[1]:= |
| Out[1]= |
Values larger than 0.5 do the opposite:
| In[2]:= |
| Out[2]= |
Plot the function:
| In[3]:= |
| Out[3]= | 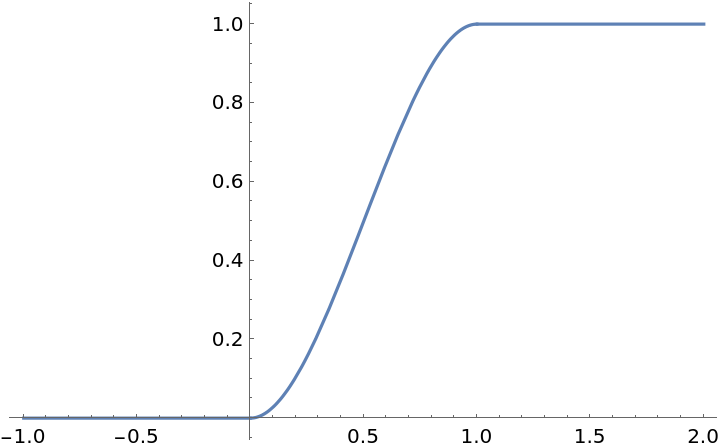 |
The single-argument form of SmoothStep passes through the point {0.5,0.5}:
| In[4]:= |
| Out[4]= |
Specify an input domain by giving a second argument:
| In[5]:= |
| Out[5]= | 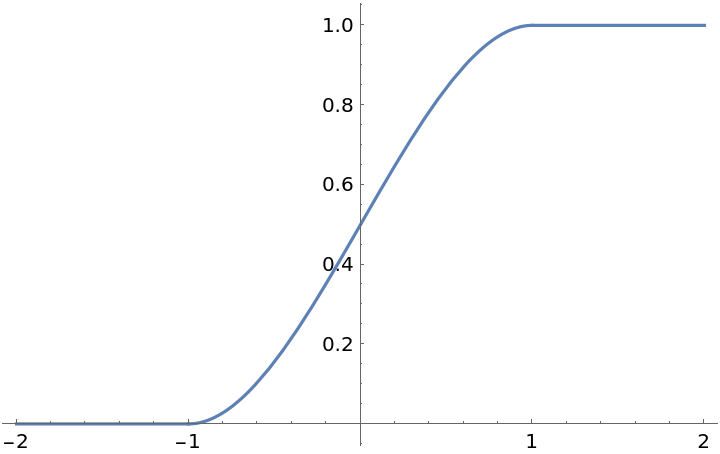 |
Smoothly interpolate with more gradual changes at the start and stop of the interpolation domain:
| In[6]:= |
| Out[6]= | 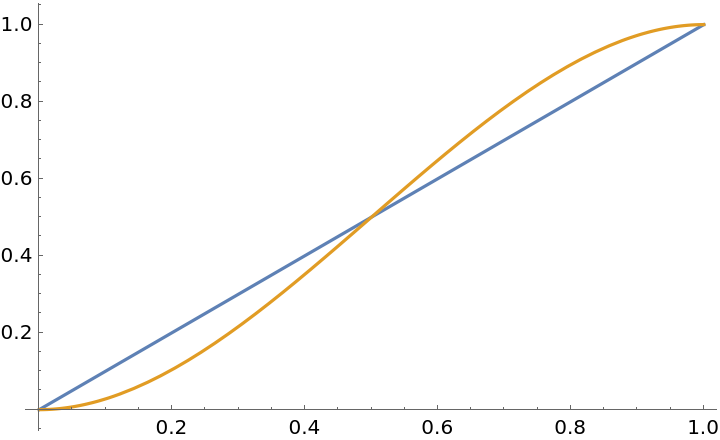 |
Interpolate colors:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
The derivative of SmoothStep approaches 0 as x approaches 0 or 1 from either side:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
SmoothStep is second-order discontinuous at x=0 and x=1:
| In[11]:= |
| Out[11]= | 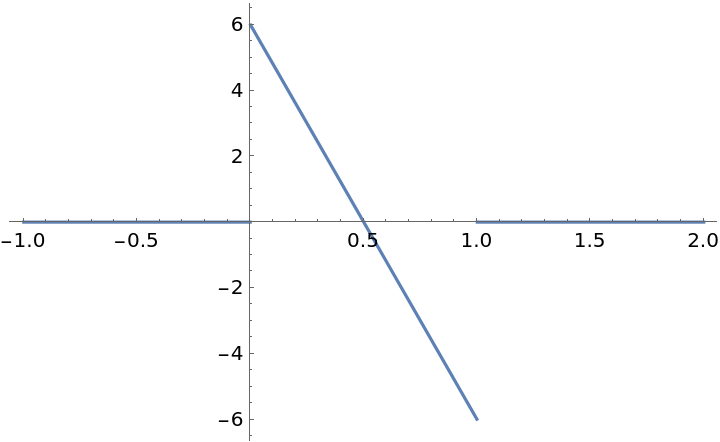 |
SmoothStep approximates the animation technique of "ease-in / ease-out":
| In[12]:= | ![Animate[Graphics[
Text["Zoom!", {ResourceFunction["SmoothStep"][x], 0}], PlotRange -> {{-.1, 1.1}, {-.1, .1}}], {x, -1, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/45e/45eab264-322e-4fa1-a68b-e14d5c3c2fb2/19ebf656e5645e4f.png) |
| Out[12]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License