Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create an animation from a list of expressions
ResourceFunction["SimpleListAnimate"][{expr1,expr2,…}] generates an animation whose frames are the successive expri. | |
ResourceFunction["SimpleListAnimate"][list,fps] displays fps frames per second. |
| Alignment | Automatic | how to align objects in the display area |
| AnimationDirection | Forward | the direction of the animation |
| AnimationRepetitions | Infinity | how many times to run before stopping |
| AnimationRunTime | 0 | time elapsed since the animation last started running, or 0 if the animation is not running |
| AnimationTimeIndex | Automatic | time index for the animation, where 0 is the beginning and the value of DefaultDuration is the end |
| DefaultDuration | 5 | the default duration in seconds |
| DisplayAllSteps | True | whether to force all expri to be displayed |
| ImageSize | All | the overall image size to use |
Animate a sequence of images:
| In[1]:= |
| Out[1]= | 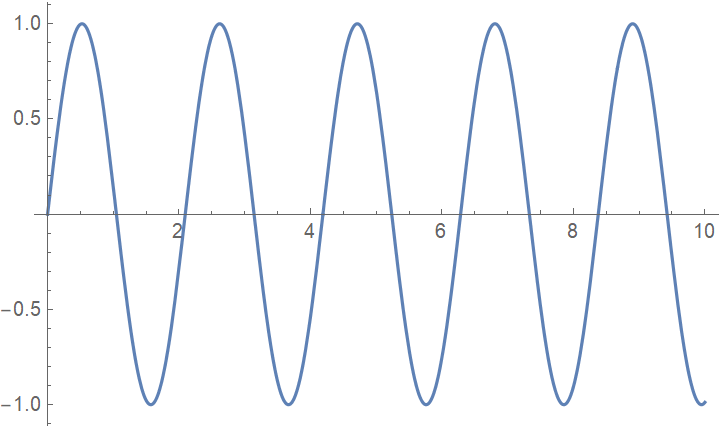 |
Create an animated bird:
| In[2]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/53c1c4f3-29e8-4ffc-9f76-e90dcfea1871"]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/43b11d19454d2deb.png) |
| Out[2]= |
Use the resource function BirdSay with the bird:
| In[3]:= |
| Out[3]= |  |
Animate a list of Wolfram Language expressions:
| In[4]:= |
| Out[4]= |
Animate a sequence of expressions:
| In[5]:= |
| Out[5]= |
Force the expressions to wrap at a fixed width:
| In[6]:= |
| Out[6]= | 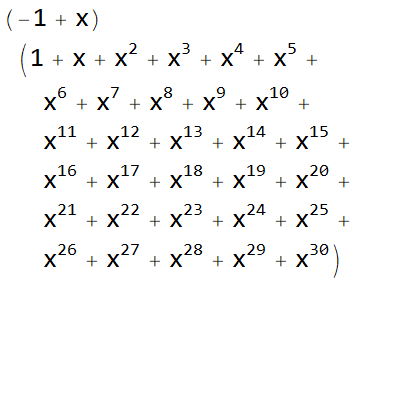 |
By default, the animation lasts a total of five seconds:
| In[7]:= |
| Out[7]= |  |
Control the display rate of each frame using a second argument:
| In[8]:= |
| Out[8]= |  |
Use preset values:
| In[9]:= | ![Table[ResourceFunction["SimpleListAnimate"][{"a", "hello world", "b"},
Alignment -> a, AnimationRunning -> False], {a, {Left, Center, Right}}]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/275bfca44ae6941c.png) |
| Out[9]= |
Control the direction of animation:
| In[10]:= | ![Table[ResourceFunction["SimpleListAnimate"][{1, 2, 3}, AnimationDirection -> a, AnimationRunning -> False], {a, {Forward, Backward, ForwardBackward}}]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/565bf8e92af2da66.png) |
| Out[10]= |
Control the animation rate:
| In[11]:= | ![Table[ResourceFunction["SimpleListAnimate"][Range[10], AnimationRate -> a, AnimationRunning -> False], {a, {0.5, 1}}]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/5e27573820caeb20.png) |
| Out[11]= |
Control the number of animation cycles:
| In[12]:= | ![Table[ResourceFunction["SimpleListAnimate"][{1, 2, 3}, AnimationRepetitions -> a, AnimationRunning -> False], {a, 1, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/0ee655415bc6da01.png) |
| Out[12]= |
By default, SimpleListAnimate starts running when evaluated:
| In[13]:= |
| Out[13]= |
By setting AnimationRunning→False, SimpleListAnimate starts in a paused state:
| In[14]:= |
| Out[14]= |
Control the time duration of one animation cycle:
| In[15]:= |
| Out[15]= |
By default, SimpleListAnimate leaves enough space for its content without ever having to resize:
| In[16]:= |
| Out[16]= |  |
By setting ImageSize, leave just enough space for the current display:
| In[17]:= |
| Out[17]= |
A fully custom image size:
| In[18]:= |
| Out[18]= |  |
Collect the individual steps in an optimization problem:
| In[19]:= |
| Out[19]= |  |
Animate the progression of the solver:
| In[20]:= | ![ResourceFunction["SimpleListAnimate"][
Table[ListLinePlot[Take[steps, i], Mesh -> All, PlotRange -> {{-1, 1.1}, {-1, 1.1}}], {i, Length[steps]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/68a7f30760bd60a1.png) |
| Out[20]= | 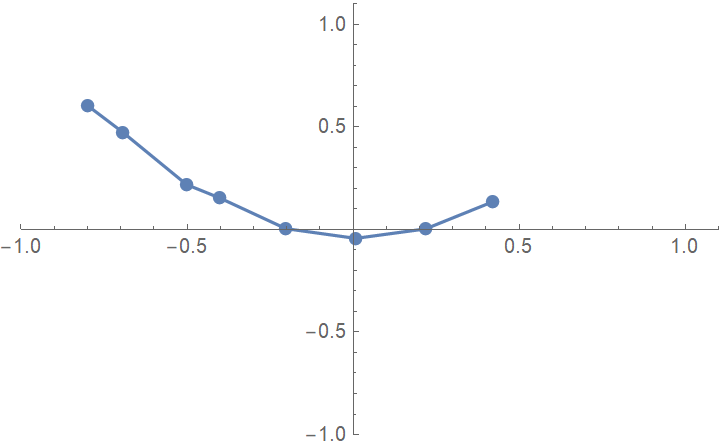 |
Collect individual steps when solving the sine-Gordon PDE:
| In[21]:= | ![{sol, {steps}} = Reap@NDSolve[{\!\(
\*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(u[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \(x, x\)]\(u[t, x]\)\) + Sin[u[t, x]] , u[0, x] == E^-x^2,
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[0, x] == 0, u[t, -10] == u[t, 10]}, u, {t, 0, 8}, {x, -10, 10}, StepMonitor :> Sow[Plot[u[t, x], {x, -10, 10}, PlotRange -> {0, 8}]]]; // Quiet](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/36da9eb3f1028a3a.png) |
Animate the solution progress:
| In[22]:= |
| Out[22]= | 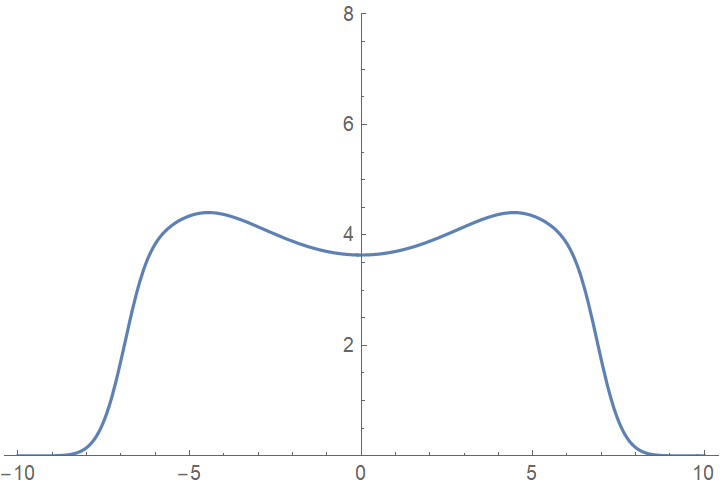 |
An implementation of LU decomposition that uses Sow on all intermediate steps:
| In[23]:= | ![LU[A_] :=
Module[{m, n, L, U}, {m, n} = Dimensions[A];
L = IdentityMatrix[n]; Sow[L, "L" ];
U = A; Sow[U, "U"];
Do[
L[[k ;; n, k]] = U[[k ;; n, k]]/U[[k, k]]; Sow[L, "L"];
U[[(k + 1) ;; n, k ;; n]] = U[[(k + 1) ;; n, k ;; n]] - L[[(k + 1) ;; n, {k}]] . U[[{k}, k ;; n]]; Sow[U, "U"];
, {k, 1, n - 1}];
{L, U}
];](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/70b26be50c61fd51.png) |
Reap the intermediate results and make an animation:
| In[24]:= | ![LUAnimate[A_, f_] :=
Module[ {lu, l, u}, {lu, {{l}, {u}}} = Reap[ LU[ A ], {"L", "U"}];
ResourceFunction["SimpleListAnimate"][
Table[Row[{f[l[[i]]], ".", f[u[[i]]], "==", f[A]}], {i, Length[l]}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/4229f5902a1b2fba.png) |
| In[25]:= |
| Out[25]= | 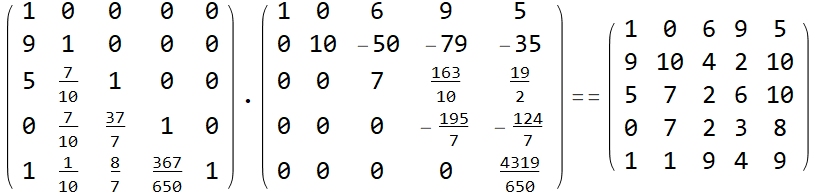 |
Use MatrixPlot for larger matrices:
| In[26]:= |
| Out[26]= | 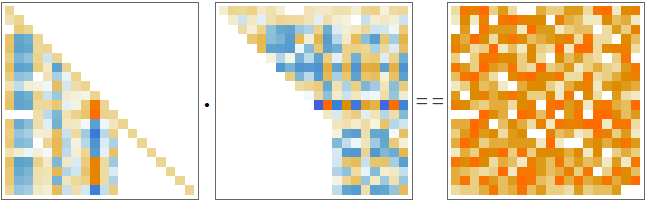 |
Show changing moon phases in a month:
| In[27]:= |
| In[28]:= |
| In[29]:= | ![list = MapThread[
Framed[Labeled[ImageResize[#1, 45], Style[#3, Bold, FontFamily -> "Helvetica"]], Background -> Lighter[ColorData["StarryNightColors", #2], .3]] &, {mp, sf, Range[Length[mp]]}];](https://www.wolframcloud.com/obj/resourcesystem/images/fa4/fa4f1a81-dd00-480d-b3d3-edf987ea2c04/7292b2f64d28efe9.png) |
| In[30]:= |
| Out[30]= |  |
Use SimpleListAnimate to animate output from Table:
| In[31]:= |
| Out[31]= | 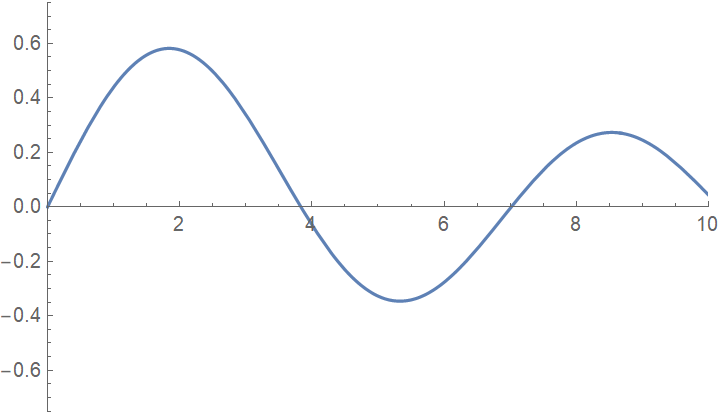 |
Use Animate for animations that depend on a parameter:
| In[32]:= |
| Out[32]= | 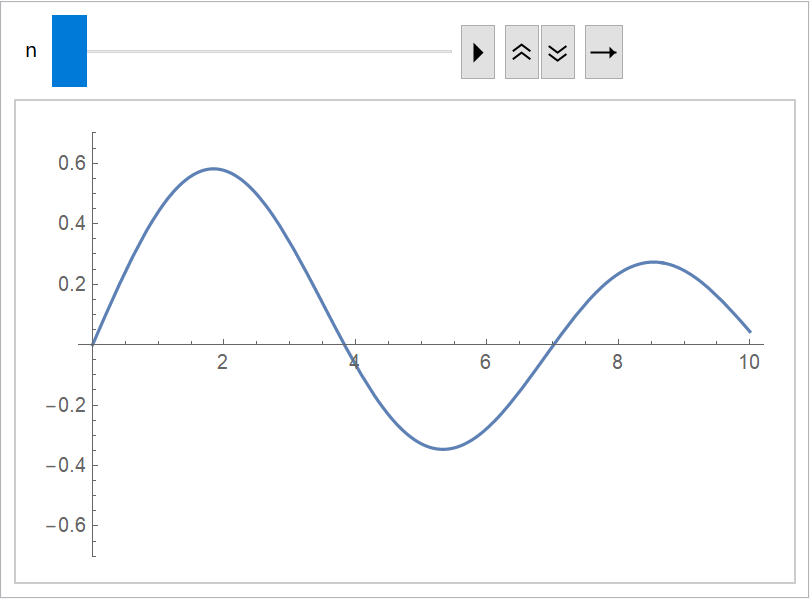 |
Use Animator when assembling a custom animation frame:
| In[33]:= |
| Out[33]= | 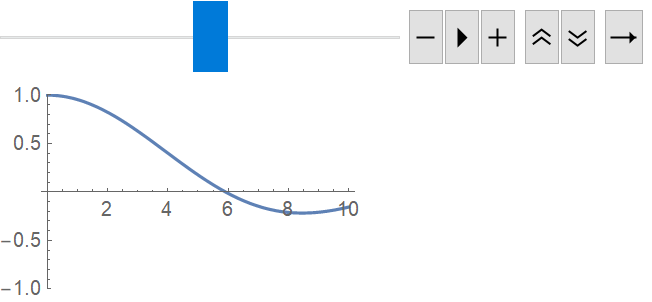 |
Animate a sequence of disks with random sizes:
| In[34]:= |
| Out[34]= |  |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License