Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SimpleCausalGraphCoordinates (2.0.0) current version: 3.0.0 »

Source Notebook

Generate Cartesian-like coordinates for a simple two-dimensional causal graph

Contributed by: Tom Lee, Jon Lederman  |  Tom Lee

ResourceFunction["SimpleCausalGraphCoordinates"][size,type]

returns the coordinate information {point number, time, space} for the causal graph of structural type type (e.g. triangular or grid) generated from the initial node size size.

Details

size represents the initial node size from which the resulting causal graph is built.
type is the type of the resulting causal graph: type 1 indicates a simple triangular graph while type 2 corresponds to a grid-like structure graph.

Examples

Basic Examples (3) 

Coordinates for the simple triangular (type 1) causal graph with initial node size 10:

In[1]:=
ResourceFunction["SimpleCausalGraphCoordinates"][10, 1]
Out[2]=

Coordinates for the hexagon-like (type 2) causal graph with initial node size 10:

In[3]:=
ResourceFunction["SimpleCausalGraphCoordinates"][10, 2]
Out[4]=

Coordinates for the hybrid triangular-hexagon-like (type 3) causal graph with initial node size 10:

In[5]:=
ResourceFunction["SimpleCausalGraphCoordinates"][10, 3]
Out[5]=

Scope (2) 

Create a triangular structured causal graph:

In[6]:=
Graph[ResourceFunction[ "WolframModel"][{{x, y, y}, {y, z}} -> {{x, y}, {y, z, z}}, {{1, 2, 2}, {2, 3}, {3, 4, 4}, {4, 5}, {5, 6, 6}, {6, 7}, {7, 8, 8}, {8, 9}, {9, 10, 10}, {10, 11}, {11, 12, 12}, {12, 13}, {13, 14, 14}, {14, 15}, {15, 16, 16}, {16, 17}, {17, 18, 18}, {18, 19}, {19, 20, 20}, {20, 21}, {21, 21, 1}}, Infinity, "LayeredCausalGraph"], GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 1/2, VertexLabels -> Automatic]
Out[6]=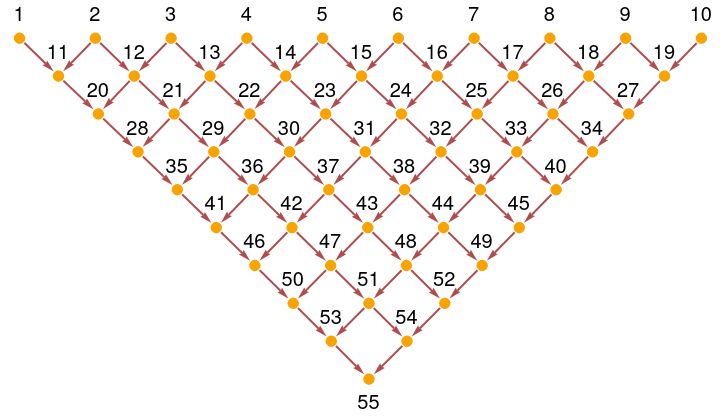

Calculate the coordinates for each node:

In[7]:=
ResourceFunction["SimpleCausalGraphCoordinates"][10, 1]
Out[7]=

Version History

  • 3.0.0 – 11 June 2022
  • 2.0.0 – 14 March 2022
  • 1.0.0 – 04 October 2021

Source Metadata

Related Resources

License Information