Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ShuffleOrder

Source Notebook

Determine how many shuffles restore the list of specified size to its original order

Contributed by: Wolfram Staff

ResourceFunction["ShuffleOrder"][shuffle,n]

gives the shuffle order for a size-n list.

Details and Options

The shuffle order is the number of times a shuffle should be repeated to restore the original sequence of elements in the list.
The shuffle order is also known as the shuffle period.
In ResourceFunction["ShuffleOrder"][shuffle,n], shuffle can be one of the following:
"type"string type, as defined in the resource function Shuffle
ResourceFunction["Shuffle"][…]operator form of ResourceFunction["Shuffle"]
funa pure function that acts on a list

Examples

Basic Examples (2) 

The shuffle order of a perfect out shuffle of a list of the specified size:

In[1]:=
ResourceFunction["ShuffleOrder"]["Out", 52]
Out[1]=

Same as:

In[2]:=
ResourceFunction["ShuffleOrder"][ ResourceFunction["Shuffle"]["Out"], 52]
Out[2]=

Properties and Relations (2) 

ShuffleOrder is determined by the PermutationOrder of a shuffle:

In[3]:=
ResourceFunction["ShuffleOrder"]["Out", 52]
Out[3]=
In[4]:=
PermutationOrder[ResourceFunction["Shuffle"][Range[52], "Out"]]
Out[4]=

Or, alternatively, by the least common multiple of the lengths of its cycles:

In[5]:=
PermutationCycles[ResourceFunction["Shuffle"][Range[52], "Out"]]
Out[5]=
In[6]:=
Length /@ First[%]
Out[6]=
In[7]:=
LCM @@ %
Out[7]=

The shuffle order can also be determined, possibly less efficiently, using its definition:

In[8]:=
ShuffleOrder2[type_String, n_] := Module[{list = Range[n], order = 0}, NestWhile[ResourceFunction["Shuffle"][type], ResourceFunction["Shuffle"][list, type], (order++; # =!= list) &]; order]

For a milk shuffle:

In[9]:=
ResourceFunction["ShuffleOrder"]["Milk", 8]
Out[9]=
In[10]:=
ShuffleOrder2["Milk", 8]
Out[10]=

Neat Examples (1) 

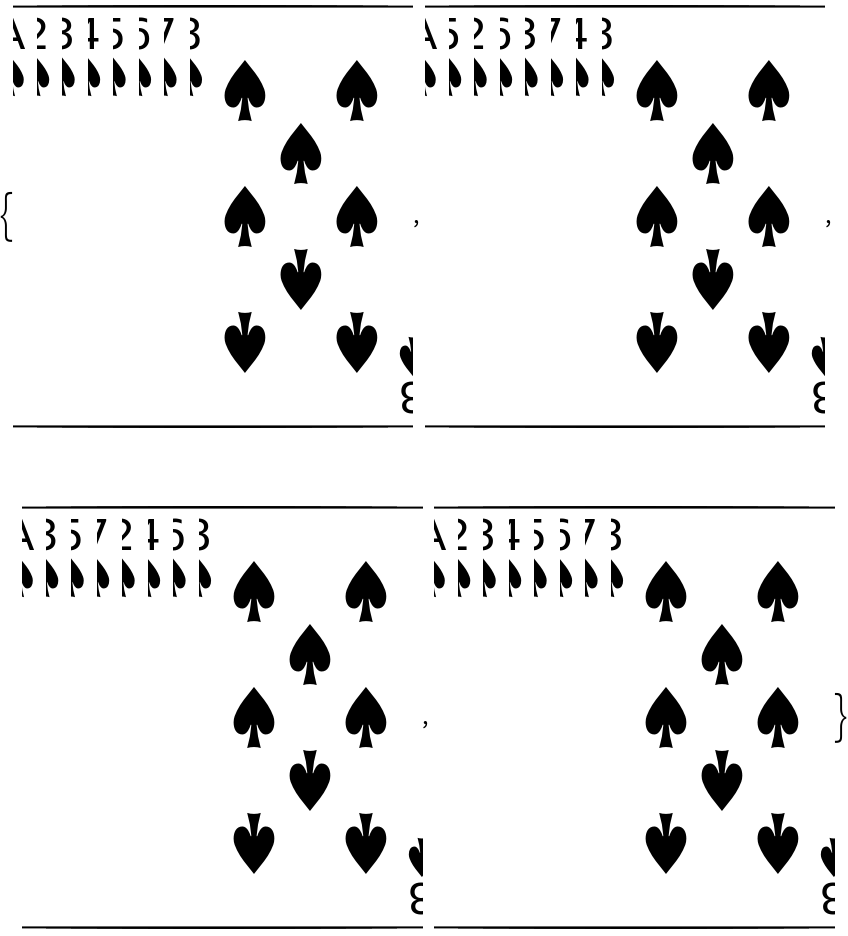
Restore a shuffled deck of cards to its original order:

In[11]:=
deck = Range[8]
Out[11]=
In[12]:=
shuffles = NestList[ResourceFunction["Shuffle"][], deck, ResourceFunction["ShuffleOrder"]["Out", 8]]
Out[12]=
In[13]:=
ResourceFunction["PlayingCardGraphic"][#, "CardSpreadAngle" -> 0, ImageSize -> {200, Automatic}] & /@ shuffles
Out[13]=

Version History

  • 1.0.0 – 14 September 2020

Related Resources

License Information