Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Shuffle

Source Notebook

Rearrange elements of a list

Contributed by: Wolfram Staff (original content for an out shuffle by Sander Huisman and for a Monge shuffle by Katja Della Libera)

ResourceFunction["Shuffle"][list]

returns a perfect shuffle of the elments in list.

ResourceFunction["Shuffle"][list,n]

repeats the shuffle n times.

ResourceFunction["Shuffle"][list,"type"]

performs the shuffle "type".

ResourceFunction["Shuffle"][list,n,"type"]

repeats the "type" shuffle n times.

ResourceFunction["Shuffle"]["Types"]

returns a list of implemented shuffle types.

Details and Options

A shuffle is a permuation of elements in a list.
Shuffle handles lists of arbitrary elements, although the most common application is shuffling a deck of cards.
ResourceFunction["Shuffle"][], ResourceFunction["Shuffle"][n], ResourceFunction["Shuffle"]["type"] and ResourceFunction["Shuffle"][n,"type"] represent operator forms of ResourceFunction["Shuffle"] that can be applied to a list. The specification "type" can be one of:
"Out" perfect out shuffle
"In" perfect in shuffle
"ReverseOut" reverse out shuffle
"ReverseIn" reverse in shuffle
"DownUnder" down under shuffle
"Monge" Monge shuffle
"DownMonge" down Monge shuffle
"Milk" milk shuffle
"RandomSample" random permutation
An out shuffle is defined as follows: (1) split the list in two halves; and (2) interweave each half of the list starting with the first half, such that every other element comes from the same half of the list.
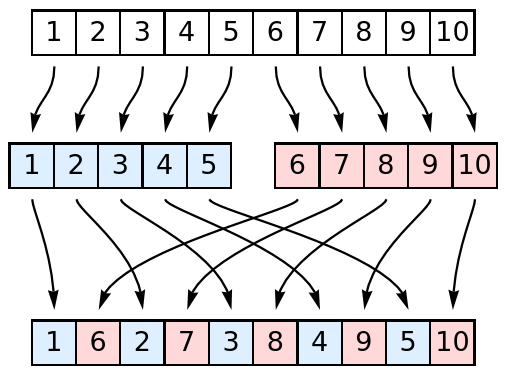
Here is an example of a list with 10 items:
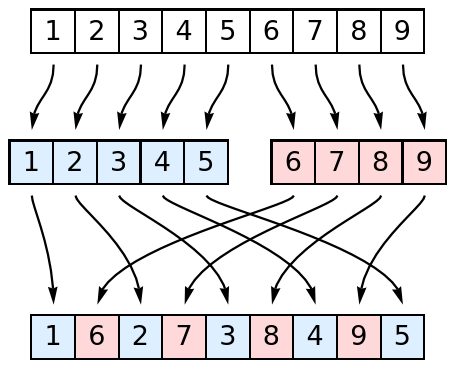
When the list has an odd length n, the first "half" will be (n+1)/2 long and the second "half" will be (n-1)/2 long:
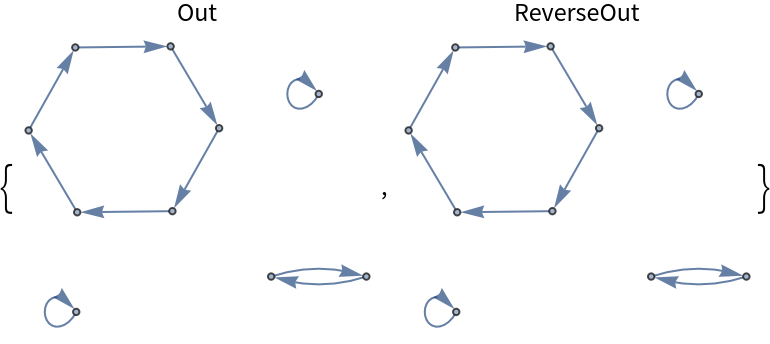
The out shuffle keeps the top card on top and the bottom card on bottom of the deck.
An in shuffle is similar to the out shuffle, only the order of the interleaving halves is reversed so the top card in the original deck ends up in the second position from the top.
Perfect shuffles (in and out) are also known as Faro shuffles, weave shuffles or dovetail shuffles.
Reverse perfect shuffles pick every second card in a separate pile and then join the halves, placing the separate pile on top of (for the reverse in shuffle) or under (for the reverse out shuffle) the remaining cards.
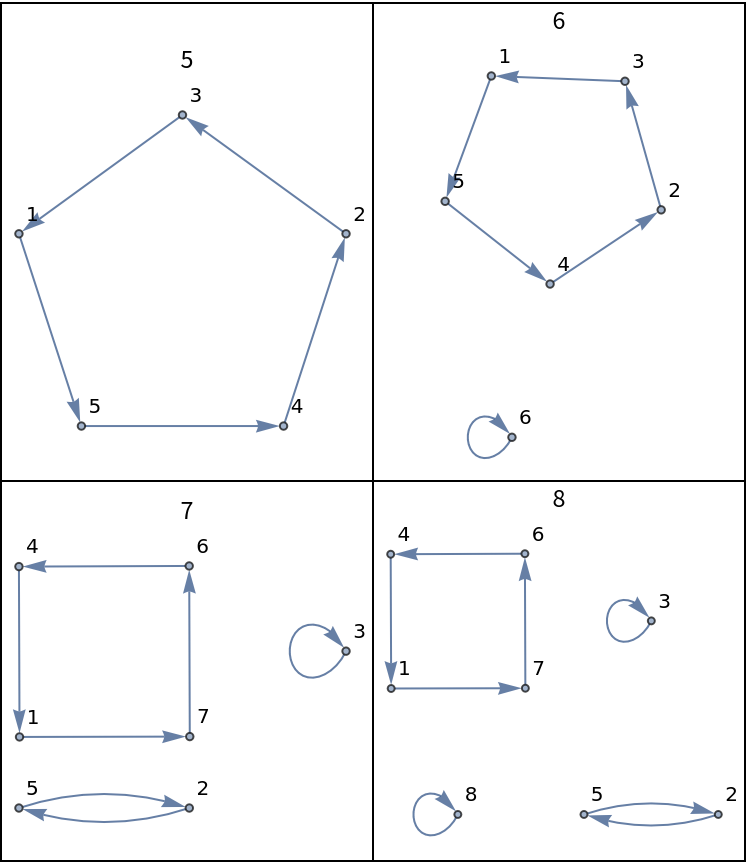
In a down under shuffle, one places the top card down on another pile, then places the second card under the bottom of the remaining deck and repeats the procedure until just one card remains.
The down under shuffle is also called the Australian shuffle, in a reference to Australia.
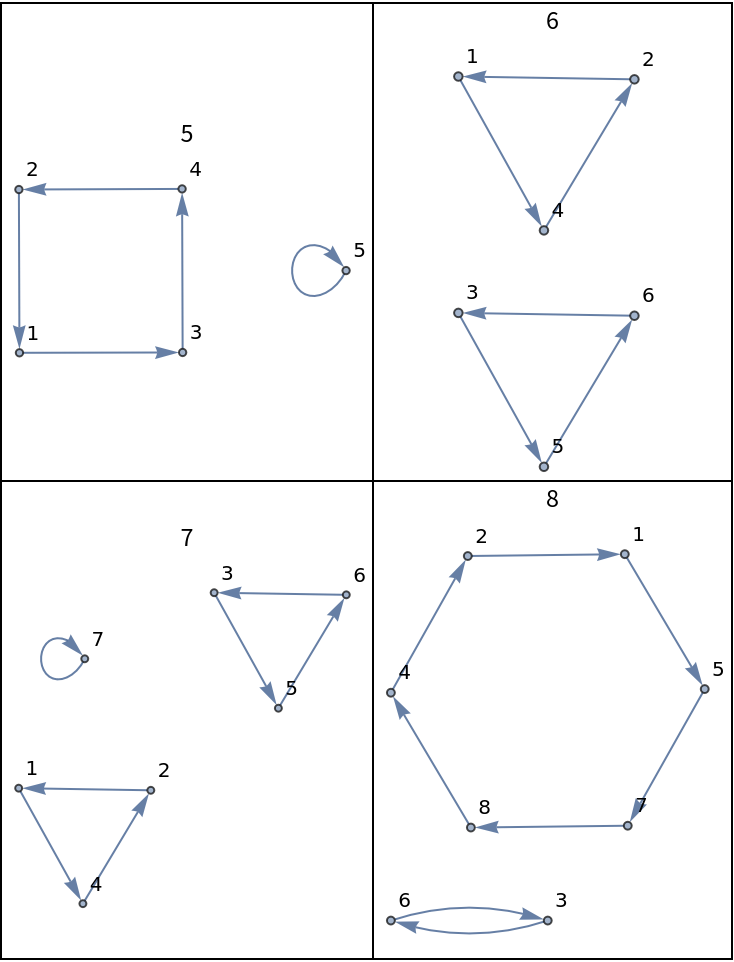
A Monge shuffle is defined as taking the cards from a deck and shuffling them by forming a new deck, alternating between putting the cards from the old deck on the top and bottom of the new deck.
There are two types of Monge shuffles, depending on how the deck is held in the hand—face up or face down— or, equivalently, whether the cards are numbered from top to bottom or from bottom to top.
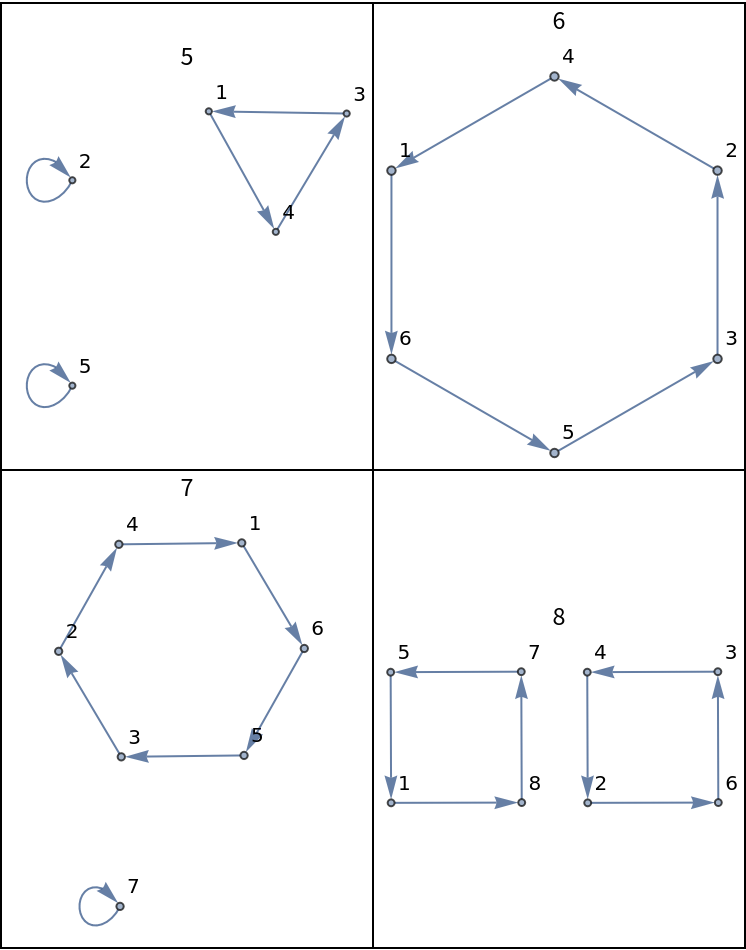
The down Monge shuffle is equivalent to perforing the Monge shuffle and then reversing the deck.
The Monge shuffle is also known as an over Monge shuffle, Mongean shuffle and Monge's shuffle.
In a milk shuffle, the deck of cards is "milked" by taking a card off the top and bottom and putting them aside, then repeating the milking, adding the milked cards on top of the pile aside.
The milk shuffle is also known as the Klondike shuffle.
ResourceFunction["Shuffle"][list] is the same as ResourceFunction["Shuffle"][list,"Out"].
ResourceFunction["Shuffle"][…][list] is equiavalent to ResourceFunction["Shuffle"][list,…].

Examples

Basic Examples (3) 

A perfect shuffle of a list:

In[1]:=
ResourceFunction["Shuffle"][Range[10]]
Out[1]=

Shuffle several times:

In[2]:=
ResourceFunction["Shuffle"][Range[10], 3]
Out[2]=

Use a shuffle operator:

In[3]:=
ResourceFunction["Shuffle"][][Range[10]]
Out[3]=

Scope (14) 

Shuffle an integer list:

In[4]:=
ResourceFunction["Shuffle"][{1, 2, 3}]
Out[4]=

Or a list of arbitrary expressions:

In[5]:=
ResourceFunction["Shuffle"][{1, two, "three"}]
Out[5]=

Shuffle several times:

In[6]:=
ResourceFunction["Shuffle"][{1, 2, 3, 4, 5}, 3]
Out[6]=

Use a specified shuffle type:

In[7]:=
ResourceFunction["Shuffle"][Range[5], "In"]
Out[7]=

Repeat the shuffle several times:

In[8]:=
ResourceFunction["Shuffle"][Range[5], 3, "In"]
Out[8]=

Operator form:

In[9]:=
ResourceFunction["Shuffle"][][Range[5]]
Out[9]=
In[10]:=
ResourceFunction["Shuffle"][3][Range[5]]
Out[10]=
In[11]:=
ResourceFunction["Shuffle"]["In"][Range[5]]
Out[11]=
In[12]:=
ResourceFunction["Shuffle"][3, "In"][Range[5]]
Out[12]=

A list of implemented shuffles:

In[13]:=
ResourceFunction["Shuffle"]["Types"]
Out[13]=

An out shuffle:

In[14]:=
ResourceFunction["Shuffle"][Range[12]]
Out[14]=

Same as:

In[15]:=
ResourceFunction["Shuffle"][Range[12], "Out"]
Out[15]=

An in shuffle:

In[16]:=
ResourceFunction["Shuffle"][Range[12], "In"]
Out[16]=
In[17]:=
ResourceFunction["Shuffle"][Range[12], 3, "In"]
Out[17]=

A reverse out shuffle:

In[18]:=
ResourceFunction["Shuffle"][Range[12], "ReverseOut"]
Out[18]=

A reverse in shuffle:

In[19]:=
ResourceFunction["Shuffle"][Range[12], "ReverseIn"]
Out[19]=

A down under shuffle:

In[20]:=
ResourceFunction["Shuffle"][Range[12], "DownUnder"]
Out[20]=

A Monge shuffle:

In[21]:=
ResourceFunction["Shuffle"][Range[12], "Monge"]
Out[21]=

A down Monge shuffle:

In[22]:=
ResourceFunction["Shuffle"][Range[12], "DownMonge"]
Out[22]=

A milk shuffle:

In[23]:=
ResourceFunction["Shuffle"][Range[12], "Milk"]
Out[23]=

Random samples:

In[24]:=
ResourceFunction["Shuffle"][Range[12], "RandomSample"]
Out[24]=
In[25]:=
ResourceFunction["Shuffle"][Range[12], "RandomSample"]
Out[25]=

Use SeedRandom to fix the order of elements:

In[26]:=
SeedRandom[10]; ResourceFunction["Shuffle"][Range[12], "RandomSample"]
Out[26]=
In[27]:=
SeedRandom[10]; ResourceFunction["Shuffle"][Range[12], "RandomSample"]
Out[27]=

Applications (2) 

Create a deck of cards:

In[28]:=
deck = StringJoin@*Reverse /@ Tuples[{{"\[SpadeSuit]", "\[HeartSuit]", "\[DiamondSuit]", "\[ClubSuit]"}, Join[{"A"}, ToString /@ Range[2, 10], {"J", "Q", "K"}]}]
Out[28]=

Shuffle the deck:

In[29]:=
ResourceFunction["Shuffle"][deck]
Out[29]=

Use a a series of in and out shuffles to move the top card of a deck down into any desired position; for instance, to place the top card under n other cards, express n as a binary number and do an in shuffle for each 1 and an out shuffle for each 0:

In[30]:=
n = 10;
In[31]:=
list = Range[20];
In[32]:=
(list = ResourceFunction["Shuffle"][list, If[# === 1, "In", "Out",]]) & /@ IntegerDigits[n, 2]; list
Out[32]=
In[33]:=
Drop[%, n]
Out[33]=

Properties and Relations (16) 

Permutation cycles (2) 

Permutation cycles of a shuffle:

In[34]:=
shuffle = ResourceFunction["Shuffle"][Range[8]];
In[35]:=
PermutationCycles[shuffle, h]
Out[35]=

Visualize as a graph:

In[36]:=
ResourceFunction["PermutationCyclesGraph"][shuffle, VertexLabels -> "Name"]
Out[36]=

Elements that retain their positions after a shuffle are shown as fixed points on the cycle graph:

In[37]:=
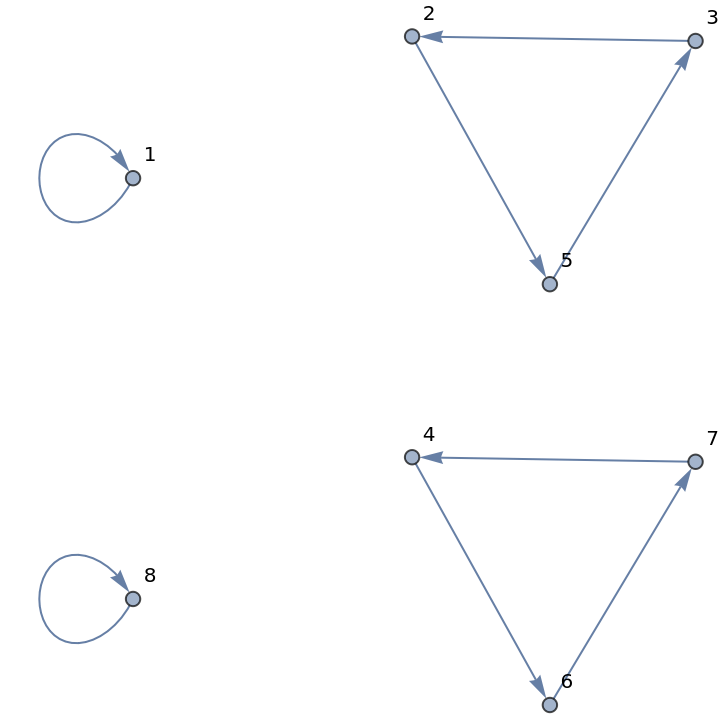
ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[12], "Out"], VertexLabels -> "Name"]
Out[37]=

Fixed points (4) 

An out shuffle does not change the first element:

In[38]:=
ResourceFunction["Shuffle"][{1, 2, 3, 4, 5}, "Out"]
Out[38]=

For an even-sized list, an out shuffle also does not change the last element:

In[39]:=
ResourceFunction["Shuffle"][{1, 2, 3, 4, 5, 6}, "Out"]
Out[39]=
In[40]:=
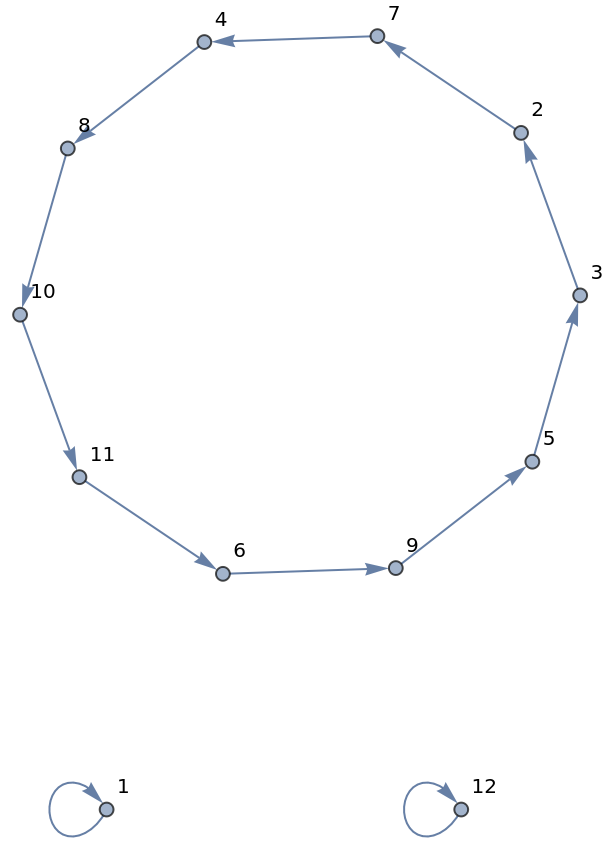
ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[#], "Out"], VertexLabels -> "Name"] & /@ {7, 8}
Out[40]=

An in shuffle does not change the last element of an odd-sized list:

In[41]:=
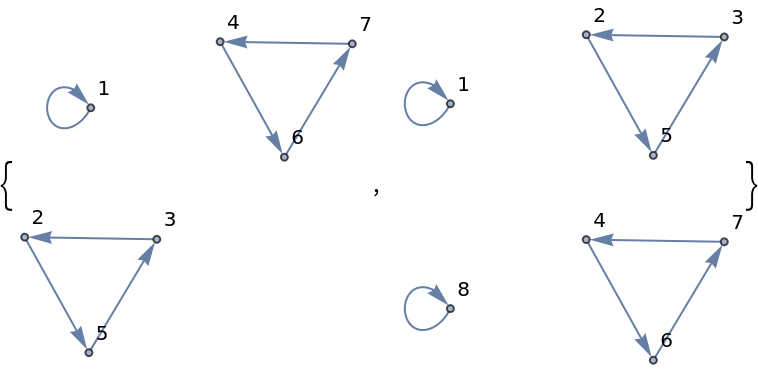
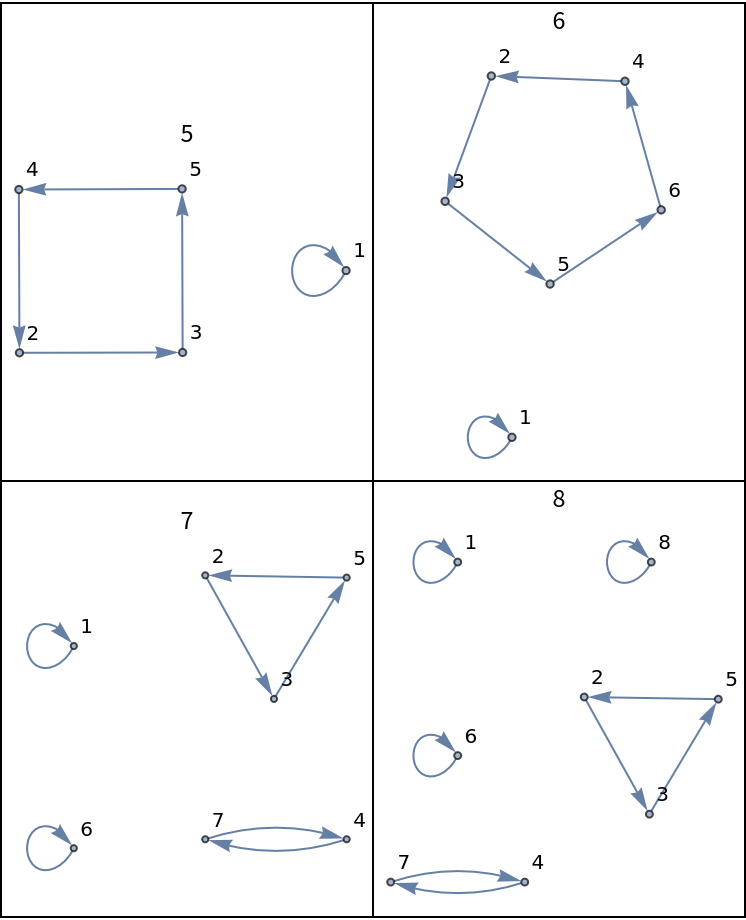
Grid[Partition[ Labeled[ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[#], "In"], VertexLabels -> "Name"], #, Top] & /@ Range[5, 8], 2], Frame -> All]
Out[41]=

Same as a Monge shuffle:

In[42]:=
Grid[Partition[ Labeled[ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[#], "Monge"], VertexLabels -> "Name"], #, Top] & /@ Range[5, 8], 2], Frame -> All]
Out[42]=

A down Monge shuffle preserves the last element of even-sized decks:

In[43]:=
Grid[Partition[ Labeled[ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[#], "DownMonge"], VertexLabels -> "Name"], #, Top] & /@ Range[5, 8], 2], Frame -> All]
Out[43]=

A down under shuffle preserves the first element:

In[44]:=
Grid[Partition[ Labeled[ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[#], "DownUnder"], VertexLabels -> "Name"], #, Top] & /@ Range[5, 8], 2], Frame -> All]
Out[44]=

Shuffle order (4) 

The order, or period, of a shuffle is the number of shuffles that restores the original sequence of cards in the deck:

In[45]:=
ResourceFunction["ShuffleOrder"]["Milk", 8]
Out[46]=
In[47]:=
ResourceFunction["Shuffle"][Range[8], 4, "Milk"]
Out[47]=

Shuffle periods for several shuffle types and deck sizes:

In[48]:=
range = Range[4, 52, 4];
In[49]:=
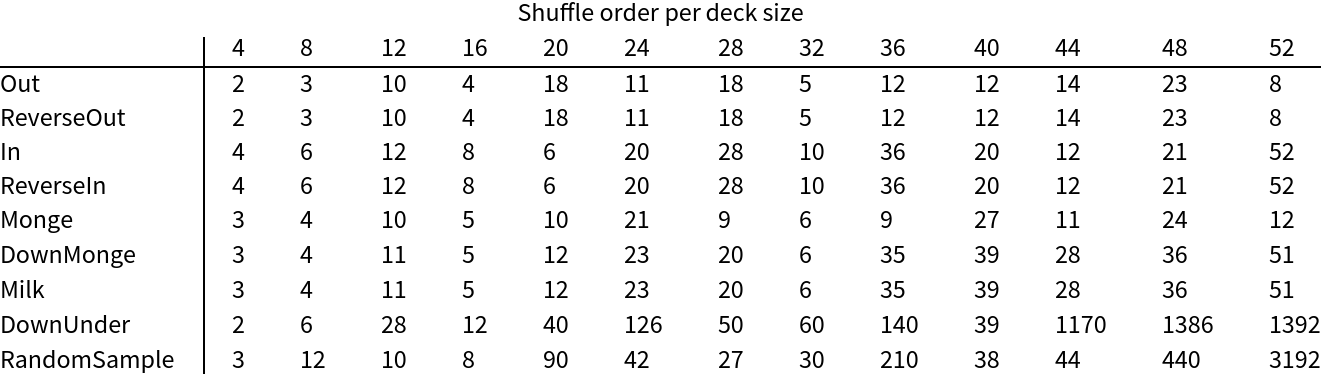
Labeled[TableForm[ Table[ResourceFunction["ShuffleOrder"][ ResourceFunction["Shuffle"][type], #] & /@ range, {type, ResourceFunction["Shuffle"]["Types"]}], TableHeadings -> {ResourceFunction["Shuffle"]["Types"], range}], "Shuffle order per deck size", Top]
Out[49]=

The shuffle order of an out shuffle of 2n cards is the multiplicative order of 2 modulo 2n-1:

In[50]:=
ResourceFunction["ShuffleOrder"][ResourceFunction["Shuffle"]["Out"], 2 #] & /@ Range[26]
Out[50]=
In[51]:=
MultiplicativeOrder[2, 2 # - 1] & /@ Range[26]
Out[51]=
In[52]:=
% === %%
Out[52]=

Shuffle period for a Monge shuffle of an odd-sized deck is the same as the shuffle period of the even-sized deck with one less card:

In[53]:=
ResourceFunction["ShuffleOrder"]["Monge", #] & /@ Range[2, 20]
Out[53]=

Inverses (6) 

Out and reverse out shuffles are inverses of each other—that is, applying one shuffle after another restores the original order of the deck:

In[54]:=
ResourceFunction["Shuffle"][Range[10], "Out"]
Out[54]=
In[55]:=
ResourceFunction["Shuffle"][%, "ReverseOut"]
Out[55]=

And vice versa:

In[56]:=
ResourceFunction["Shuffle"][Range[10], "ReverseOut"]
Out[56]=
In[57]:=
ResourceFunction["Shuffle"][%, "Out"]
Out[57]=

Shuffles that are mutual inverses have the same cycle structure and, therefore, the same fixed points and the same shuffle period:

In[58]:=
Labeled[ResourceFunction["PermutationCyclesGraph"][ ResourceFunction["Shuffle"][Range[10], #]], #, Top] & /@ {"Out", "ReverseOut"}
Out[58]=
In[59]:=
ResourceFunction["ShuffleOrder"][#, 10] & /@ {"Out", "ReverseOut"}
Out[59]=

If k is the shuffle period for a length-n list , then the sequence of elements after m shuffles is the same as k-m reverse shuffles:

In[60]:=
n = 52;
In[61]:=
k = ResourceFunction["ShuffleOrder"]["Out", n]
Out[61]=
In[62]:=
m = 3;
In[63]:=
ResourceFunction["Shuffle"][Range[n], m, "Out"]
Out[63]=
In[64]:=
ResourceFunction["Shuffle"][Range[n], k - m, "ReverseOut"]
Out[64]=
In[65]:=
% === %%
Out[65]=

In and reverse in shuffles are mutual inverses:

In[66]:=
ResourceFunction["Shuffle"]["ReverseIn"]@ ResourceFunction["Shuffle"][Range[10], "In"]
Out[66]=
In[67]:=
ResourceFunction["Shuffle"]["In"]@ ResourceFunction["Shuffle"][Range[10], "ReverseIn"]
Out[67]=

For an even-sized deck, a milk shuffle and a down Monge shuffle are mutual inverses:

In[68]:=
ResourceFunction["Shuffle"]["DownMonge"]@ ResourceFunction["Shuffle"][Range[10], "Milk"]
Out[68]=
In[69]:=
ResourceFunction["Shuffle"]["Milk"]@ ResourceFunction["Shuffle"][Range[10], "DownMonge"]
Out[69]=

For an odd-sized deck, a milk shuffle and a Monge shuffle are mutual inverses:

In[70]:=
ResourceFunction["Shuffle"]["Monge"]@ ResourceFunction["Shuffle"][Range[11], "Milk"]
Out[70]=
In[71]:=
ResourceFunction["Shuffle"]["Milk"]@ ResourceFunction["Shuffle"][Range[11], "Monge"]
Out[71]=

Neat Examples (4) 

Shuffle a deck of cards:

In[72]:=
deck = Range[8] // Reverse
Out[72]=
In[73]:=
ResourceFunction["PlayingCardGraphic"][deck]
Out[73]=
In[74]:=
ResourceFunction["PlayingCardGraphic"][ ResourceFunction["Shuffle"][deck, "Milk"]]
Out[74]=

The shuffle periods vs. deck size for an out shuffle:

In[75]:=
ListPlot[Table[{i, ResourceFunction["ShuffleOrder"]["Out", i]}, {i, 300}], Frame -> True, FrameLabel -> {"Deck size", "Shuffles period"}, PlotRange -> All]
Out[75]=

Recurring patterns in Monge shuffles of different-length lists:

In[76]:=
Table[Labeled[ ArrayPlot[ Table[ResourceFunction["Shuffle"][Range[n], x, "Monge"]/n, {x, 0, 20}]], n, Top], {n, 10, 20}]
Out[76]=

Card movement after repeating a Monge shuffle:

In[77]:=
Table[ListPlot[ Callout /@ ResourceFunction["Shuffle"][Range[10], n, "Monge"], PlotLabel -> ToString[n] <> "-shuffle"], {n, 1, 6}]
Out[77]=

Resource History

  • Date Created: 14 September 2020

Related Resources

License Information