Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SerflingFit

Source Notebook

Fit a Serfling regression model to a dataset

Contributed by: Naman Taggar

ResourceFunction["SerflingFit"][data,d,omegas]

fits a Serfling regression model to given data with polynomial of degree d and cyclic terms corresponding to omegas.

Details

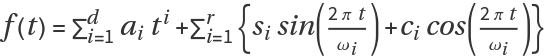
The model was first introduced by Robert E. Serfling in 1963[1] to track baseline influenza-related infection by analysing the seasonal patterns of disease spread. The model takes the following general form: where the first component is a polynomial function of degree d and the second component consists of r pairs of sine-cosine functions to resemble seasonal patterns. Originally, Serfling introduced it with d=r=1 however additional sine-cosine pairs can be added to reflect specific periodic patterns.
The coefficients ai, si and ci are the regression coefficients whereas the ωi are the periods of seasonal patterns. For example, if infection occurs twice each year, then a single pair of sine-cosine functions with ω1=26 (in weeks, assuming data is weekly) can suffice. However, if infection tends to peak more sharply in one season as compared to the other, adding an additional pair of sine and cosine functions with ω2=52 (say) can help reflect this annual pattern more accurately.
The data should be a list of target values yi or a list of (ti,yi) tuples. A list of omegas should correspond to the pairs of sine-cosine functions needed in the model described above.
Ordinarily, d=1 (linear polynomial) suffices, however additional polynomial terms can be added such as a2t2 to model population growth, if needed.

Examples

Basic Examples

Create random data with seasonality:

In[1]:=
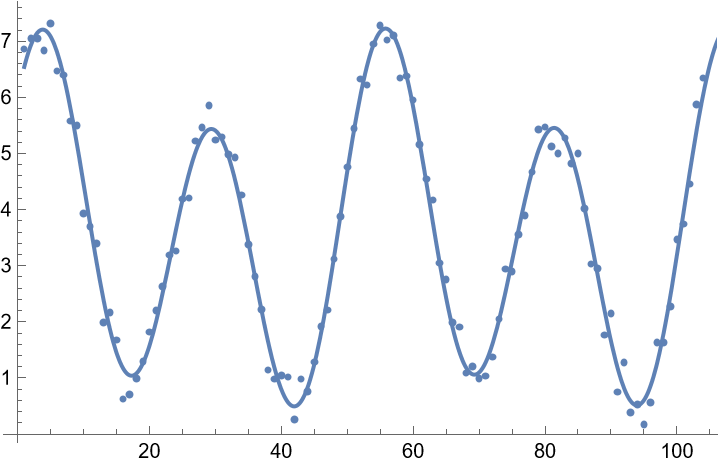
data = Table[{t, 2 + 0.025 t + 2 Cos[(2 Pi t)/26] + Sin[(2 Pi t)/26] + RandomReal[{-0.5, 0.5}]}, {t, 104}]; ListPlot[data]
Out[2]=

Fit a model consisting of linear term and 1 pair of sine and cosine functions with cyclicity 26:

In[3]:=
fit = ResourceFunction["SerflingFit"][data, 1, {26}]
Out[3]=

Compare:

In[4]:=
Show[ ListPlot[data], Plot[fit[t], {t, 1, 120}] ]
Out[4]=

A degree two example:

In[5]:=
data = Table[{t, 3.5 + 0.001 t + 1.8 Cos[(2 Pi t)/26] + 2.1 Sin[(2 Pi t)/26] + 0.7 Cos[(2 Pi t)/52] + 0.6 Sin[(2 Pi t)/52] + RandomReal[{-0.5, 0.5}]}, {t, 104}];
In[6]:=
fit = ResourceFunction["SerflingFit"][data, 1, {26, 52}]
Out[6]=
In[7]:=
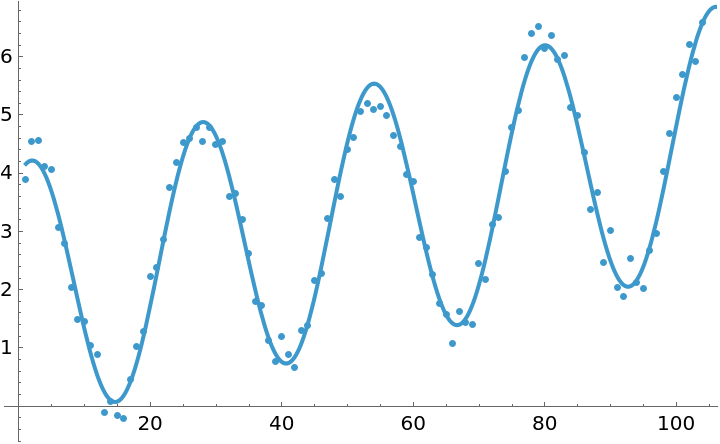
Show[ ListPlot[data], Plot[fit[t], {t, 1, 120}] ]
Out[7]=

Publisher

Naman Taggar

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 27 June 2025

Source Metadata

  • Citation:
    • [1] Robert E. Serfling. "Methods for Current Statistical Analysis of Excess Pneumonia-Influenza Deaths." Public Health Reports (1896-1970), vol. 78, no. 6, 1963, pp. 494–506. JSTOR, https://doi.org/10.2307/4591848.

Related Resources

License Information