Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the sample entropy of a time series
ResourceFunction["SampleEntropy"][timeseries,emdim,rfilt] computes the sample entropy of the timeseries with embedding dimension emdim and filtering factor rfilt. |
Show the sample entropy of a time series from a uniform distribution of real numbers:
| In[1]:= | ![SeedRandom[42];
rndmts = RandomReal[1, 1000];
ResourceFunction["SampleEntropy"][rndmts, 2, 0.2*StandardDeviation[rndmts]]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/6b634515a309a58b.png) |
| Out[3]= |
Set up a nonlinear time series in the periodic regime for the logistic map:
| In[4]:= | ![lmaptsper = Drop[N@RecurrenceTable[{x[t + 1] == 3.5*x[t] (1 - x[t]), x[0] == 0.1`2800}, x[t], {t, 4501}], 501];](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/3081a5d57db0dd89.png) |
Show it:
| In[5]:= | ![ListLinePlot[Take[lmaptsper, 100], Mesh -> All, MeshStyle -> AbsolutePointSize[3], PlotStyle -> {Darker[Blue, 0.17], AbsoluteThickness[1]}, PlotRange -> {Full, {0, 1}}, PlotLabel -> "Periodic regime \[Lambda] = 3.5"]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/47b14cb8a796c6f5.png) |
| Out[5]= | 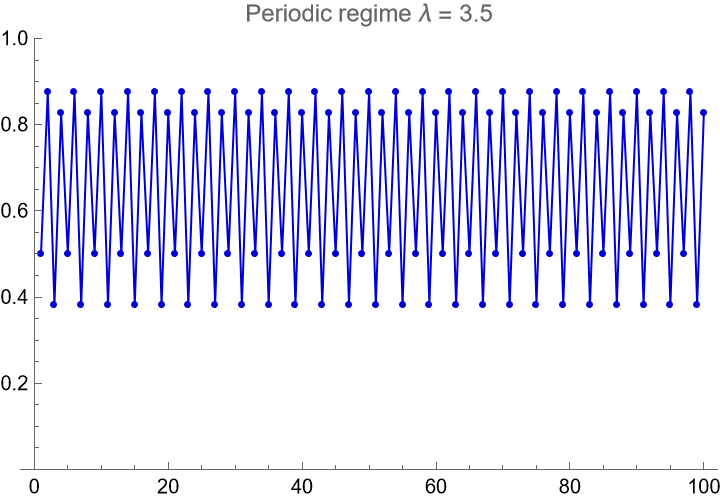 |
Verify the SampleEntropy of the periodic time series is zero:
| In[6]:= | ![m = 2;
r = 0.2*StandardDeviation[lmaptsper];
ResourceFunction["SampleEntropy"][lmaptsper, m, r]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/468d4121493b7255.png) |
| Out[8]= |
Change the λ parameter in the logistic map model to set up a chaotic time series:
| In[9]:= |
Show it:
| In[10]:= | ![ListLinePlot[Take[lmaptschaos, 100], Mesh -> All, MeshStyle -> AbsolutePointSize[3], PlotStyle -> {Darker[Red, 0.13], AbsoluteThickness[1]}, PlotRange -> {Full, {0, 1}}, PlotLabel -> "Chaotic regime \[Lambda] = 4 "]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/13ad89e3d9c782ef.png) |
| Out[10]= | 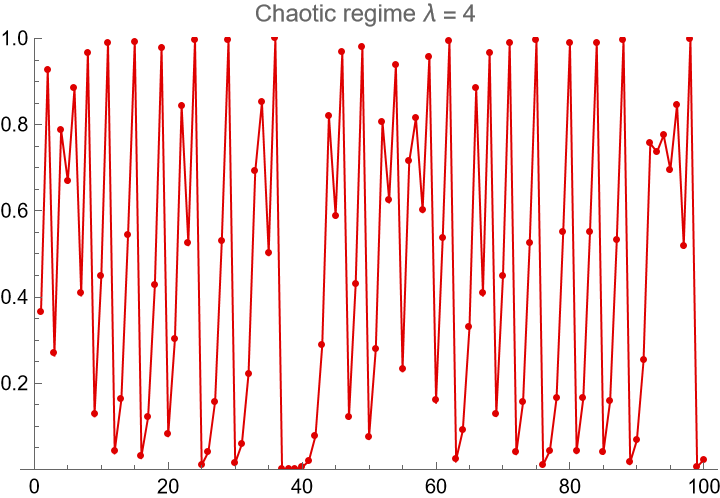 |
Verify the SampleEntropy of the nonlinear chaotic time series is nonzero:
| In[11]:= |
| In[12]:= |
| Out[12]= |
Show the sample entropy of a time series from a uniform distribution of real numbers with the delay set to τ = 2:
| In[13]:= | ![SeedRandom[42];
rndmts = RandomReal[1, 1000]; ResourceFunction[
"SampleEntropy"][rndmts, 2, 0.2*StandardDeviation[rndmts], 2]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/6434738147826975.png) |
| Out[14]= |
Show the sample entropy results computed for two ECG signals taken from Wolfram Documentation:
| In[15]:= | ![ecg1 = TemporalData[
TimeSeries, {CompressedData[
"\n1:eJwl1wk0VO//B3BJZSkktEklZWklW8igDdkSUSlkS6JsWVKypFBkKYpKWrRQ\nlCVL3pLs+26Yca9dqaQIlf7P9/d3jvM5M889M3Of87qf5/1Ze+KMiT0nBwfH\nHPI/MpeD487t//46ERrw/7VR+P9rk3nC/+qdZ9f/V4/u1Uj4r1YJCN38rw7O\n47nxX21IfXfxf9cPG274rz4PWncgntSnydkpN0j9+snr5zlSpZ/lKYiQ6qpX\ne744vhM83FYvw2M7kXl0mPvclU4E209yap/sRHLf8f6u1Z3YkRa83j6sA16c\nB60V3duxw0rcuP9xK75ZcunYczdjm6eWb8GZelgd4RTV21eBjLTwrWVzSyC8\nMVM/x6kQTw/YMaL7C8BZ7WKmbP0epS8enLS/Ww5jMZ7v99bXo/b8/HWGys0o\n4VNf4qrcBuWp3X/kr3ZgQmpnp8uKLohHRpjWMXugerbkPZ3bizt6C1+zt9NY\nMeY+7c1Vjo4nFUGB7C7G6nCH3puZwwwN+faOaotOhmi9WzdTuREdgt8PntIf\nQMKIs6+szSAsxNMtfy7vBVNDZ0D/HQtua2c0tY90YZ737Z3KRkwwbbRKguU7\nMYdL5L5MZjsO34gXm85qRWLrySE5pWb0po/vF1NvwKqqJHPXkkpczbH6xPO8\nBNf4eZlpjrng0AkNKP7xGJqNgiECuZ6gEku37tkZw+DYY7folF8845KG74Ji\n3WCGoG+kmv+/m2gZVQi/IJAJffesnwVrgDdP+niPK5RjzV1Po/KWOkyJ86z4\nOdkE/0ranFOoDRzv5cs8H3YgVHe6Ke8JE2rjBi//ru+Gn+dLKW8FFnS/K44s\nH2FBfHNEf9ARNkbuXGs9lcTGmhmbj4FFbCyK5aWO17BRIZH/kLOOjacTiv3J\nFWyoa7ttOA02mDGZokav2dDWvOF48DEbgu91x3wS2MjKnJBEBBvh9f456wPY\n+GQ7FJrmzoan+54vJg5sBCRvrF9Gvi/p2YWlswZsSGyPK+LQZmOFgaidmBIb\nl53enNkly4bS9ru62uJs6Bik7D+9mA39VO739XPYYH/ObTv7iQVVh0fB/MUs\ncAScvZ5wmoVLAkFzt1Z349aTOH2pZ134OvExd3lTJ8z2h76ZkWmHSdL9itG6\nZlwa9DLW3daAYOeHvM7cVWjjzLFcsr4MTKcnLap1H3GaTnXbLl2JyM1i768d\nqMfeO1w7BW2bYW6p9Lvzbxt21p7ytf7ZCbaZw9VEtW4w6L2O9qXkvn87NeS9\no9GQP3H+VnA/mIvr4+b87kWhu6HBIH8dDuldeKV5ooNhmyW+i/41yHh7oZ+p\n9rWVIao3lf7ydguMh69s55sehPh2zW+hPMO4zpfTL1rUhzSLHP/EixSi+iqS\neqPZeJSZ9e/xRRZsGmpXtB7uhkWI7kX3BiYWRmskGtZ0wNwgJfjpnjZYO4sv\nLN3VjAVBm6dNSuqxe2vKwNM7FeC/x3PU5OZ7UM8WLaXv5eBGi1GY7+Nn4JjU\nihc4lYg1SgHDK/NuYuqznRTr+gNY+io5BMVmQCF7beLg/EJMH1gmuHy2FD4x\nayx042pgORYydmlJE8q62JG7brdiwxGXuKT0DlR8TlriptKF1gnTO5KKLKzy\n5Tzdl87Gyp1VrJHsHugfdjkrIk+hbF9ybLIjhW0BFsHulylUyxS8toulYOqe\nuVQ7nsKJI+/qeW9SyHUaTrOIohAXHzdceoWCh91hxd1kX671ReR1eVJYvVlF\nP8KZgsip8iCTExQKKlz2yR2m0KPisVvKmMJ0we3dCvso6ITQnBYaFHyWBnyN\nVqRgVWj4md5EYeexkdQ9khRm/ym4Za+kIB07NSW6hMIa9x9dwrwUJJmurq7/\nerDPNPPubG8PDIpkPyS86cGfcW9d2aPktfWHruYsNnwleCc/X2dh4EFB4PzX\nXbiXt+7+6nmdkLnQvOow6Yctlgx5Hs4mrLt2eMuzlFqYjHJvlsypxPSzV0Uq\nhyoRLTQzKZ1ag5nw/H91to2oPGq1683yVhioi68Wz+iAUubL4MMpXZBIHys2\nGWBBNO7al28KFDrM9qw9FtmLNIdnkjImA1iz9GdLSHkfxO3zhxyTGnDxqCHP\ngcY2houOo62T3CCjZb6N9U77FobkITqoQrwNiQ/MEp7kDWFKLcNbuWIYW8Ii\nmbRfP5Kfafhd3kHD9Y3A39k5FJLtfnQLfWEj7qvLlaRSFvjOqTXeVe5G7Oxt\nvqGtTHzf3yyV+7gdxqdKBg8kt2DMptmGodqIese3PL/2VKNxQ2Bp845SCPsa\nzXNhFmBTz97tkxyvUbxfNm3xr1RMOVdM+3KRvniqlD2W+AL63bN6edez0W3l\nulrFrxj3vLiD413LEZWi1Hljtg7SavXno/c04+Nb61Cdijb0ef+KvtvZCdX7\ned1eNt1I3nE9V+EoG+lVhn7zG3tgu1nt+RLiZIHYL4GPxRTCWXYF/T8pbLKa\najRcTJ7fqPNF3ato1IWVuBxeQ8NH3fdHqRi5f7p/aZ4IDc4bEXz1C2lEbNJ1\n+z2HRkXxebddvyhkhpxsezJKvHH/27i+l4KZsdjRonYKexzZE261FNrqPnYw\nPlB4yyUTLZVHrnv6uVb6FYUWczPRXY8p8K/jFfNMpFDaMPd0VjSFKq/Uuk/E\nOa+2skfxBQovR33y1d0prFQanU8T3y1q6rkL9SgcUPv2LUeMAjefydPeGz0I\nf3o3uNqRDb1T0quLw7oh9PuzTjazEw4MjtganzZ8D3FWtm5uQsQf/yoZLXIe\ncx37HGJcjZUrRk8FjlYhwaHJ7uyOOnwNEHgxJtsEFdWk9jZ2KzbZbNxg4NGJ\nuKgnMjdsu8EdFTsQ/4iNQKvcxffJ8/qB38xAbLQXjxI8Xk2+HMCjuQFSjuv6\n0aSSssvCpBGiA9ts5Ve1MX7v2rtRo2OAoX9uG8+rrGaGeOOk1Y3aNuiNxfFv\nERzGoy126fSqERjnP32dXd+PHbtHOAKu07DsvvpZwozCkb2Ln72O7oH/F78F\nt8l9Wr/Slfnd0Y0m8B9/Vs+EqvTD8N5dHWCOh579pN4K/2afTzqtjbBfssP/\np08NHB7+k/zg9BGWW/drMxSKwB1SnFVtmgXNDfyFVEwaMrrDRiPinqHUuV9U\nXjADWbGf3spV5cLyyXuNRNI3JxRNGqSvVGDvj+qijbwN8BWynLOkvhnufdof\nnY3bYWQhKOJgzcSVZe+Fhga7kSHz9ceBHjY0NHPjR2QozFE0cW1+QYHPzXug\nh4PG1ErvPZYKNApL+DIljWmI8ExHClnSuPc4u3zsGA0P7eBTOEyjWshDbZkJ\njZojYw5xOjTm/bQPl95Jg57uru2Uo5EhFTKRuoFG/xPe8JiVNBaej3G7LUjD\nIr1XqXAeDVnjN3kzM6TfTZr6mo5R8Ppsu6NygPg0Tzey6CL9Ucgw8l8DhfJa\n6bDcMgpiIiPZ9oUU6qPnCWZlUqDGYfOCOP1ga5FYQ/rxp4kz2t7+FNK9Ft58\nYEhhiQzL8e2PHiiEzJN9XEnO84P/spI/daMuu134nioT9IGaoPftbahcuE3I\nVq4Z0bfGrh38XY8418aeJu4aBD/Wyud6WA0ug3YX0a912HJkdaFVSBOCdNSm\nbUneiwxvr5iu6sSh2W8nLfO78Uq6ec7VGTYGNAo1ZIso3LYP5VIX7cPU49Ht\nzzsGcMXVOz1dvx+upmeTlzxqxFN2sPXumlZG+1zNs1syBhjif9ztDts3M5Tt\nji6WFGuHWKKTkYDyMITuTrRb7x7BDU2nlQ0T/RBe/tZG7Q2NBfSOWwF+FDji\nl6Skd/XA1MDhQXsGGwuPee4IWMuCobXnS8+lXeD0Mv07Gd6BOFvOVt3gVgzd\nfB4wsaIJPxbI645w1uJXfo/q4fGP+KNqI5itDdQM3bsSbp0N68lbT5Y8fgmV\nazctLz14Ac/7m2KEhDNhzard6FP9Fh3zQyanhEvgPhNesHteJXR/xWvd0WmA\nhdjAXPbCFpSUOZonXm/HZZ00/E4iee9Y8ntKgoVgOWH+jBU9KDb0FDUg598/\ng1GD0QoKP65X9b4kfS5n+50FvcRdp5znrM1pGg9XzQvl9qFRtbZk6L4vjenb\noTulvWiUqE1qq7nQ2Hi/XtndlrjrZQ6/N6ehumap81Z9GiccGy/ka9KQ7zv7\n9IQijQez/vVSsjSKvAXO86ymcS5UP2KBMI38qUa/tTzEaVyvsPksBcH8goTU\nHxRWyPB9Ehyh8DttV2IEm0JAQK/A32Zy/i6ee1CgkkJ8oJVMNfF48Ox3/8w0\nCou0+RrXkr7zqjP4pJA9BZVWre4lghSWV/PoPZwgOWnapGyLKAshMx+3vrNn\nYus33nZ3znY4XxdOTj3aDPbV80lBUg2Y/hiT9upoDbydNi4SmKjGe5XH+kaM\nepgcuhUel9YEi4srUuSt2uB6XXfwxHgnEoRKv1vR3VDP8xuSXtuDxQkPzuk2\nknxWwBDaKNOH+rBNISc/D8Ay2KlX3aofSv1BUfUVjVgTweH/ObWVYb9rZbD8\nvQFGzFXh6EKtZoZ6ygvagdGOnzEOVcE6w1Bx6vd/ajaC0wd9kj7NH0BVv0WQ\nbCkNR7lJee0ICjMlxuK9f3oQ0iBrmtvIRrfv2xEebRbeOWS9fqHcBS6HvsfM\n5x148vDjTlZKK5hrwnYrqTaB67LeSLlmLa79Ur95c2sZGna3p30uADJmZ+iI\njmxYJHS2Nse8wkn38oiX19KgEJG3JPJqJqYc/GX6NPJQ1+iiuNywBKbMuZfa\ndlbi1vywxgS7BhS+XJ8UL90CFbvtdYuetaOO/3i35FsmllwsSyG/AGqfnvwz\nVuwhz5/mPX9TCkFt7otmWimYz3ecuEN8xFp3KqWTPlcXXP9rIfGmcYQ/NSaE\n9DntA9K8oTTW/ta47BFIQ91nvZgjWS+WeFxz8Qw5p2PGal8Rh8YnV32ZJQ4l\nYxZ+ciYOAwTu7J8kDmNcgifuEofX9GtdT5Dv2VadGL+LOEzflj+sSRyOR0du\nO0IclnErP4okDuWr0rd2E4ciT6ds1YhDx6zgu9HE4ea8jC9XiUO/1+9EZcsp\nTKYs4pjMoaAk0b9R/y4Fp6/LeiTOEL+vd7/iXUHh1IVrm47z9CD0hoFjrgwL\nG3W/LhT2ZSLFT9EnQaQdBhk9PkmuzWgZNNmwT7UBm3Ll9nReqkG4dqUyc3kN\nWr5zRRXa1iP8h0RWUlETrNf8mF7o1oZ9FdfvC3AxYcPZaMYa78b6segmb/ke\nXNrqktrdSWHQrqb/iVwfZiXDIup+DODqpsOrIx37sWBxOluvsxE5PPeGY+Jb\nGevNThsJ3xpgXEzPjM6Va2YoTs5r0jJqh11MoY+l8TAGo9bccDk2glfVUqa3\n+QcgtdHQvrKaxl6/KrophuSPBwGzn+ZR+BXt0x9KkXmw5a1kljELU+/X5W3b\n24XZr6sWq+V1wEf5cNOKzFawK36vMNRpQnEIOz3bshZDXCKbNfeXoWXgA5U3\nDugIO59q5c+B9EBdivzsK+is/BGw5lca9GUqIze/I/MuZfjut3seTh3cHtTl\nWILlDQo9ZuaV2OJ/Z0zFrQEF/UI/RBRb0LXBtdI1ux2RFkX3bEuZ2GOTKjik\ny8L4ofzPZlo9eHg+yvnMETJPlKv+YJHzzokVq3V2G42EfzsDPIgjDQMz6sNF\nGh8zHETUwomzsuNpDyNoDLssov8ShytvbNHqI+v6cnKTo57EVfo6CUEn8rrL\nPeoA8fvy8aG/GQdo+Me7jG/eS8N9/lKTClUaXy5RKQFbaSg96i89KEk+L1l2\n2+7l5Lw38Mgy5qcROWkU5DOXhsyrq2F5UyT/+R45svArBS5NZcNDfSRXPt/q\nq9VB4fUW26S2avJ+j8i9WwWkL24T5KAfUPC+zs2d5kHhb8J6vaviJM9uvRSo\nLdQDzRQu0cvyLCS9WmxYHchEne/g1R3i7bgueuy6lHcz9ohYehVqN0Dg1Gtm\nQnQNknQr1M/I1mD11S5tKc96qAe6rHpX1oTjfIcKl/m24VKLef38hUwMjGYL\nFM90Q1k+qm6vag/WKaduymdRyOBpOu+n2IdlP7TOJvwagOyBRccMnfshW5Cw\n8y3ViFKplR4qN1oZb/wSg8/GDDA4Y85YB8k2My4+y75md6gdR8wjjPsODuN7\neqjMV+sRTBV9C1wiNIBNm+yPKtbTaDZvvy1/i8LDBKff2jwUYpyv75IcYqMl\nQOq2ljkLiqd3PX6p3wX7C2Giz9CB2ScXjH1ySf57E1Rz27AJkjIFhfJOtVA2\n94tKMi+DrGT6iaR5xYg7pTM2XyoHml8alGWXZmDb25U7gzekI25MuyCjJRPL\nXj8o0gzPw9kNgZFWHiWoVjmzqeBEJbg1I9hd5xoQ/fKfabpqCz5tCvoznd8O\nJdPlXgOVTBQnX3l20IgF4+1nvmft7UFw3G/m0mMUDit5GgeQvrJ1sdwP3u00\nLh1jFi5wIP7Wu3w+QPrcpy960yXXaGzVuvBgfSRxdOlojm8YDU+VhxMWZD3r\nSMs5S2/SN2+8Pu3rTOMVf1J2lhWNo4dz+flNyecZhs2GkHzoJbrn5HKSD/9d\n3t1URfKhom+S2G2SD1Mm/hQFk3z49kdZWDjJh1sL3F6kkXxoI3JNZJjkQ9va\nMXNFkg/PswqqfEk+DMlXCrZikvlb4K/WNzLHcJg1jj57R2ELds379pCCTIlb\nY5YXhauhnf0RayhcOrfMkyFK8tFDIcpbiQX5nhnurMtM7NCTMF4m0Y7E34Y+\nf/yaEbo6MunKXtL/glW6V96ugf5fJakeuRoYFXrLh5yvx8uAr9tOVDVBpDbn\nWpZ/G1qKi+1uCzDxdcEcX93ZboTlBR4r39mDu1u4fnv1kPmtKa9VTrkPKx1G\nzu6fHsDp2dM8f0/3o6hdmWtRfyP8Nq6WHr3WysgLHImvuzHAuDd9uWavVDPD\n60MbM/5wO65yeA36mA3jaaJXbsCJEcR05PM8WDKAlzV/JosaaPDrKO9/G0/h\n0Mqo6lJeCmVL45TWfGJjw5nGccUjLISKlfskGnVhX9Tzc5ElHTh+zcTkUD7J\nf0v7L5490ARWEf200bUWng/SNm0+VoakBpEWcb5ibHPTy/8ml4Op7zM7fq3N\ngGBxnMGgWjoapLdM7+3JhMX9OYsK4/IQErunK8qnBIlWbG22YyWm47JYDr4N\nEFa50im3swXJl4VW+LxrR5jiMcVjNUwoD4pIfDzAwkXZAbk1uj24NtRnr3ec\nzJmMlLqXZL+c9nGdViZzR2OYjIqcI4279WvcfIJoSFxWjB4k85bCWJ3J3iga\na1Q1rsaTfniU0/ybB1n3iYi/70ny4QO/yupIkhelH8mYlFuT93/i2yozGt27\n5m2M0aVBySwfWqdB446RxvMmeeLtXKjpPSka33POHwsl83Qr9eFmOJm3PcdH\nZJ/PJ9eX7xbo+03m3b+BTZu/U3hzVqbmzCCF3mI+oYOkX4t6h9tRdRQ0zbc+\nSyB5nxnqZtP1iMwhHXea750jffF9T4zHWgqRvU3beZf14PVZHQENFRbq+0Tf\neF1hwj3IK7B1XTt6FWzVsv2bcUr09B81kp89ut59O59UA6snN58oKdaAzoFs\n88V6zJZWe86raYLPnUWpBy+24VuRxWGFxUy8WCRkRP3rxkh/iMoRBtnX15wO\nOykKbuVOmr+Ivydhe4f4Zwbg/qnmepFLP+6eWrH92kAjNp0SrTwb0co4pihe\nJ0T8yS/VGWta38zwteTj4D7ajrhHS9dvPTSMdA+TDQq2I3j+Rvz5QeEBcJu+\nbD7TSPanKtLeMYHCzamHUu58FPSfPD3v/ZmN5tyi2rCjLNjelxv/bNyF5Xfn\nxXd96ICY7h+J5IJWTKUWzs81aUL1pyUqFm61UGhkGaRblSHZTjI+YVExdl8t\nTG5TykHS5qJHjRsykByl6Ra0Jx2Sx1QruPszUXjG5b3b7TxY/jqX3e9Xgm2b\nd27efKoS3cMtNhF+DZAWsvI8qNECwSKLlltF7TDPzlriW8vEY4nJzWwTFow+\nm7kr6fWgLdF7XQvxZ5Buv1mZ7Ne88f1nioi/zzG+fTnE32Tu3Io/xJdk/cZ4\nJ9L3wh1F+SqIP+ugxZNLyTksR02J/CDrRvq6QePE354LtS58ZB6Z35SVo21D\nzu1z08sTiD9Xil+cT49GUAvfk0Tib/19aRVd0mcrwryylkjT6Cp0jpkh/jJZ\n9Sl/ib+ighIhsQU0uLQmWg7+IfOtB4fvXeKvg0f2EJv461weEFRM/CUu3Fek\nX08hWmv861xQKE4YvbmHzMNtZbHTC7wp9Cj8Tusi/mofppt1EH/jT4QleXew\nYDEwAcZVJjRHv0XclWwHv7+izvkLzRAOjRDk0G2A/XtLeY57NUgUO8Gfq1QD\nL+bdd0aX6iFU1NzxnvgLEjLYxB/QhsZlAXO+EH+bLD1WxXOwkHJ8Ql1AsweD\nQrxz4sl+7kpjTBip9KGbpVfgQPylhC4KEnHtx63AB9Yqg2T+rV5kUhbeyjDr\nrj5dFDXA2LtevXMj8Xe8ot05nfgrWvSaO5D48w8M3XGZ+NudGPflIfHnPrFC\nH8Sf/8d7S3KIv+xfWxcVE3+RvD/yFo+yMcOvESxhyUK4e4VE8IEuHCm4tNet\ntAM2s9fMFApbITkVCN2DTTjq/fadn3stJv16v9VYl2GhfLplNj/pfx7FAbw7\ncqD/s37on3QGim+lspt100EtTf6zcTATSZw+l6MS86B3Un9g7HwJpCulXys5\nV8I+fbSR/3wD6ds3b7YSf6XcMc+Xoh2xokseTBF/y+5lnLM8yIJd003fN8Tf\nMdmiBUJWFNxneTw9yX5dbKhd/pv4WyTv8mOc+Bvt/aehEkzDpaHk3CPirzD+\nnSnnDRpPof7iAPGXartaZRNZn7lCC20kc4jQckPXXcTf/heR0n7EX596/Gwd\n8ZfX3nFOi/iT1nXwbCT+ypU9Llwk/oQ0Bdx1iD+hny8qt5C5W79upZmcEI24\nISMtI+Kv/enawFDib6ZyzaN64u/GEa85gkMk90Xte/Wd+Dsm3Oxygfi70+cv\noUD8Gda8MPQi/uTPlKkoE383rBs9eCVIfy/mnVBY3gPG9ZB2e+LvUU5Z2B3i\nr0b6nusv4q/qL72nhfhjPz670YL469rQm/qS+DvA8q+wVa6Bb/rPohnib3mY\nbYBobRMmduX/tiH+OJvCZxhCTHyuT9YaIf546o7GWhN/x4yP7gbZT675Eo3e\nxF/IMmn5SOJPc51VnDrx9+/EjqLLxN+o+MU8X+LvctG1oATib1J0oJSSbGZ4\nr1Ap/kX8PZ890fKY+FvXEJP67D9/fXqz5cTfobmxc/qIv9M8Mq6dxN8W2QeL\n+oi/DeJh3ObEXyCH2VpH4k9TfrVQOfE3FVxzNYv4U3B7NXqO+BM91pcWQfxR\nei46f4m/nw8YWwxtykCdGj6gKFCMGwalrAWqOQgRulM8I5MBn7CS2NL96fgz\ncom1digTOr8yfwYl5eHOvCoHJ/8SNOlVcbwk/tRNt9O6xF9s9Al+QUYLBuMf\nRx4g/pwO2n6Xq2MiT32t4k3izzQoJvUz8VdUKNG+mfgr+Xn7TxTZrzVZipai\nZD7dfOfE2KKTNB6F7fhlQnztcZr4VET8XR+/cVmM+BvisLjtTPwJymzs30PW\nvYRCL+wm/mbztidYEn9Ta44KxRJ/wxe/PB0i/u6XH+k9TPzF/3vzYIT4s8uV\ndblF/M3bWSdpTfx15C/U3Ev8+dJFUTrE3/bDxZoOxN/Hoj977hJ/zxL+bRkk\n/sZT+0w2EH8XDFnlC7qJuzEJw1ji772zcLUu8de9T7Q4nPg7JxXroU/8uU9c\n9VlN/LUp2sceJ/68nbr5oog/WmK92Qfiz2TD2qbV69vha31R+w/x9zprQ0kA\n8Wc3RPP9Jf5UjTXsM4m/P2LPbu4LrEdYV+FVdeKv9P7JR1eIP9W3/dr2xN+2\neWay/HNYuOV8e/Vl4q/XveZoI9nPp/LL88OIv1uT+V/uE3/79pVKGBJ/z0ti\nA58Sf08upBmaE398njuEIom//wPA8bVT\n"], {{0, 10, Rational[1, 100]}}, 1, {"Continuous", 1}, {"Discrete", 1}, 1, {ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, False, 10.2]["Values"];
ecg2 = TemporalData[
TimeSeries, {CompressedData[
"\n1:eJwllwk0Ve3/xTPmrYgiyhAaREVoUOEi4Y0GGqQoRBFNKIrQJKkUIUpSIkUZ\nkihsZBYuLtd1h3NM0WxIRdL/eX//u9Zd33XPOuusc59nP/uzt5rrMTt34SlT\npgiR7weRKVPuJPz34YAl8//TpS/uf9Nq+q3/TZMEif9NA4XfYf/NUbFVe/+b\n/q75cv9NxY9s/3gyVzcb3Ykh09yhNDqIzF1qq1SmkTnHgSUtf5uD8OpVVwtu\nkOeHjGol+ZP7jR49/aHPQZ/CpeDKqA7E80wHz1uy4cuYu+OkTBumDC92dfjS\njLKGK7a7nr9DRkibhMKtKuTsz9SrffkWlcnxn9ZbVuLoS1O9rqI6cO00njXO\nakad5Uw5lTQWEvaL0+aH2RARC/UMf87B3x+KVzan82FY87eNkdYFWTFXxQuh\nApSKXly9QP4W/v4K83aT6WKIf5oSuTGHzRgL5x3UXdmCmKqJqZ+u9KJ7xvRy\nyZ09uKCNfXr7BFgU903QOtaJ4Ny6v4UCDo4u/vX2YWEHGsRchhtl2Xh0SPx4\nbDsLIgGN4tSfZhxo/vl5cmsDlloYP1+2rAoeV49RnNQSrPjwbEx7xwtI6Oot\nHNVJxzaBtrD/1keQ3qtrXdiegYWh05g3BPnIv6V/LIBThoFKU5v3trUQnLvZ\nmebPRN9hkcHfP1uRdSSo89PHdgzdP+GvtpqD6rJUzTZ+J66vXrihb4wLk6wf\nSyOf8qCTsWk0byYf7ZYX7w5s4CPJNPzoiz18+JnE7JV24WNWQeF1wT4+Qm9O\nr3xjz0d0zzsh/S18MDNEfcvN+VjzfaXc4fV8aMbuPaGpx0fO4tmbp2jyEZL5\nMPHrfD5ETn3zH5nDx4XYnN1SUnyUTs06tVaMj14Fzt+9Ezzox8aUThnhQUHx\nxIMD/TwwuFdvNLXyIJx/5yw7nYdVJSeVDpjzYFnaEFF+mIsaj466i00cPImp\n75tuxEaNAYcl3N4KJyHL8X83MpG1Njsk07Ae9gPl/klFtTg48TXyePY7uN2J\n0HEMaYZEgebLDKM2BFlpzLW70QGvqMboKlEuavVzfFuC+Qgfdx4JWN8FaZkR\nSR/zHmTKrJ9ku3UiPKZZOPXuW8beWrmNrUZdDOb6s/0v+osZhmvWF2m3UJgv\n4XEjxO89xC+7NcyS70HQHsaCbxYUnto9U5WU4WOoPr7BdRoPx21NDRmFnYh7\nIsyJ4XWAFpe4636gHZb2uVlVO1uhWZr7IqSwCS07c2/pRtTAJkR+qv1gGd4Z\neJ7Y9rgQHjGXsz7/eYE89e1K8/kvELpvXrLivkJ8nNembEL0kJsaeKE8swaK\n6YVTr85nYrzSQauV3QpGiYt02hI2rr4+eM2X4uCX9g4dhS9cqP0OMk5x4uPR\nuXeVH2wEKKd2PWFxBUg8GpcnWEKhbPnI3q02FERnbvvsak9hWL/FU2cnBS+1\nTPMN5HqKVrd9ozGF/bO7a71XUCjaI/FNR50CLzXFXV6WQl2TQoq6OIVUvwXR\ntr8EiFQ7YJHyUQDNiIlAeb4Av69mTXvWJMC0RTtO7i4XYMu/MSnf8gQ4acF3\nzE8T4Hj+w07xWAFclb1cyv0F2LFkx4+d6wQ4MPTD+nQuHztPVlxOSeTBkA5a\n0/WsExYHhFm2VWyUTruZFaLPwsDWwJmd9UxIXRTdUuvQgEdqP0Om2jXgoatr\nsW81E+8HZ3dvNWZhMF/Sft9nNtRG30WdHO7ENbHzQa5Ez4GxnoeUVWg4mKj9\nKvvZjaUnHQoMrHowXaKJ+YzTDIttJpZVcm2MOD/TwEJHPsPPsHGHl0EZ4oaD\nRJ4f6kXYg+uvvKPeY8HaPZOqNt1Qjlz9iTpHoUDV0nq2CFnnJVeGFQd5GBqs\np4KPc7FxF31njRMHh00SKn9mtiM2wSZB1KcVXGG1uO7yJpy3/XqhIbUG+eLR\nia5e5ZD+wFI+8O0N3l2u8G6YUoDjjHLprOJCuGW89hn1L8VaXsTZJ2ZVqDRt\nMk843IAbVuIWoedaYPT5Iu2h1I6QH5UK3HUcNKWt8YnL5+JvgVpqYQQfEXY1\nqwdqBXh859qLvGgKjUM9QV+FaawNrBEXV6URab1EInYpjcDPV5PnL6fxsjG0\nzF6ThntEVuygOo3zn7bj+DwaXit9r4nPojHtVzmV8w+N1Ss27PYRojHn8ZSC\nG8MUcnrFNrt1U3hzPK7OhZwjHjWoH15O4eNIaVpLLoVJP0pNL4WCeIYl2+kW\nhdBAJeaK8xTKI+7owotCs53RogJzCnpz5z/+d1iAhaKqqf6mAtxckqBXOMDD\nd//x39sfdSLm+iOOmA8b54MTptc1tKI1+m0QI5cJp2knIx54NUJSy/BhbVcT\ntOLub12d1ALLHYab9Da2g8eYWmxWz4HK/og1dud5yJuceuROoQA5Gs0rN2zv\nglzLsIrQ/F7o5d5em5fbhc/yWdVRGgU46NTembSLz0icuNu3d6iFMUdJuExo\noB2m7r4ZHfz3+MW105VM6YPcn9s1a/y7YOZ1McwvmMIWqi+43V6AkGvVhg4a\nfJRfPXjHyJ+Lqq1LtnGWc2D77KG67KZ2rLz4ztHkQwt+trApsYRGTLhbRWx9\nWo3h/XH6Op/LIPpyq9+/PkV45Nlj5L77NSQ2Fo1HDRfjE3ak+u17iw/Lw98E\n5dWioUrC8OQ1Jp6ucLc1sWVhcXNUf3U1G4LwOg2hnE6EKuPl7WEeWkT2qlTf\nFEDWVtjJi+zHqLr4p/2LaKjY86V3bqchJXesiutBY/lVq77Xx2hsS3H+5H2U\nRlawsVcPuc6qLhX64kwjwrHUusmeRugB7fqaLTSOLPCw52ykMS96RvQUIxr1\ny6Z5Ga+kIZJq5BNN9GV6yz96guhpZZDz8iCip10ugWOSRE+nK2vnpRI9qfZ7\nXBUneloZ/SjmwVcKB49m6Nm3UvilZ2dbkkxhirzU5dcrKUg4pSjf3y6A1t+q\nvLFsHoLCuFs05TsRFaSpzk9vx8X6e07fpVtRsuzSL8qViWqTpWF5a5ow27/x\nYbFUM5jsVR/GtFlQYknN8X3PxibJGxt36HLxwkfHRDaZD4PlHh+Kyfvwg5eu\nv3i+G30vvasNw3txU9bdaqyP+P4/lqxdNsWM0pFjtxNFaEby2B/WiHYeozN8\nVdZc5S4YZtmFHE3tR4n67T2/zXtByVy86dhIw1fG7Vq3M4UZmsxL9jsE8Elk\nc5z/8MAZ5m4fmsdFKjve+p/EDlT3GsqVhbfht2/dItVpLbifp9bI5bzDNDeH\nlvGVVTjjz7TxkizD92ZFaUnHIvBc9Rd/WlSEquOnvrFqSmGjni6cMFCJbWbD\npe9y3iF1RT/zi1ILVIIrmEuYbahQPzj0R5GD5X82RjU3cNFrs0PtSjvR58/O\nVSvNiJ+Nz9HaMYdGwC2xVPe9NAy2ZH2JDKGRkv/O+1skjUN3b57XiKah4CK6\n6y35PeVByUGJcBoPPywMlSL33W7gCj06SSM6OOmmrTeNEkZy25wDNOwM4u6M\nONAwL2Nm9W+j0WjTnTVsScPksupTWQaNtIBNE9arib8sXaMUQ3zo7KkCUfZC\n4ktX/zbmK9IoX//zNS1NI74yQHfjFPLcoMvBq0DhA4+ReFqf8O1Yk2zTXAFm\nsOTPmWnwILetXnhoPQc9NgGV7qlteJX4Mmf2uhZIyK26GCDPhFVp36iwNBOy\nhwJ2d2q1YE9T1ZBOUhvspPKDy604eLv2fJ+LNQ8pMte86MsCvBRW6tKsJuuB\n/Lz593sQ/+V33McvPRCbWVtVqdYK11cZk0PMVkZEtqOfhiKPkTfZP9uA5NnS\n6hnC1mJ90By7NPXk8n44PNcJu/u+Gz0880SarIe6mFVFvy4F5W2lRV8UBWA9\n6BOyT+ChY+kKS6ULnTjednvuYBMbic9muctHs3CgQM0sdZIJT+cr98I766C4\n3sQ25E4FOit124zUSsHT2ZP91aoIVjyf1tbxYvSOKMsqR5VDeJWuiM+uGsQ4\n2/TJnm7CiZP8gXlhrRhJ3rnUR4WNYhdJXYd1nXgI+4NXXvDwyirqudYlAb6+\nWeDeWUaBylISkTen8bl19v0TQTSOni3qsIun0ZIT8CDrIY3hTkpnWgqN43dD\nl8xJorE0rn7yUhyNf67syqOu0fhySVjE7gIN1x9DJbzTNG4u2hQUcpzGuL7t\nonWHaIx9g8OMfYRHTZe7R3fQWMz9FvPDmobwukzlGRto9OV+ydZeR2Pm2+jC\n9bo0puff3nBfg8brUuZhF6KPE1J3ojrFyXXqe6ZFIQX/2QdET5O8sobh7lWR\nwceM75ohR925SNSRUlip24GVr/SkpK+yULGk9EfqkWbIvaj1zRM0oXCOiWdM\nOhNLy0sDZXa0wrpkbNh4rB0Lmp7Mvna2E2v3lscySZ6YOvW4u4MHhcSwWwZ4\n0oVrh9ruPvDrhWnLgu9BU7sRY1Q3ObP6NaTecs2OZfMYc2zeTW+0aWG4d/E3\nfo1gI7u7fDRYux8SJl4P+4b7YJfbus6yqguJa0TVgiTJusx/rtlIODgSpHqs\nrpSPZCmm75KZPExv89tuWkH6WopT1JigHfvMLbSfBbUiZdyw91NRE/pT6m0t\n62tQcHtSYDntLa7NP/0hM70EQelnZayuFMFR1X31pFQpYm44XXU5UQG9PaOK\njyvq0LnvmKbO7GasexrVmEz6TckrG7M26w6kyP29WaLPxRZFDnuaHx/ZPw+e\nGJSmYCwTmachQ/Z3yP77CjcauzuPRlyKorFMe33+kTQaOWmzbLMyybldN+BR\n+ZTGrFODGx4+opGUMefR7EQauc0apvuJjyQp1MW8Jf4RoCx5zIT4RzAj+kQb\n8Y/Qw6/CzhP/MDNxXm9J/EN//Ersgj3Ed2piEubY0mjjhFoqW9EQXC1RXEr8\nQ9/enylG/MPHcfaMesKbks+ahfeVaQT9jbRqFKHRoe0yGnWHQlda16BvgQBr\nM7M1q2X5+O554/uv052QXeGilzONjTMaoh0NJ1oheHzEsaKciaQJmSMBo014\ndi8+pcC7GYPjRUKi11i4fuHLZKRZB/QHNNIvXuPivUfF+N5xPgrELWceI+8x\n5cvEhbfPu3FPr4g3La8XskuNOQWGfNTYBheXfH/DsNA9/3l5LsVwnrv8s4Eg\nlxF5b29iuUUXciQ++T1v7EdgR3AN80gvtL1v1zX+oMH5VJf4M5vkqv0y25NT\nBMj0/FossCa8evjWM82Di4lbwovHBzog6FvS/Y3VBtqmzPTazhaclHw7uepY\nA+pSlh0R1FRhxxnOk8b7ZejIubP189li2Hz6+l5yYzGcz+s8/LCrDIXHftYZ\nn6xC1j2XRTOMGsATffGH79KC4948+rBsO9IMfRdc3c+BP33XKl+aB9USz663\nCgKEeglVVFygoDWvbWkt+f+i0ce6LgeSfcxdlLHvPo3qCN2KY89pyE8pP7M7\nh4bG8l+mj57ROJly4codohdJJYlmu3uED1+PrL17i4bS0bl+E1do3OC0LDoV\nSuNijd48CX8az4RmKOYeofGX01HlS3RXfqRRczPhlNIi7kNDOxrJJ15cMvqX\n+IfCRMM6ExqKMt3F7eR9jt1eaVVEdHFohp48j+SPOTJGa7kjFOaVpP9JOERh\nx24rym2zAPH0D0m7PTzM9yt4GHyUg01jPTY+7DbcvFt9975XCxZXHs8Js2Ki\np8s457oJEwYZcc++7WlBhlaeSk1DGxr9Y9kCfw6uy87cInaGh9U+e+Ml80kf\ns56XKSyg8XNZ5PWSlz1QX3ynfLtoL4qyrpks29IK5+BASZHUVkb0BXp/2jcu\n49W9kVce0ytQapFdkzyvD+drZ367ZdaPjMMLVC/97kZUXM3CWJLLCvUfhvbv\nofB3mDXjkrkAMr4OX8LKeLhssrC972knbiYt09rxkw2FiMHN8oUsRDuEjZou\nakbwqxrBxOJ6ZF3cJqP7vgLjA9OzdbxLUUHF1+7mFyFZl6mRf70ED6sTrTs5\n5RA5WfvueFINqOCfbntLm/C5x9fd40krquM2r/UyZYN7eTz7u2MncOORa0Mb\nDzXtxhfkHgvwaGGy1rEeChVSLb6viK9fnWeaPUB48Nl2QWByOsmdGYs+snJJ\nfvS2/Cb+guSk4hvhH4kucopjruoRXViV7nFwI34hvzBRNYv4RXJac+Esoovp\nq7te/ZdLLE4uFltwikbDCVfjJuIX318f0blF/EJ3anDaUeIXI79OG+wnfnEb\nj987Er+4UJYVbE78YnvSVbfzq0jPWSj+TZX0nV9je3L9ZWk4WZ9KX8+iIKPf\nl6mpRiF3wf0tulV8iCrzfOJDuHC41+qpSHxxyJ9f/fIRC5d+r7kucZn0xx1l\nQkESTGwV4hgElDGhu6X0Wb53K75nOLx5LMPG2RsBtTmxnUgT7M4p2MTHO5Nl\n46KhFDpe5PECX3bBv93xi3FoLwTT9qn+mdWNCTnHCmX1N2jXPyoylMBjeD/P\nLQlb3cKo6Ps6+3cyG1fGns4+tLYf6TH37uX+6cOBjnDLX8wurJOcck5WgUas\nhqRFzVSSo/W6J6+28fFDsDkxbwEP28asM+M7OHBqiHisOtKO3ZZThJJvtuLF\nOj1X794mpBhOHfUcrsH4it0BMrpvUTGbFew+WoLw5tnpCm1FWDdf9/GtlaXI\nYI9T9+MqYLYlWSfkQx3Gj+iOexFdxXEP++QOsOB5YXNTvlMHDh9QVfLdyMVO\n+cbCqEt8eAcOvdikTkFJ+pRYyVySp6KZg9lk31y+K54fTCA+kWc9u4L4xN97\nCU8H80hOdP6YOEL0MVHo6lhEeHJD/J+kuYQjNuv/1m27Q0NPsrI7+SYNsaRD\nef9cprGFHdsVcZb0GGPm9oV+JIesL7zddpiGm9nBl0kuZN73fhK8m8aZG5UK\nPltpcKtjq7wtaGid3+quT3rL4JnFdr16NELEZx18TPLnpJz8y4ppNCqaEzUc\n0yn4BTYvn1clwG3Tf5Vs1fnw0mNKOF/uRLpZ68wf8mzQkfv0h4Nb0Rjw8XVl\nExN+6Qr70qcy0bEvZGfg6WbkJJ8zTYtnQVyF1TVrawdWla8W64/n4rpSW9BD\ncQH6B1WSzhkSjhZXRdbldUPl0vYtk4W9KPDNeeZvxUe4o3CDVtUbRrq5Z/HT\nNIpBL5LMjs/OZQSdPDvH26YLnZb+eRtZ/bi3OHfzHt9etJutv28xQfLa9Q+H\nm95Q8NjU77PnuQB6s3YdOLuLj/n6Fru1fLlIOFtreGCE8EOjzNyIaoOkrUs1\n9rfgb+RmKdcLDfConCjv5FWhMeyeddyLMixZa/9tcWoxMnd/jun3KsZxdkqt\n9uEymHsdibMIr4LH5Hvfnq0N6Fkgr6hFfNMgLLojXrkdZ0Z0rJ57cLCy92hx\nxVwe7lYUvHijJkBSpV9s2jUKp095vFm+nobRzazoLnK+PWWfdGSSXBkxITee\nS3TwcL4+L+ol6Y/tlByLcMT6/JHRUpIvvp1yrzn6gIa/jHJh5m2SS69RcSKk\nnyw26BLzvUhjyOFH8/gZkqtGpCvunKCx3lAv0I70Wa9wORH1/UQn4u9fT91F\nE52be0/a0OjWrXUfIrnztLbal3Mkd6bgj5uTDskrW2/o+qkQH7o8r3xsnMLg\n8pLE1KMU3A7+cnAjvS70Y+JpMxceVuZ6uzqd5KBo9RuKIWjDavuwXEefFqzY\nfyZJbysTsyTGopZbMhHadlYskPBVIzi315xwuy13T7tNMAc3TBMy94XyEJpO\npe0qEqB0bmrXwi4aT02WX2sr6MEziwA316m96BnyktYlOVXvIXPfzPutjF1G\nG3LxgcsQFUrzlJGvwL4P9TtDlfvQevrh3mMb+8EKHp7vMNkNvw0/6/eTdej5\nMWLoS3qpWJ39daFNAuz88OHcjyoeJvXFAi2zO8FZdKIhfYINjxw+va+EhcoK\nj7SzWs0Q0bululu3Hhzp/JN+gxUImO3F8zxVCrdJ5+grQ0VQ8KmNffygBPkP\nHo0+6SnH8UiW1Or0Gniumv9VqK4J5bsfvF/0nPT05ZXdUhZsqJzaGXHfpROl\nm4dCvTt5GC1zy87IEGCdxD+CX/0UQjlOh0fJ/jBV8jaq3iDn0uCsSQvZd3Pl\nH+pTiB4EPqMTy8iUllMpmJ5NY3brHNcthC9SG9jMM6SPdHc9sSiNocFSmbir\ncpXGy8krB2LP0Tg3L/vywgAaA+vfPaonPLWvUbgc4U70YcX+7exI+un+pts2\n20nv8HztvHETjX27ghSXmNL43fVc12UNjVs3ncfGtUgevRQmtpn0Zk/Tkz95\nbNLnXl8sLltIgZ3ydk1pLR8XSt9Yq1zgItDqkGX8lg7IruFXaqazYPy5Eb4R\nzbDqeO0rmM6EseoL65YKJhTsG/5MPd4Kp7lIG5RlI/PDL53h+E7MXLPMfWgz\nHwtf3ptcSfKWfJFV38xXXfhoxuY0nuvFbqcY6Suy3ej96SRw0n6DgbT+jIE4\nHmPcfDEjTL+F8arLbXIkhY3ZC48/otb1wz4sNkXjbx+e2mcFerZ0wbyyrvEc\n8WWxEzpv706jsOJ1yqbdHXw4mwvVnV7Mw+Kzyq93cTnQSpXKY4+2QywkZ8O2\nW60YuPcapR+awHFdx3v+swan7Uzc/l39Ft4PwtYX/y1BTYDB9h1UEQL0Vqum\nri3FGR39Ryl3K3BY+XXvya91MOiNY3dpNCN0zhLRBZ9YqL84w1HVuQN1tJE2\ny5KL7w3l+79c5iNGNrUuiaxrgHFOQh/JcdGcla1tJA/S/OzuWXdpXEnqzerO\nIn3DwZY9LZ+GsuOCgH8IR2a+5j1qJLmi0PuO75JU4gtzM746kvvLth7b+5T0\nlqNdzHBp0kO2WZxXuBFMI02kb2QR6SFPSmMes7xoGC6dZnjXlYbp46DMANLb\no66Z3ffcRmO+szPbxZLk2L4WscXGNLKND1xh6RO/2vTdIHYRjQIPG63s6YRf\n9z66aD+lMD71a0V/tQCMklileQv5+GoWHrTwSifyGQbC+XPZcP2cm/sstBXe\n/isag5qZkDv/ZfXef5igz7ZCM7AZa+Zvd952h4V/VucXFGzrgIjD18fhd7go\nb5+vYSIhgO9l+c1bCMfK2rMXxb7sxtdczZGq170wV9KdECW5o9R7noFY6RuG\n+oFZmxalUgxpI23L6Ke5DPvm8AGtzV1INt54T7itH9jcc0+O9NmowrSyv4Qf\ng96/ZI2LKRy4NtejMkuAl4HTy3rt+Xhq9Fk90o+LTRcXe7/93oFblyP+JNBt\n6H4XoT6X+Fr0PqcDUmEN+LLzqkcoVYW6WxzVVfllyC5v6bB7WozvHWMXpp4o\nhluR9uoC7zI0P/PKr42ogmh+721nuwasPfqL6+bdgt3lCe8bVdphwdtg3+PJ\nQdY+g9c/5/EgF7Fdf0BdgKHep/nM6xSkupxRRvjByHP47Et6g9IhWb4RyQu3\nD3dlmJJ8ubPh71wVoouJt12tToQnnSMRI5YZND5FKe39TvghrxPzc0U8yRXj\nQRfDCD8WPvuZ+p3wQ0i5WyOQ9JniHKnWuT40Kr/csmASfqSZKUYmEX4kzG+T\nuED8SUZ7LDRgM8mhjDkbDpvTiJ8fHzdG+DHm0Mpv/Y8fUx8EfSD8+FJ9Rbj7\nNwULz8fXrx6jcNFwuZDVTgHk1DbzF7jyYJR48LLhKQ7+jK15p0R4fG6T75E1\nvi34oJKvOX0bE+NJWRMipIf0st5bb3VtwZoN22bKt7WhcEGwQCmEg/AHcrnL\nzvEQeV/rmXqxAKz0o21XCD9uwur82sIePH76ZXcl4UfwVlmhUcIPafmuvZuT\nWhlMy7Uv/w5wGYLy+23XFSqQnSZ/QkD4sSvjQcQ7wo+Ap15BLwk/hKoyFr0h\n/EhvU5Vc4kJB1MAsMo/w483zrpLH1Tx4Zs0Y/EH4EZ/78uyuP2z8DUvpmQYW\nDPdmTmosbYb6N++ZT/TqUcux9SsbqoCw4lb7F/6lWLHMvFz+exE+j5je0XlU\ngslwq9GPveXQ9kmifJ/U4LWGRaphfRPUFi/0fEv4UU/n2mYSfmwd6pdd69qJ\nKT+GS4W5PHjH3NYzzhSgXfDsR8QAhSjRe6LG9jQCm9nVhwg/NpzVb1Ug++5c\nRkVuJNx4fDfh2HEyPx1kUDaEH2dFmJ6RhB//B6JZ5o8=\n"], {{0, 10, Rational[1, 100]}}, 1, {"Continuous", 1}, {"Discrete", 1}, 1, {ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, False, 10.2]["Values"];
ListLinePlot[{ecg1, ecg2}, PlotRange -> Full, AxesLabel -> {"time (s)", "voltage (mV)"}, DataRange -> {0, 10}, ImageSize -> 400]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/2e6c57b2e12fbeea.png) |
| Out[16]= | 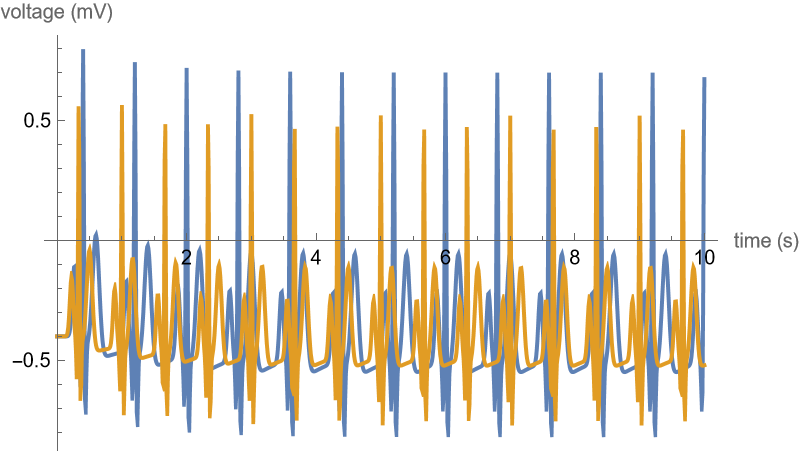 |
| In[17]:= | ![m = 2;
r1 = 0.2*StandardDeviation[ecg1];
r2 = 0.2*StandardDeviation[ecg2];
{ResourceFunction["SampleEntropy"][ecg1, m, r1], ResourceFunction["SampleEntropy"][ecg2, m, r2]}](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/1cd14f369d0fc3a5.png) |
| Out[18]= |
Sample entropy of a linearly increasing time series is zero:
| In[19]:= | ![ts = Range[10000];
m = 2; r = 0.2*StandardDeviation[ts];
ResourceFunction["SampleEntropy"][ts, m, r]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/7b0f5b2a49d9101d.png) |
| Out[20]= |
Sample entropy of a pure sine wave:
| In[21]:= | ![data = N@Sin[2*Pi*Range[3000]/100];
m = 2; r = 0.2*StandardDeviation[data];
ResourceFunction["SampleEntropy"][data, m, r]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/79103901524ee5b5.png) |
| Out[15]= |
Sample entropy of a time series sampled from a normal distribution:
| In[22]:= | ![SeedRandom[1234567];
datanorm = RandomVariate[NormalDistribution[], 10000];
m = 2; r = 0.2*StandardDeviation[datanorm];
ResourceFunction["SampleEntropy"][datanorm, m, r]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/48225d8e03eba559.png) |
| Out[23]= |
Sample entropy of gaussian fractional noise with Hurst exponential H = 0.5:
| In[24]:= | ![SeedRandom[42];
samplenoise = Flatten@RandomFunction[
FractionalGaussianNoiseProcess[.5], {1, 10000, 1}]["ValueList"];
m = 2; r = 0.2*StandardDeviation[samplenoise];
ResourceFunction["SampleEntropy"][samplenoise, m, r]](https://www.wolframcloud.com/obj/resourcesystem/images/500/5008f976-f5b8-4f27-9efb-4806b8a0fcdf/5b3c7dd6618d9fb3.png) |
| Out[25]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License