Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RollingCurve

Source Notebook

Compute a rolling curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["RollingCurve"][c,r,h,t0,t]

gives the parametrized curve traced out by a point P attached to a circle of radius r rolling along a plane curve c parametrized by variable t. The distance from P to the center of the rolling circle is h, and t0 is the point of the curve at which the circle starts rolling.

ResourceFunction["RollingCurve"][c,r,t0,t]

takes the distance from the tracing point to the center of the rolling circle to be Abs[r].

Details

A rolling curve is also referred to as a roulette.
Rolling curves have been extensively studied for many applications in mechanical engineering.

Examples

Basic Examples (3) 

Define the parametric equations for an ellipse:

In[1]:=
ellipse[a_, b_][t_] = Entity["PlaneCurve", "Ellipse"]["ParametricEquations"][a, b][t]
Out[1]=

Compute the rolling curve of the ellipse:

In[2]:=
rce = ResourceFunction["RollingCurve"][ellipse[2, -1][t], 1, 1, 0, t]
Out[2]=

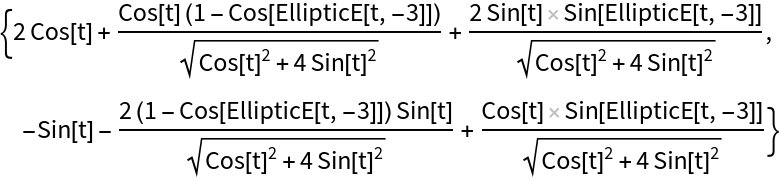
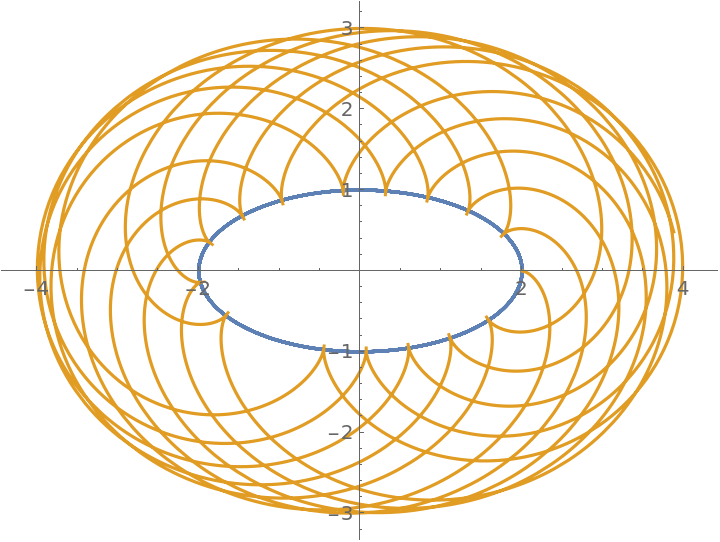
Plot the rolling curve:

In[3]:=
ParametricPlot[Evaluate[{ellipse[2, -1][t], rce}], {t, 0, 20 \[Pi]}, Exclusions -> None]
Out[3]=

Scope (4) 

Parametric equations for a circle:

In[4]:=
circle[t_] := {Cos[t], Sin[t]}

The epitrochoid is the rolling curve of a circle if the rolling circle is outside the original circle:

In[5]:=
ResourceFunction["RollingCurve"][{Cos[t], Sin[t]}, -r, h, 0, t] // Simplify
Out[5]=

The epicycloid is obtained if :

In[6]:=
ResourceFunction["RollingCurve"][{Cos[t], Sin[t]}, -1/3, 1/3, 0, t] // Simplify
Out[6]=

An equivalent way to get the epicycloid:

In[7]:=
ResourceFunction["RollingCurve"][{Cos[t], Sin[t]}, -1/3, 0, t] // Simplify
Out[7]=

Properties and Relations (5) 

Define the parametric equations of a parabola:

In[8]:=
parabola[a_][t_] = Entity["PlaneCurve", "Parabola"]["ParametricEquations"][a][t]
Out[8]=

Define the rolling curve of the parabola:

In[9]:=
paracyc[r_, h_, t_] = ResourceFunction["RollingCurve"][parabola[1][t], r, h, 0, t]
Out[9]=

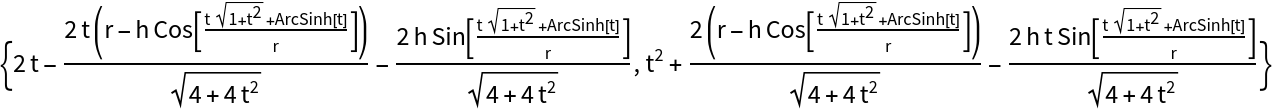
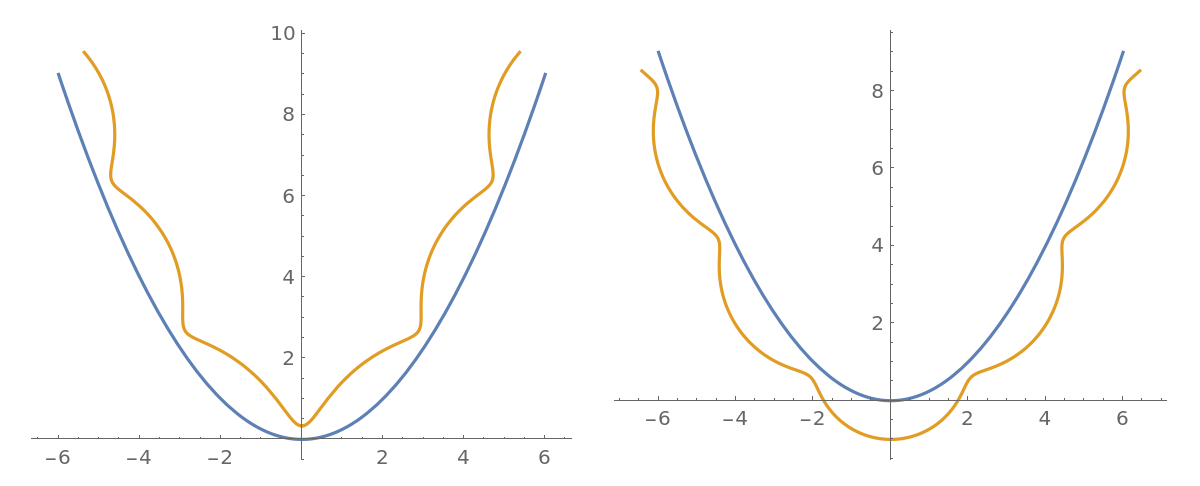
When (the curtate case), the rolling curve is smooth:

In[10]:=
GraphicsRow[{ParametricPlot[{parabola[1][t], paracyc[2/3, 1/3, t]}, {t, -3, 3}], ParametricPlot[{parabola[1][t], paracyc[-2/3, 1/3, t]}, {t, -3, 3}]}]
Out[10]=

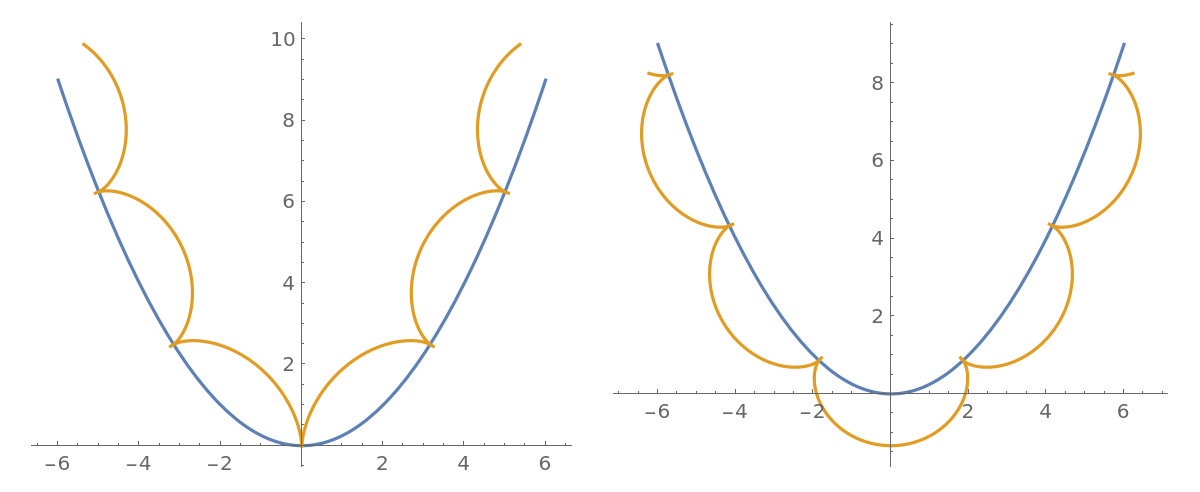
When (the cycloidal case), the rolling curve has cusps:

In[11]:=
GraphicsRow[{ParametricPlot[{parabola[1][t], paracyc[2/3, 2/3, t]}, {t, -3, 3}], ParametricPlot[{parabola[1][t], paracyc[-2/3, 2/3, t]}, {t, -3, 3}]}]
Out[11]=

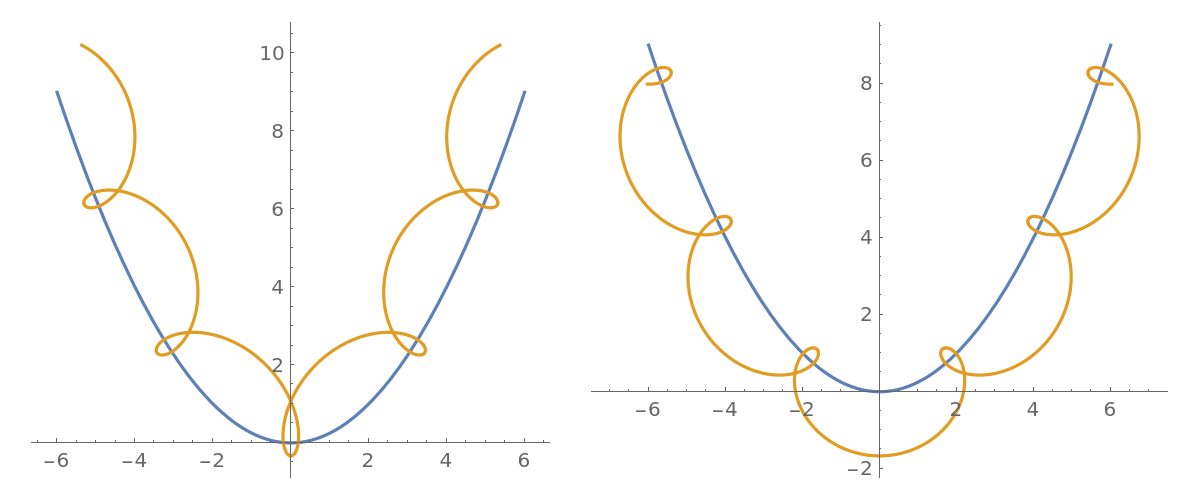
When (the prolate case), the rolling curve has self-intersection points:

In[12]:=
GraphicsRow[{ParametricPlot[{parabola[1][t], paracyc[2/3, 1, t]}, {t, -3, 3}], ParametricPlot[{parabola[1][t], paracyc[-2/3, 1, t]}, {t, -3, 3}]}]
Out[12]=

Neat Examples (4) 

Define the parametric equations of a trochoid:

In[13]:=
trochoid[a_, b_][t_] = Entity["PlaneCurve", "Trochoid"]["ParametricEquations"][a, b][t]
Out[13]=

Compute the parallel curve of the trochoid:

In[14]:=
par = ResourceFunction["ParallelCurve"][trochoid[2, 1][t], 1, t] // Simplify
Out[14]=

Compute the rolling curve of the trochoid:

In[15]:=
rcc = ResourceFunction["RollingCurve"][trochoid[2, 1][t], 1, 0, t] // Simplify
Out[15]=

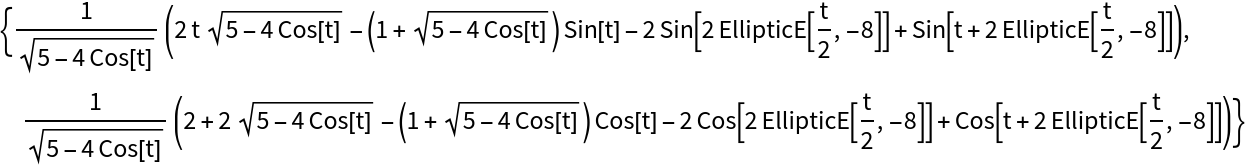
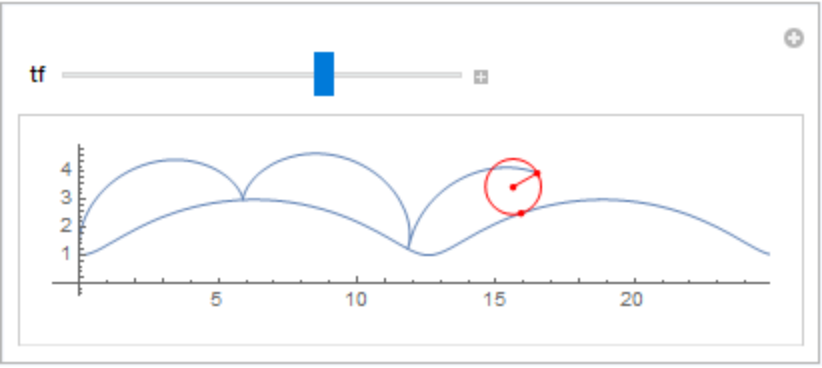
Create a Manipulate that rolls a circle along the curve:

In[16]:=
Manipulate[ Show[ParametricPlot[Evaluate[rcc], {t, 0, tf}, Epilog -> {Directive[Red, PointSize[0.01]], Circle[par /. t -> tf], Line[{par /. t -> tf, rcc /. t -> tf}], Point[{trochoid[2, 1][tf], par /. t -> tf, rcc /. t -> tf}]}, Axes -> True, PlotRange -> {{-0.96, 24.85}, {-.5, 4.98}}], ParametricPlot[Evaluate[trochoid[2, 1][t]], {t, 0, 4 \[Pi]}]], {{tf, 8.4}, .01, 4 \[Pi]}]
Out[16]=

Publisher

Enrique Zeleny

Version History

  • 1.0.1 – 29 March 2021
  • 1.0.0 – 28 February 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information