Function Repository Resource:

RiemannTensor (1.0.0) current version: 2.0.0 »

Source Notebook

Compute the components of the Riemann tensor for a metric

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["RiemannTensor"][M,{u,v}]

computes the Riemann tensor Rⁱ_jkl for the metric M.

Details and Options

A Riemann tensor is a four-index tensor that is used commonly in general relativity.

The Ricci curvature tensor and scalar curvature can be defined in terms of Rⁱ_jkl.

The Riemann tensor can be constructed from the metric tensor and its first and second derivatives via

where the

s are Christoffel symbols of the first kind.

Examples

Basic Examples (6)

The monkey saddle surface:

In[1]:=

$monkeysaddle[u_, v_] := {u, v, u^3 - 3 u v^2} ms = monkeysaddle[u, v]$

Out[2]=

Plot the surface:

In[3]:=

$ParametricPlot3D[{u, v, u^3 - 3 u v^2}, {u, -\[Pi], \[Pi]}, {v, -\[Pi], \[Pi]}, BoxRatios -> {1, 1, 1}, PlotRange -> All]$

Out[3]=

The covariant basis:

In[4]:=

${Subscript[g, \[Alpha]], Subscript[g, \[Beta]]} = Transpose@(D[{u, v, u^3 - 3 u v^2}, {{u, v}}])$

Out[4]=

The metric tensor:

In[5]:=

$Subscript[g, \[Alpha]\[Beta]] = SymmetrizedArray[{{1, 1} -> Subscript[g, \[Alpha]] . Subscript[g, \[Alpha]], {1, 2} -> Subscript[g, \[Alpha]] . Subscript[g, \[Beta]], {2, 2} -> Subscript[g, \[Beta]] . Subscript[g, \[Beta]]}, {2, 2}, Symmetric[{1, 2}]] // Simplify$

Out[5]=

All the components of the Riemann tensor with one upper index:

In[6]:=

$(rtcov = FullSimplify[ ResourceFunction["RiemannTensor"][Subscript[ g, \[Alpha]\[Beta]], {u, v}]]) // MatrixForm$

Out[6]=

Using TensorIndexJuggling to lower the first index to get R_ijkl:

In[7]:=

$ResourceFunction["TensorIndexJuggling"][\!$\* TagBox["rtcov", Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]$, \!$\* TagBox[ RowBox[{"(", "", TagBox[GridBox[{ { RowBox[{"1", "+", RowBox[{"9", " ", SuperscriptBox[ RowBox[{"(", RowBox[{ SuperscriptBox["u", "2"], "-", SuperscriptBox["v", "2"]}], ")"}], "2"]}]}], RowBox[{ RowBox[{"-", "18"}], " ", "u", " ", "v", " ", RowBox[{"(", RowBox[{ SuperscriptBox["u", "2"], "-", SuperscriptBox["v", "2"]}], ")"}]}]}, { RowBox[{ RowBox[{"-", "18"}], " ", "u", " ", "v", " ", RowBox[{"(", RowBox[{ SuperscriptBox["u", "2"], "-", SuperscriptBox["v", "2"]}], ")"}]}], RowBox[{"1", "+", RowBox[{"36", " ", SuperscriptBox["u", "2"], " ", SuperscriptBox["v", "2"]}]}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]$, From -> {"Con", "Cov", "Cov", "Cov"}, To -> "AllCovariant"] // FullSimplify // MatrixForm$

Out[7]=

Properties and Relations (3)

The metric tensor for the monkey saddle:

In[8]:=

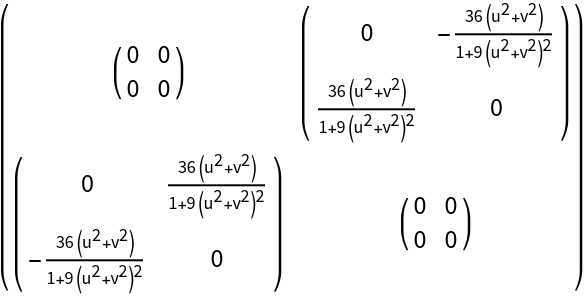
$Subscript[g, \[Alpha]\[Beta]] = StructuredArray[ SymmetrizedArray, {2, 2}, StructuredArray`StructuredData[ SymmetrizedArray, {{1, 1} -> 1 + 9 (u^2 - v^2)^2, {1, 2} -> (-18) u v (u^2 - v^2), {2, 2} -> 1 + 36 u^2 v^2}, Symmetric[{1, 2}]]];$