Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the resistance matrix of a graph
ResourceFunction["ResistanceMatrix"][g] gives the resistance matrix of the graph g. |
Compute the resistance matrix of the tetrahedral graph:
| In[1]:= |
| Out[1]= |
Compare with the result of GraphData:
| In[2]:= |
| Out[2]= |
Compute the resistance matrix of the dodecahedral graph:
| In[3]:= | ![AbsoluteTiming[rm = ResourceFunction["ResistanceMatrix"][\!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{{0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {0, 7}, {0, 8}, {0, 9}, {0, 10}, {0, 11}, {0, 12}, {0, 13}, {0, 14}, {
0, 15}, {0, 16}, {0, 17}, {0, 18}, {0, 19}, {0, 20}}, {Null,
SparseArray[
Automatic, {20, 20}, 0, {1, {{0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60}, {{14}, {15}, {16}, {
5}, {6}, {13}, {7}, {14}, {19}, {8}, {15}, {20}, {2}, {
11}, {19}, {2}, {12}, {20}, {3}, {11}, {16}, {4}, {
12}, {16}, {10}, {14}, {17}, {9}, {15}, {18}, {5}, {
7}, {12}, {6}, {8}, {11}, {2}, {17}, {18}, {1}, {3}, {
9}, {1}, {4}, {10}, {1}, {7}, {8}, {9}, {13}, {19}, {
10}, {13}, {20}, {3}, {5}, {17}, {4}, {6}, {18}}}, Pattern}]}, {VertexCoordinates -> CompressedData["
1:eJxTTMoPSmViYGAQAWJmIK5cXcyzkvXbfgYo4A1eyHvq0gV7qLg9mvj+J8xu
3B0Wt/eH/Dp9dvfHL/th6tHE7WHiW8O4O79d+Gi/4sv02eWPX+7HIQ5XD7MH
ph6mDk0crh/izmdQ9z/Yvw0ivh9N3B5N3B6mHs0cmDjc/Kdgf72GhwPMHBiN
5i90cXvUcHsND2c0f8HDB6YfTRzufmg426OFP7o43F4AXY3xjw==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJxTTMoPSmViYGAQAWJmIK5cXcyzkvXbfgYo4A1eyHvq0gV7qLg9mvj+J8xu
3B0Wt/eH/Dp9dvfHL/th6tHE7WHiW8O4O79d+Gi/4sv02eWPX+7HIQ5XD7MH
ph6mDk0crh/izmdQ9z/Yvw0ivh9N3B5N3B6mHs0cmDjc/Kdgf72GhwPMHBiN
5i90cXvUcHsND2c0f8HDB6YfTRzufmg426OFP7o43F4AXY3xjw==
"], {
{Hue[0.6, 0.2, 0.8], Arrowheads[0.], Arrow3DBox[TubeBox[{{1, 14}, {1, 15}, {1, 16}, {2, 5}, {
2, 6}, {2, 13}, {3, 7}, {3, 14}, {3, 19}, {4, 8}, {4, 15}, {4, 20}, {5, 11}, {5, 19}, {6, 12}, {6, 20}, {7, 11}, {7, 16}, {8, 12}, {8, 16}, {9, 10}, {9, 14}, {9, 17}, {10, 15}, {10, 18}, {11, 12}, {13, 17}, {13, 18}, {17, 19}, {18, 20}}], 0.05687975353745206]},
{Hue[0.6, 0.6, 1], SphereBox[1, 0.05687975353745206], SphereBox[2, 0.05687975353745206], SphereBox[3, 0.05687975353745206], SphereBox[4, 0.05687975353745206], SphereBox[5, 0.05687975353745206], SphereBox[6, 0.05687975353745206], SphereBox[7, 0.05687975353745206], SphereBox[8, 0.05687975353745206], SphereBox[9, 0.05687975353745206], SphereBox[10, 0.05687975353745206], SphereBox[11, 0.05687975353745206], SphereBox[12, 0.05687975353745206], SphereBox[13, 0.05687975353745206], SphereBox[14, 0.05687975353745206], SphereBox[15, 0.05687975353745206], SphereBox[16, 0.05687975353745206], SphereBox[17, 0.05687975353745206], SphereBox[18, 0.05687975353745206], SphereBox[19, 0.05687975353745206], SphereBox[20, 0.05687975353745206]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
BaseStyle->{Graphics3DBoxOptions -> {Method -> {"ShrinkWrap" -> True}}},
Boxed->False,
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\)];]](https://www.wolframcloud.com/obj/resourcesystem/images/6a3/6a3fc04f-e536-4cd0-a231-ef3c5923ae9f/797811929ae2bd2a.png) |
| Out[3]= |
Get all the unique resistance distances:
| In[4]:= |
| Out[4]= |
Compute the resistance matrix of a large graph:
| In[5]:= |
| Out[5]= |
Visualize the resistance matrix:
| In[6]:= |
| Out[6]= | 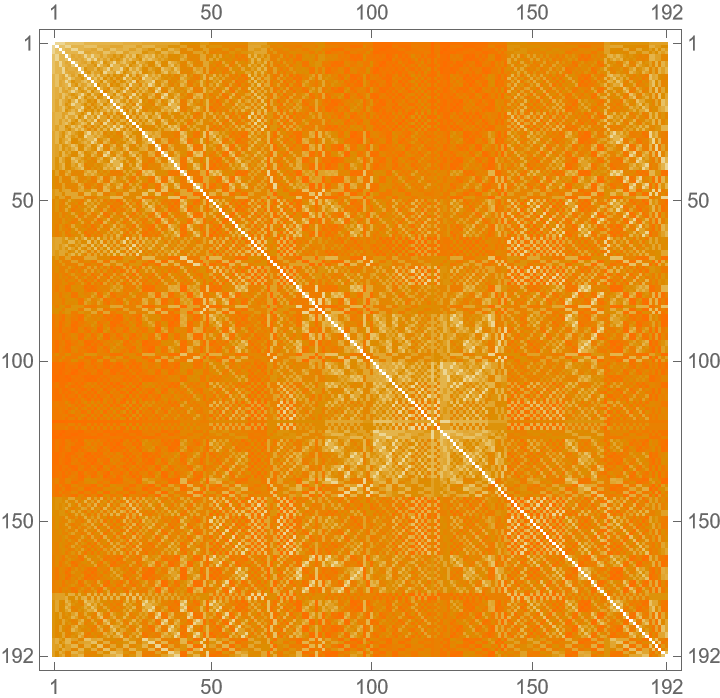 |
A graph:
| In[7]:= | ![gg = \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}, {Null, {{1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}, {6, 7}, {7, 8}, {8, 9}, {9, 10}, {10, 11}, {11, 12}, {12, 13}, {
13, 14}, {14, 15}, {15, 16}, {16, 17}, {16, 18}, {18, 19}, {
19, 20}, {8, 1}, {18, 9}, {20, 2}, {7, 3}, {20, 9}, {19, 4}, {18, 6}, {17, 10}, {20, 12}, {17, 13}, {19, 14}}}, {AnnotationRules -> {5 -> {"AtomicNumber" -> 6}, 4 -> {"AtomicNumber" -> 6}, 12 -> {"AtomicNumber" -> 6}, UndirectedEdge[1, 2] -> {"BondOrder" -> "Single"}, UndirectedEdge[8, 9] -> {"BondOrder" -> "Single"}, UndirectedEdge[12, 13] -> {"BondOrder" -> "Single"}, UndirectedEdge[13, 14] -> {"BondOrder" -> "Single"}, 10 -> {"AtomicNumber" -> 6}, UndirectedEdge[11, 12] -> {"BondOrder" -> "Single"}, 18 -> {"AtomicNumber" -> 6}, 11 -> {"AtomicNumber" -> 6}, UndirectedEdge[17, 13] -> {"BondOrder" -> "Single"}, UndirectedEdge[16, 17] -> {"BondOrder" -> "Single"}, 3 -> {"AtomicNumber" -> 6}, 6 -> {"AtomicNumber" -> 6}, UndirectedEdge[6, 7] -> {"BondOrder" -> "Single"}, UndirectedEdge[9, 10] -> {"BondOrder" -> "Single"}, 1 -> {"AtomicNumber" -> 6}, UndirectedEdge[20, 9] -> {"BondOrder" -> "Single"}, UndirectedEdge[7, 8] -> {"BondOrder" -> "Single"}, 17 -> {"AtomicNumber" -> 6}, 15 -> {"AtomicNumber" -> 6}, 2 -> {"AtomicNumber" -> 6}, 14 -> {"AtomicNumber" -> 6}, UndirectedEdge[10, 11] -> {"BondOrder" -> "Single"}, 13 -> {"AtomicNumber" -> 6}, UndirectedEdge[8, 1] -> {"BondOrder" -> "Single"}, UndirectedEdge[19, 14] -> {"BondOrder" -> "Single"}, UndirectedEdge[17, 10] -> {"BondOrder" -> "Single"}, 16 -> {"AtomicNumber" -> 6}, UndirectedEdge[19, 4] -> {"BondOrder" -> "Single"}, UndirectedEdge[5, 6] -> {"BondOrder" -> "Single"}, UndirectedEdge[16, 18] -> {"BondOrder" -> "Single"}, UndirectedEdge[4, 5] -> {"BondOrder" -> "Single"}, UndirectedEdge[15, 16] -> {"BondOrder" -> "Single"}, UndirectedEdge[3, 4] -> {"BondOrder" -> "Single"}, UndirectedEdge[18, 9] -> {"BondOrder" -> "Single"}, UndirectedEdge[20, 12] -> {"BondOrder" -> "Single"}, 20 -> {"AtomicNumber" -> 6}, UndirectedEdge[18, 6] -> {"BondOrder" -> "Single"}, 8 -> {"AtomicNumber" -> 6}, UndirectedEdge[19, 20] -> {"BondOrder" -> "Single"}, UndirectedEdge[18, 19] -> {"BondOrder" -> "Single"}, UndirectedEdge[20, 2] -> {"BondOrder" -> "Single"}, 7 -> {"AtomicNumber" -> 6}, UndirectedEdge[2, 3] -> {"BondOrder" -> "Single"}, 9 -> {"AtomicNumber" -> 6}, UndirectedEdge[14, 15] -> {"BondOrder" -> "Single"}, UndirectedEdge[7, 3] -> {"BondOrder" -> "Single"}, 19 -> {"AtomicNumber" -> 6}}, GraphLayout -> {"Dimension" -> 3, "VertexLayout" -> "SpringElectricalEmbedding"}}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJxTTMoPSmViYGAQAWJmIHbke1P8W5HLgQEKrtzOqBaPfmBvJnZha0Abm0Pd
7Gfawe0P7RkChP+xW9raO1zgq5Wew+WgUVH5+c6Wr/YX9u8/9Zt5h/2hfwx7
61vZHKpi/C7MCGaEm/erc8GJSQpcDlt0gjP+bWV1mMDJM1ku/IH9rJVnztxs
Z3OwaHNeOymE0SHyNXdLa8wHex3W8LfngebPVNG//HHbV3sfGS6pxXve2tfZ
C12fBnSPp+/5vPaOh/ZME3UqHIHq1zvdYVSf/cuesWPV8T0mr+zLGuf+Phjw
zr7J06boYOAD+45Nu6ZebX5onzdn2ROQ+QkvWor3n1tnz9Dg+1okhMtefXbt
hfqIB/ZhN/jKE0Mf2Isbf+O/0gj074vjz1y77YHqhKJmLjK2/7VzURHr9q/2
Cy5wlhZ+3W6/bnVChFXYA3u9r98UHgPdz3DAKFNmApf9gdmzvKw41ts3pUZn
bdrG6sCQvzaYJ/aB/RQmlnsiQHumnZb//RuofqvI/+umsR/sYeHkbHLp8NGt
X+0tsp9sfwb075OwnZI7Zv2yP8I4v6zR9599kn/qjp2B7+wDj5zraAaKi3zJ
DEjy+2dfs1P6TlT0Zvuf4gemsALFF8gxK0dbvbLf4dDVfsBpsz0AtavYKQ==
"], {
{Hue[0.6, 0.2, 0.8], Arrowheads[0.], Arrow3DBox[TubeBox[{{1, 2}, {1, 8}, {2, 3}, {2, 20}, {3, 4}, {3, 7}, {4, 5}, {4, 19}, {5, 6}, {6, 7}, {6, 18}, {7,
8}, {8, 9}, {9, 10}, {9, 18}, {9, 20}, {10, 11}, {10, 17}, {11, 12}, {12, 13}, {12, 20}, {13, 14}, {13, 17}, {
14, 15}, {14, 19}, {15, 16}, {16, 17}, {16, 18}, {18, 19}, {19, 20}}], 0.06507303815546206]},
{Hue[0.6, 0.6, 1], SphereBox[1, 0.06507303815546206], SphereBox[2, 0.06507303815546206], SphereBox[3, 0.06507303815546206], SphereBox[4, 0.06507303815546206], SphereBox[5, 0.06507303815546206], SphereBox[6, 0.06507303815546206], SphereBox[7, 0.06507303815546206], SphereBox[8, 0.06507303815546206], SphereBox[9, 0.06507303815546206], SphereBox[10, 0.06507303815546206], SphereBox[11, 0.06507303815546206], SphereBox[12, 0.06507303815546206], SphereBox[13, 0.06507303815546206], SphereBox[14, 0.06507303815546206], SphereBox[15, 0.06507303815546206], SphereBox[16, 0.06507303815546206], SphereBox[17, 0.06507303815546206], SphereBox[18, 0.06507303815546206], SphereBox[19, 0.06507303815546206], SphereBox[20, 0.06507303815546206]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
BaseStyle->{Graphics3DBoxOptions -> {Method -> {"ShrinkWrap" -> True}}},
Boxed->False,
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}},
ViewPoint->{-1.416849149524804, 0.3059078201308579, -3.0576067263586446`},
ViewVertical->{-0.8523851455933351, -0.003400704808721405, -0.5229034315995953}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/6a3/6a3fc04f-e536-4cd0-a231-ef3c5923ae9f/168f6b49cb30734e.png) |
Define a function for computing the Kirchhoff index:
| In[8]:= |
Compute the Kirchhoff index:
| In[9]:= |
| Out[9]= |
Define a function for computing the Kirchhoff sum index:
| In[10]:= | ![KirchhoffSumIndex[g_?ConnectedGraphQ] := Module[{gd, om},
gd = SparseArray[LowerTriangularize[GraphDistanceMatrix[g]]];
om = SparseArray[
LowerTriangularize[ResourceFunction["ResistanceMatrix"][g]]];
Total[om["ExplicitValues"]/gd["ExplicitValues"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a3/6a3fc04f-e536-4cd0-a231-ef3c5923ae9f/00707ddd5ba2d5f7.png) |
Compute the Kirchhoff sum index:
| In[11]:= |
| Out[11]= |
Visualize the resistance matrices of the Archimedean graphs:
| In[12]:= | ![Partition[
MatrixPlot[ResourceFunction["ResistanceMatrix"][GraphData[#]], PlotLabel -> GraphData[#, "Name"]] & /@ GraphData["Archimedean"],
UpTo[5]] // GraphicsGrid](https://www.wolframcloud.com/obj/resourcesystem/images/6a3/6a3fc04f-e536-4cd0-a231-ef3c5923ae9f/297032656dd3f84f.png) |
| Out[12]= | 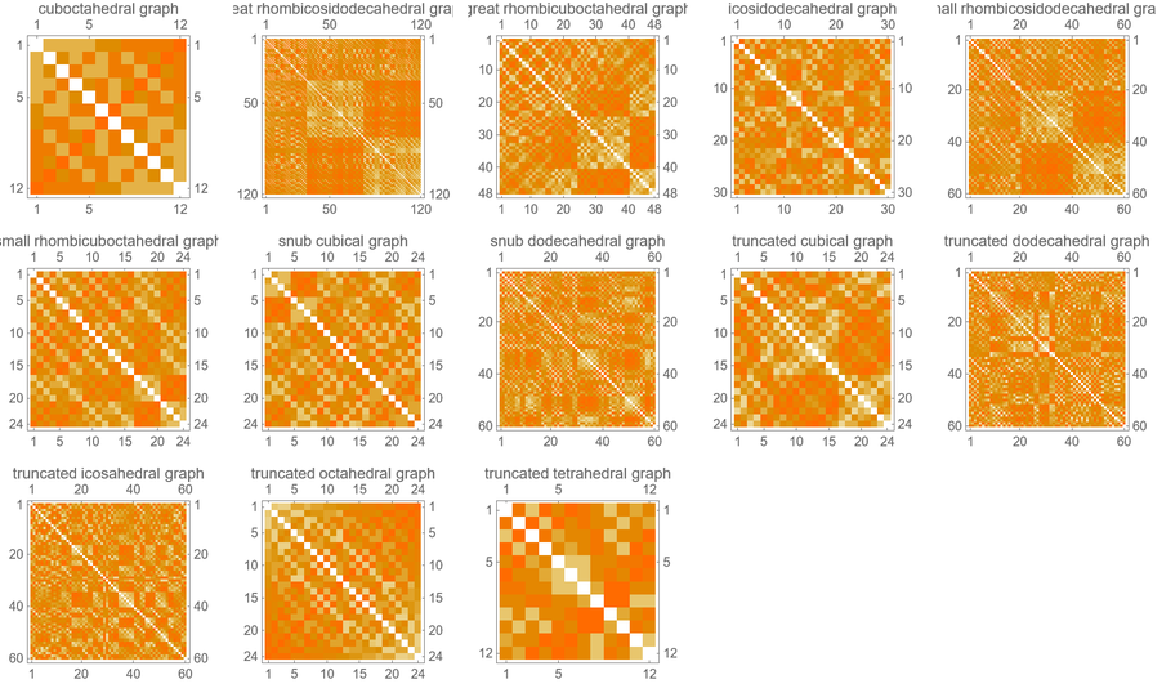 |
Rows and columns of the resistance matrix follow the order given by VertexList:
| In[13]:= |
| Out[13]= | 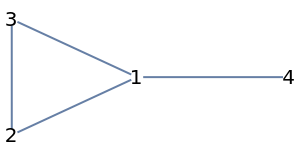 |
| In[14]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= |  |
The number of rows or columns of the resistance matrix is equal to the number of vertices:
| In[16]:= |
| Out[16]= | 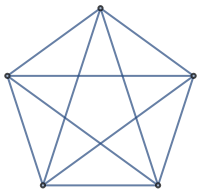 |
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
A pair of graphs with the same resistance spectra, due to Rickard:
| In[19]:= |
| Out[19]= | 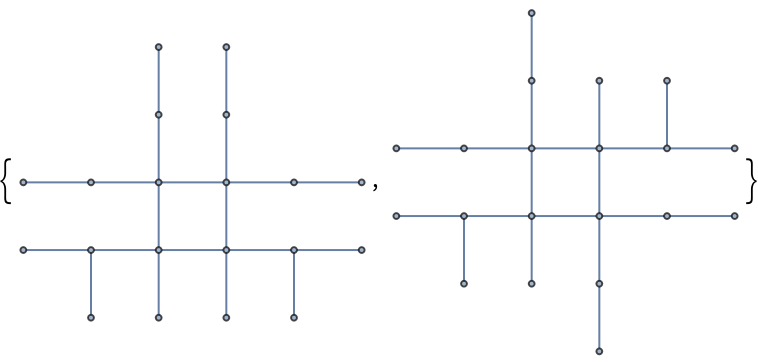 |
The two graphs are not isomorphic:
| In[20]:= |
| Out[20]= |
Compute their respective resistance spectra:
| In[21]:= | ![s1 = Sort[
DeleteCases[
Flatten[UpperTriangularize[
ResourceFunction["ResistanceMatrix"][g1], 1]], 0]];
s2 = Sort[
DeleteCases[
Flatten[UpperTriangularize[
ResourceFunction["ResistanceMatrix"][g2], 1]], 0]];](https://www.wolframcloud.com/obj/resourcesystem/images/6a3/6a3fc04f-e536-4cd0-a231-ef3c5923ae9f/22b5c4626e2dafe6.png) |
Check that they are identical:
| In[22]:= |
| Out[22]= |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License