Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RegularPolygonAngleRadius

Source Notebook

Compute the polar radius of a regular polygon

Contributed by: Erik Mahieu

ResourceFunction["RegularPolygonAngleRadius"][t,n]

computes the polar radius at angle t with respect to the x axis of a regular polygon with n vertices equally spaced around the unit circle.

ResourceFunction["RegularPolygonAngleRadius"][t,r,n]

computes the radius of a regular polygon whose vertices lie on a circle of radius r.

ResourceFunction["RegularPolygonAngleRadius"][t,t0,r,n]

starts at angle t0 with respect to the x axis.

Examples

Basic Examples (1) 

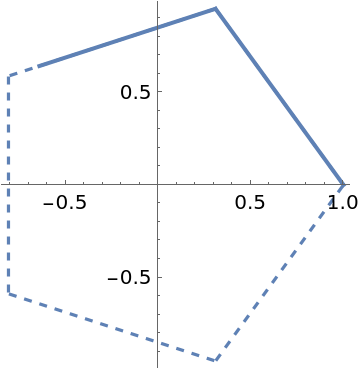
Draw the perimeter of a regular polygon using polar coordinates:

In[1]:=
With[{n = 5}, Show[MapThread[ PolarPlot[ ResourceFunction["RegularPolygonAngleRadius"][t, n], {t, 0, #1}, PlotStyle -> #2, ImageSize -> Small] &, {{3 \[Pi]/4, 2 \[Pi]}, {Thick, Dashed}}]]]
Out[1]=

Scope (2) 

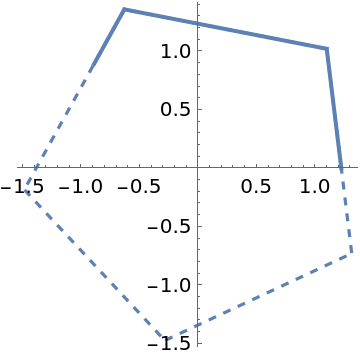
Use a different radius and starting angle:

In[2]:=
With[{n = 5, t0 = 0.75, r = 1.5}, Show[MapThread[ PolarPlot[ ResourceFunction["RegularPolygonAngleRadius"][t, t0, r, n], {t, 0, #1}, PlotStyle -> #2, ImageSize -> Small] &, {{3 \[Pi]/4, 2 \[Pi]}, {Thick, Dashed}}]]]
Out[2]=

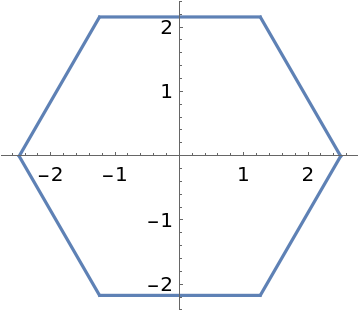
Draw the perimeter of any regular polygon using parametric coordinates:

In[3]:=
With[{n = 6, t0 = 0, r = 2.5}, ParametricPlot[ AngleVector[{ResourceFunction["RegularPolygonAngleRadius"][t, t0, r, n], t}], {t, 0, 2 \[Pi]}, ImageSize -> Small]]
Out[3]=

Applications (1) 

Construct a cylinder with a polygonal cross-section:

In[4]:=
ParametricPlot3D[ Insert[AngleVector[{ResourceFunction["RegularPolygonAngleRadius"][t, 0, 1, 5], t}], v, -1], {t, 0, 2 \[Pi]}, {v, -3, 3}, Axes -> False, Boxed -> False, Exclusions -> None, WorkingPrecision -> 20, PerformanceGoal -> "Quality", ImageSize -> Small]
Out[4]=

Properties and Relations (2) 

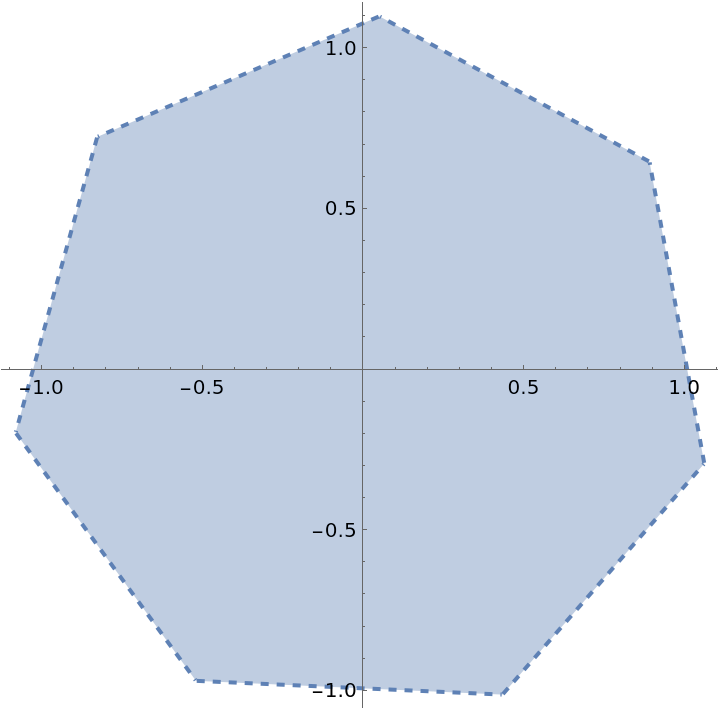
RegularPolygonAngleRadius gives the boundary of RegularPolygon:

In[5]:=
With[{t0 = \[Pi]/5, r = 1.1, n = 7}, PolarPlot[ ResourceFunction["RegularPolygonAngleRadius"][t, t0, r, n], {t, 0, 2 \[Pi]}, PlotStyle -> Directive[Dashed, Thick], Prolog -> {Directive[Opacity[0.4], ColorData[97, 1]], RegularPolygon[{r, t0}, n]}]]
Out[5]=

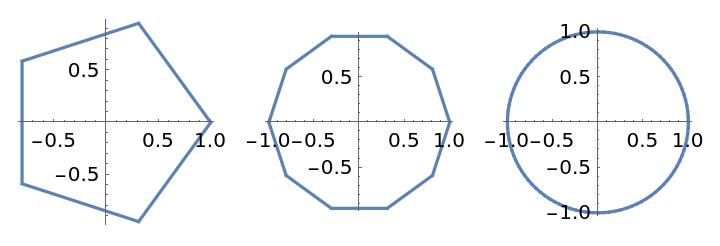
With n very large (>100), one gets an approximation to a circle:

In[6]:=
GraphicsRow[ PolarPlot[ ResourceFunction["RegularPolygonAngleRadius"][t, 0, 1, #], {t, 0, 2 \[Pi]}, ImageSize -> Small] & /@ {5, 10, 100}, ImageSize -> Medium]
Out[6]=

Neat Examples (2) 

Nested polygons:

In[7]:=
With[{p = 6}, Partition[ Table[PolarPlot[ Table[ResourceFunction["RegularPolygonAngleRadius"][ t, \[Pi]/n Mod[k, 2], Cos[\[Pi]/n]^k, n], {k, 0, p}] // Evaluate, {t, 0, 2 \[Pi]}, Axes -> None, PlotRange -> All, PlotStyle -> Directive[AbsoluteThickness[1.5], ColorData[97, 1]]], {n, 3, 8}], 3]] // GraphicsGrid
Out[7]=

Repeated circumscribed polygons:

In[8]:=
With[{n = 9}, PolarPlot[Flatten[Table[{\!\( \*UnderoverscriptBox[\(\[Product]\), \(j = 3\), \(k - 1\)]\(Sec[ \*FractionBox[\(\[Pi]\), \(j\)]]\)\), ResourceFunction["RegularPolygonAngleRadius"][t, 0, \!\( \*UnderoverscriptBox[\(\[Product]\), \(j = 3\), \(k\)]\(Sec[ \*FractionBox[\(\[Pi]\), \(j\)]]\)\), k]}, {k, 3, n}]] // Evaluate, {t, 0, 2 \[Pi]}, Axes -> None, PlotPoints -> 75, PlotRange -> All, PlotStyle -> Directive[AbsoluteThickness[1.5], ColorData[97, 1]]]]
Out[8]=

Publisher

Erik Mahieu

Version History

  • 1.0.0 – 30 November 2021

Related Resources

License Information