Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RegularHyperbolicTilingGraph

Source Notebook

Create a graph of a regular hyperbolic tiling

Contributed by: Wolfram Physics Project Team

ResourceFunction["RegularHyperbolicTilingGraph"][n,m,k]

generates a graph corresponding to a tiling of the hyperbolic plane where m regular n-gons share a vertex, propagated for k steps.

Details and Options

ResourceFunction["RegularHyperbolicTilingGraph"] gives an {n,m} regular hyperbolic tiling.
ResourceFunction["RegularHyperbolicTilingGraph"] is left unevaluated if the tiling specification is invalid.
ResourceFunction["RegularHyperbolicTilingGraph"] takes the same options as Graph.
Possible additional settings for the option GraphLayout include:
"Beltrami"embed graph on the Beltrami-Klein disk
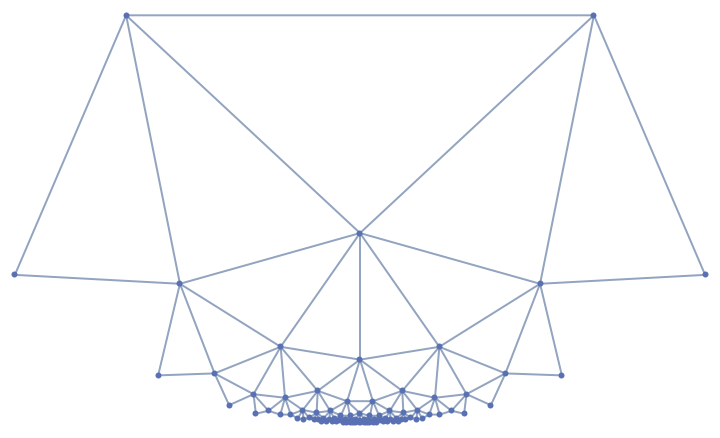
"HalfPlane"embed graph on the Poincaré half-plane
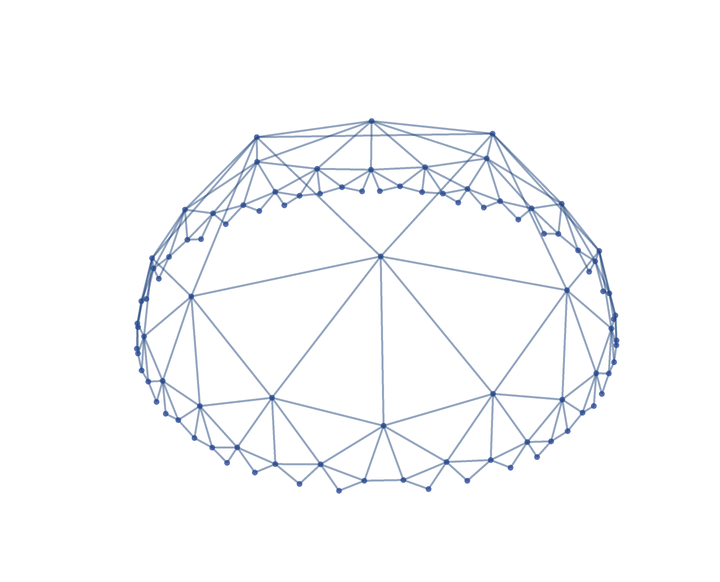
"Hemisphere"embed graph on a hemisphere (stereographic projection of Poincaré disk)
"Hyperboloid"embed graph in the hyperboloid (Minkowski) model
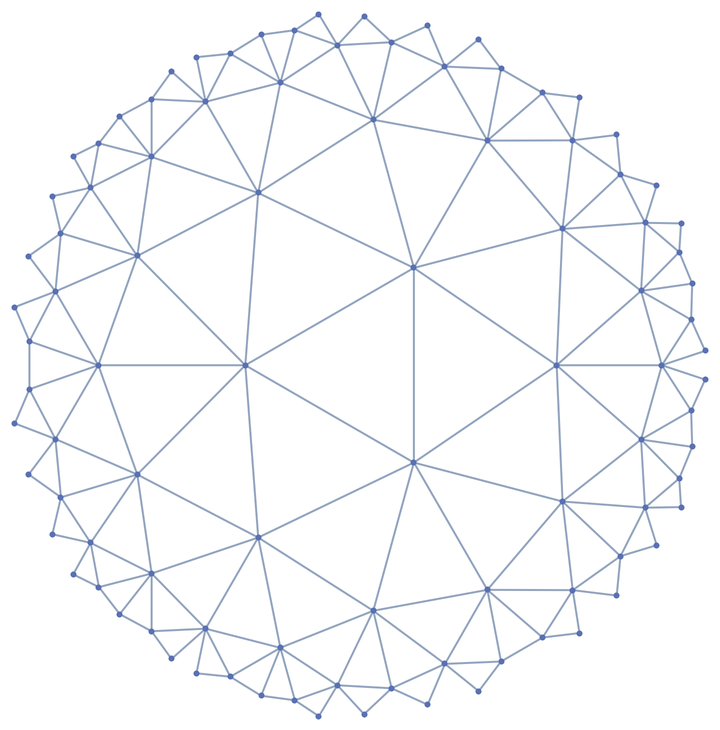
"Poincare"embed graph on the Poincaré disk

Examples

Basic Examples (2) 

Graph of a {5,4} regular hyperbolic tiling:

In[1]:=
ResourceFunction["RegularHyperbolicTilingGraph"][5, 4, 4]
Out[1]=

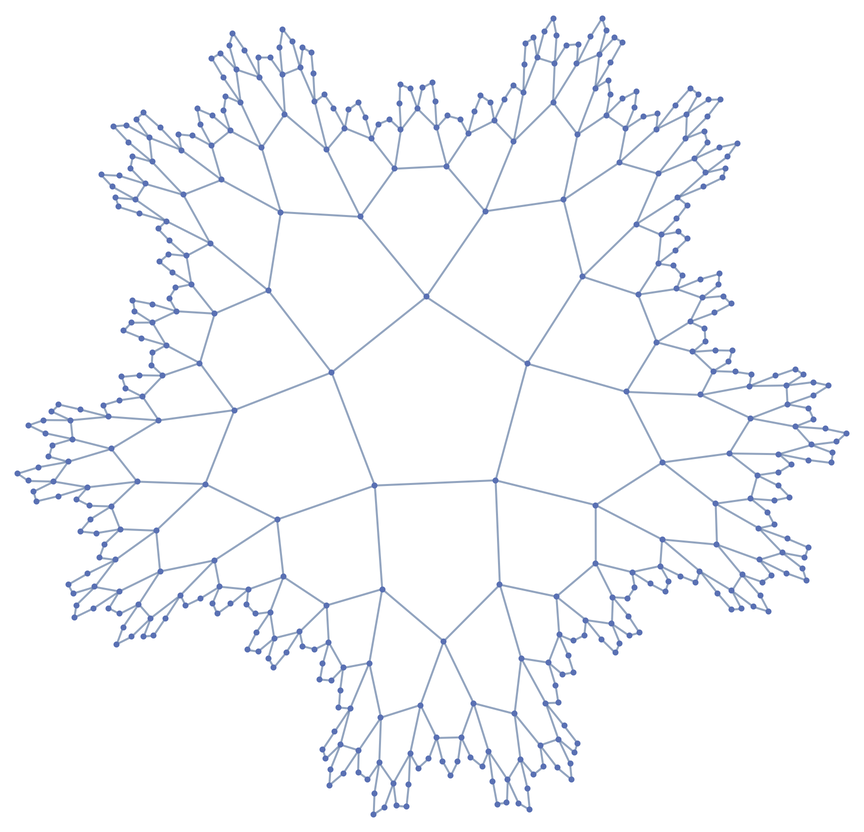
Show the graph in 3D:

In[2]:=
Graph3D[%, GraphLayout -> "SpringElectricalEmbedding"]
Out[2]=

Scope (1) 

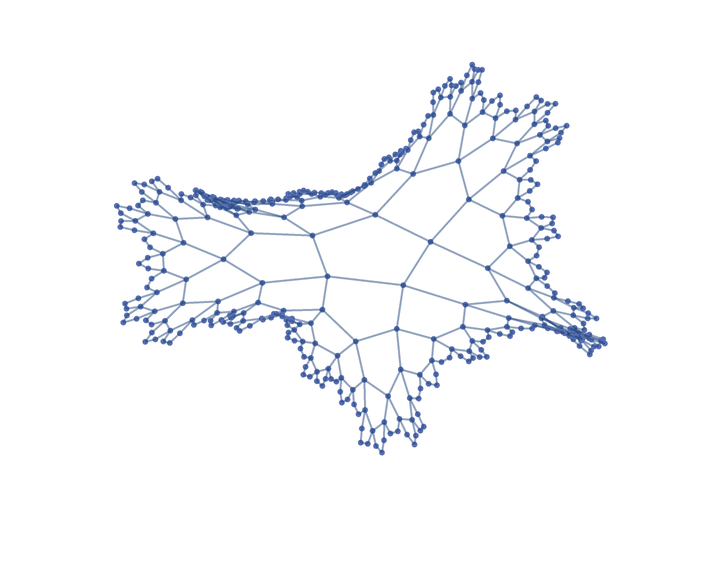
Show the steps in generating a {6,4} regular hyperbolic tiling, embedded on the Poincaré disk:

In[3]:=
Table[ResourceFunction["RegularHyperbolicTilingGraph"][6, 4, k, GraphLayout -> "Poincare", WorkingPrecision -> 20], {k, 4}]
Out[3]=

Options (6) 

GraphLayout (6) 

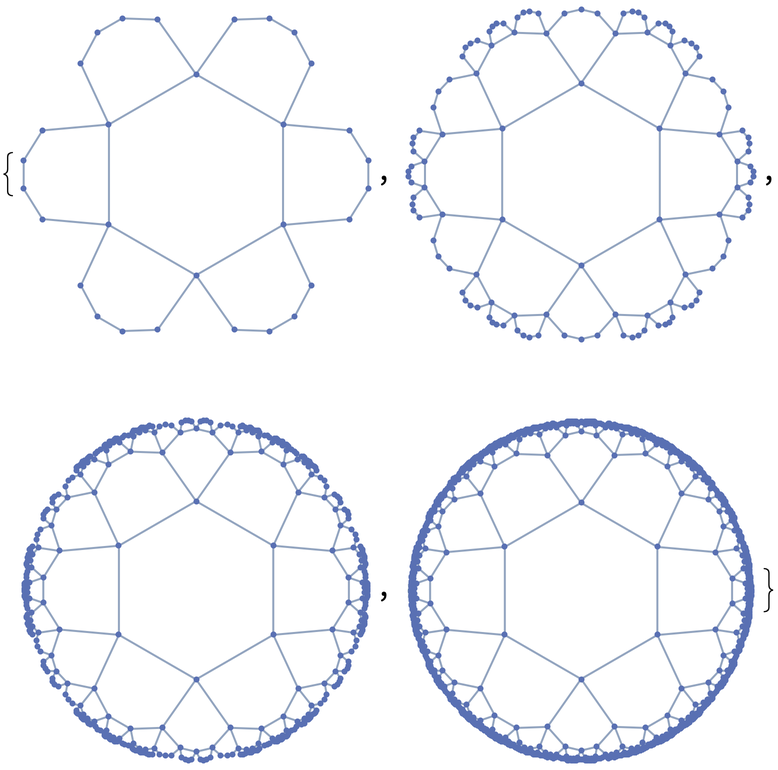
Embed the graph in the Beltrami-Klein disk:

In[4]:=
ResourceFunction["RegularHyperbolicTilingGraph"][3, 7, 6, GraphLayout -> "Beltrami"]
Out[4]=

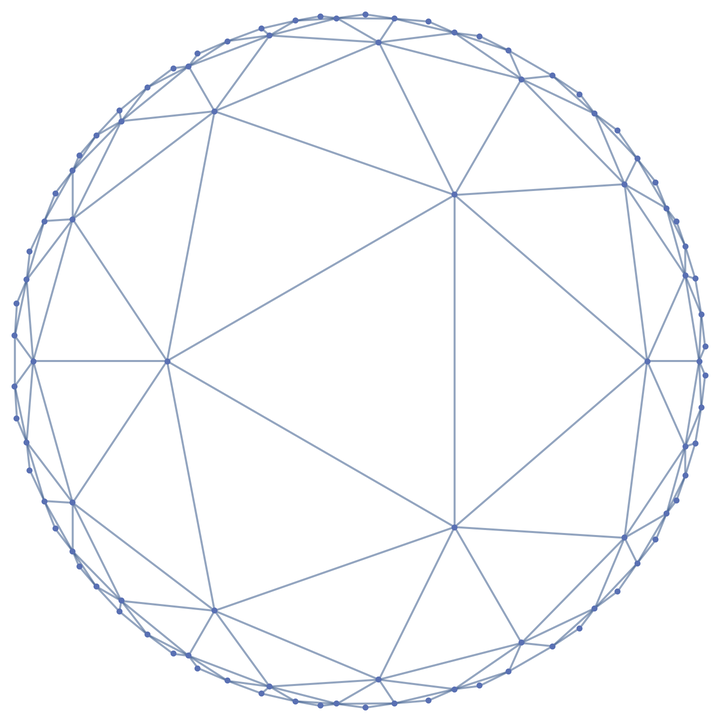
Embed the graph in the Poincaré disk:

In[5]:=
ResourceFunction["RegularHyperbolicTilingGraph"][3, 7, 6, GraphLayout -> "Poincare"]
Out[5]=

Embed the graph in the Poincaré half plane:

In[6]:=
ResourceFunction["RegularHyperbolicTilingGraph"][3, 7, 6, GraphLayout -> "HalfPlane"]
Out[6]=

Embed the graph in the hemisphere:

In[7]:=
ResourceFunction["RegularHyperbolicTilingGraph"][3, 7, 6, GraphLayout -> "Hemisphere"]
Out[7]=

Embed the graph in a hyperboloid:

In[8]:=
ResourceFunction["RegularHyperbolicTilingGraph"][3, 7, 6, GraphLayout -> "Hyperboloid"]
Out[8]=

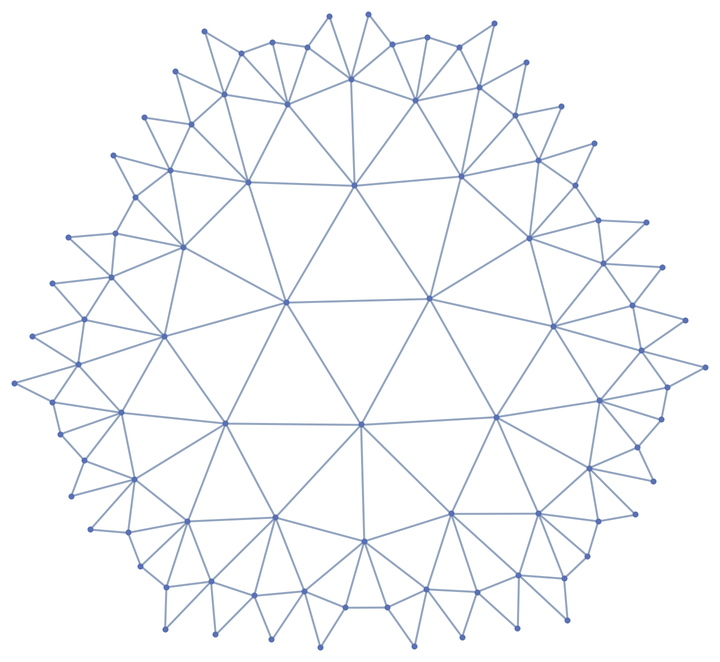
Use an embedding supported by Graph:

In[9]:=
ResourceFunction["RegularHyperbolicTilingGraph"][3, 7, 6, GraphLayout -> "SpringElectricalEmbedding"]
Out[9]=

Possible Issues (2) 

RegularHyperbolicTilingGraph returns unevaluated if the arguments do not correspond to a valid regular hyperbolic tiling:

In[10]:=
ResourceFunction["RegularHyperbolicTilingGraph"][5, 3, 4]
Out[10]=

For moderately sized arguments, generating the graph might take a long time:

In[11]:=
AbsoluteTiming[ ResourceFunction["RegularHyperbolicTilingGraph"][9, 7, 4]]
Out[11]=

Version History

  • 1.0.0 – 14 April 2020

Related Resources

License Information