Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RayTransferMatrix

Source Notebook

Calculate the ray transfer matrix of a Gaussian optical system

Contributed by: Julián Laverde

ResourceFunction["RayTransferMatrix"][{key1→val1,key2→val2,…}]

calculates the ABCD matrix of the optical system composed of the processes keyj with parameters valj.

Details

ResourceFunction["RayTransferMatrix"] returns the ABCD matrix (also known as the ray transfer matrix) of a cascaded system for performing ray tracing calculations under the paraxial approximation.
The available optical proccesses (keyj→valuej) are the following:
"Refraction"{r,n1,n2}refraction of a light ray on a spherical surface of radius r and refractive index n2 immersed in a medium of refractive index n1
"Reflection"{r}reflection of a light ray on a spherical surface of radius r
"Propagation"{d,n}propagation of a light ray a distance d in a medium of refractive index n
"ThinLens"{f}transmission through a thin lens of focal length f
"ThickLens"{r1,r2,n1,n2,t}transmission through a thick lens of first surface radius r1, second surface radius r2, refractive index n2 and center thickness t inmmersed in a medium of refractive index n1
"Prism"{k,d,n}transmission through a single prism of beam expansion factor k, path length d and refractive index n for orthogonal beam exit
The order of the optical components in the input list must be the one that light rays encounter.
The output ray {y2,θ2} is related to the input ray that crosses the input plane at a distance y1 from the optical axis, traveling in a direction that makes an angle θ1 with the optical axis given by Dot[ResourceFunction["RayTransferMatrix"][…], {y1,θ1}].
Use consistent length units for all parameters in all processes. The input ray vector units should also be consistent with the units used for the matrix.
For planar surfaces use Infinity as the radius.

Examples

Basic Examples (6) 

Calculate the refraction matrix:

In[1]:=
ResourceFunction[ "RayTransferMatrix"][{"Refraction" -> {R, Subscript[n, m], Subscript[ n, l]}}]
Out[1]=

Calculate the reflection matrix:

In[2]:=
ResourceFunction[ "RayTransferMatrix"][{"Reflection" -> {R}}] // MatrixForm
Out[2]=

Calculate the propagation matrix:

In[3]:=
ResourceFunction[ "RayTransferMatrix"][{"Propagation" -> {d, Subscript[n, m]}}] // MatrixForm
Out[3]=

Calculate the thin lens in a free-space matrix:

In[4]:=
ResourceFunction[ "RayTransferMatrix"][{"ThinLens" -> {Subscript[f, l]}}] // MatrixForm
Out[4]=

Calculate the thick lens matrix:

In[5]:=
ResourceFunction[ "RayTransferMatrix"][{"ThickLens" -> {Subscript[R, 1], Subscript[R, 2], Subscript[n, m], Subscript[n, l], Subscript[t, l]}}] // MatrixForm
Out[5]=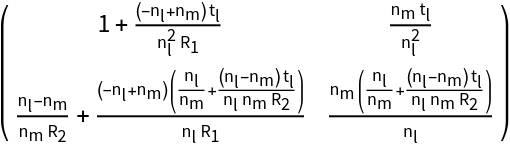

Calculate the single prism matrix:

In[6]:=
ResourceFunction[ "RayTransferMatrix"][{"Prism" -> {Subscript[k, p], Subscript[d, p], Subscript[n, p]}}] // MatrixForm
Out[6]=

Scope (2) 

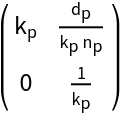Calculate the symbolic ray transfer matrix of a simple spherical lens by its processes:

In[7]:=
ResourceFunction[ "RayTransferMatrix"][{"Refraction" -> {Subscript[R, 1], Subscript[n, m], Subscript[n, l]}, "Propagation" -> {Subscript[t, l], Subscript[n, l]}, "Refraction" -> {Subscript[R, 2], Subscript[n, l], Subscript[n, m]}}] // MatrixForm
Out[7]=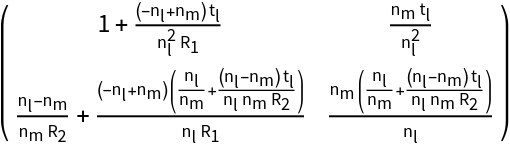

Calculate the system matrix of a plano-concave lens of 1 cm thickness:

In[8]:=
ResourceFunction[ "RayTransferMatrix"][{"Refraction" -> {-20, 1, 1.5}, "Propagation" -> {1, 1.5}, "Refraction" -> {\[Infinity], 1.5, 1}}]
Out[8]=

Applications (2) 

Calculate the system matrix of a Tessar lens:

In[9]:=
ResourceFunction[ "RayTransferMatrix"][{"Refraction" -> {1.628, 1, 1.6116}, "Propagation" -> {0.357, 1.6116}, "Refraction" -> {-27.57, 1.6116, 1}, "Propagation" -> {0.189, 1}, "Refraction" -> {-3.457, 1, 1.6053}, "Propagation" -> {0.081, 1.6053}, "Refraction" -> {1.582, 1.6053, 1}, "Propagation" -> {0.325, 1}, "Refraction" -> {\[Infinity], 1, 1.5123}, "Propagation" -> {0.217, 1.5123}, "Refraction" -> {1.920, 1.5123, 1.6116}, "Propagation" -> {0.396, 1.6116}, "Refraction" -> {-2.400, 1.6116, 1}}] // MatrixForm
Out[9]=

Calculate the height and angle at which a ray emerges coming toward the lens at a height of 2 cm above the optical axis and an angle of 5.73°:

In[10]:=
% . {2, 5.73 Degree}
Out[10]=

Calculate the system matrix of a planar optical cavity:

In[11]:=
ResourceFunction[ "RayTransferMatrix"][{"Propagation" -> {d, 1}, "Reflection" -> {\[Infinity]}, "Propagation" -> {-d, 1}, "Reflection" -> {\[Infinity]}}] // MatrixForm
Out[11]=

Possible Issues (1) 

Make sure that the list of values for each optical process has the required length:

In[12]:=
ResourceFunction["RayTransferMatrix"][{"Propagation" -> {d}}]
Out[12]=

Publisher

WolframSpecialProjects

Version History

  • 1.0.0 – 21 September 2021

Source Metadata

  • Citation:
    • Bahaa E. A. Saleh and Malvin Carl Teich (1991). Fundamentals of Photonics. New York: John Wiley & Sons. Section 1.4, pp. 26–36.
    • Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. §5.2.3. ISBN 0-201-11609-X.
    • K. Halbach, "Matrix Representation of Gaussian Optics", Am. J. Phys. 32, 90 (1964). DOI: 10.1119/1.1970159

Related Resources

License Information