Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RandomPolyhedralNet

Source Notebook

Create an unfolding net for a given polyhedron

Contributed by: Izidor Hafner and Ed Pegg Jr

ResourceFunction["RandomPolyhedralNet"][poly]

creates an unfolding net from a simple polyhedron poly.

ResourceFunction["RandomPolyhedralNet"][v,f]

creates an unfolding net from a polyhedron defined by vertices v and face indices f.

Details

A net of a polyhedron is a 2D representation that can be folded into a 3D polyhedron.
In ResourceFunction["RandomPolyhedralNet"][poly], poly can be any object that can be converted to a Polyhedron or a "Polyhedron" entity.
The output is a nested list of coordinate pairs defining the vertices of polygons.

Examples

Basic Examples (2) 

Create a random net for a cube:

In[1]:=
flat = ResourceFunction["RandomPolyhedralNet"][Cube[]]
Out[1]=

Show the random net:

In[2]:=
Graphics[Map[Line, flat], ImageSize -> Small]
Out[2]=

Scope (3) 

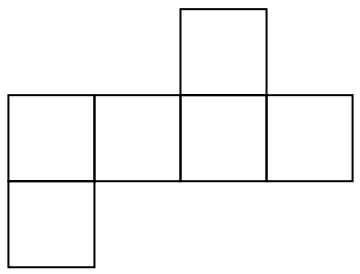Construct a random net for a cube represented through a list of vertices and face indices:

In[3]:=
cubevertices = {{-1, -1, -1}, {-1, -1, 1}, {-1, 1, -1}, {-1, 1, 1}, {1, -1, -1}, {1, -1, 1}, {1, 1, -1}, {1, 1, 1}}; cubefaces = {{1, 3, 7, 5}, {2, 1, 5, 6}, {4, 3, 1, 2}, {8, 4, 2, 6}, {8, 6, 5, 7}, {8, 7, 3, 4}}; flat = ResourceFunction["RandomPolyhedralNet"][cubevertices, cubefaces]
Out[5]=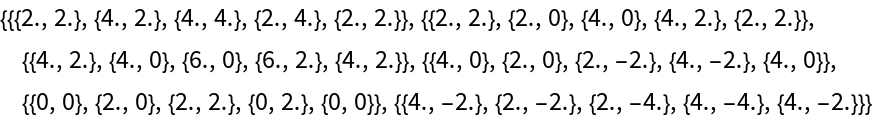

Show the random net:

In[6]:=
Graphics[Map[Line, flat], ImageSize -> Small]
Out[6]=

Make a random net for the gyrobifastigium:

In[7]:=
flat = ResourceFunction["RandomPolyhedralNet"][ Entity["Polyhedron", "Gyrobifastigium"]]
Out[7]=

Show the random net:

In[8]:=
Graphics[Map[Line, flat], ImageSize -> Small]
Out[8]=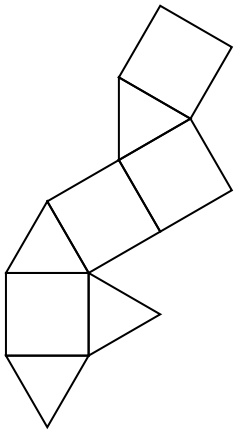

A randomly-generated convex hull polyhedron:

In[9]:=
poly = RandomPolyhedron[{"ConvexHull", 8}]
Out[9]=

Generate and show a random net:

In[10]:=
flat = ResourceFunction["RandomPolyhedralNet"][poly]; Graphics[Map[Line, flat], ImageSize -> Small]
Out[11]=

Properties and Relations (1) 

Use SeedRandom for reproducibility:

In[12]:=
BlockRandom[SeedRandom[14344]; flat = ResourceFunction["RandomPolyhedralNet"][Icosahedron[]]; Graphics[Map[Line, flat], ImageSize -> Small]]
Out[12]=

Possible Issues (3) 

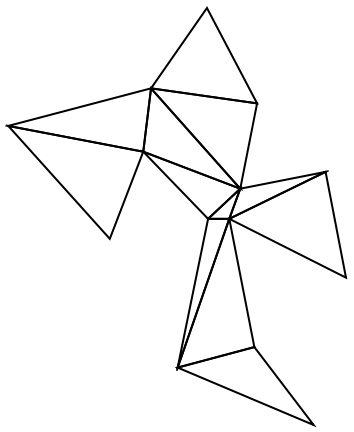RandomPolyhedralNet only works for simple polyhedra:

In[13]:=
poly = Polyhedron[{{0, 0, 0}, {0, 3, 0}, {3, 3, 0}, {3, 0, 0}, {0, 0, 3}, {0, 3, 3}, {3, 3, 3}, {3, 0, 3}, {1, 1, 1}, {1, 2, 1}, {2, 2, 1}, {2, 1, 1}, {1, 1, 2}, {1, 2, 2}, {2, 2, 2}, {2, 1, 2}}, {{2, 3, 4, 1}, {1, 4, 8, 5}, {4, 3, 7, 8}, {3, 2, 6, 7}, {2, 1, 5, 6}, {5, 8, 7, 6}} -> {{{10, 11, 12, 9}, {9, 12, 16, 13}, { 12, 11, 15, 16}, {11, 10, 14, 15}, {10, 9, 13, 14}, {13, 16, 15, 14}}}]; ResourceFunction["RandomPolyhedralNet"][poly]
Out[14]=
In[15]:=
SimplePolyhedronQ[poly]
Out[15]=

Concave polyhedra often have overlapping random nets:

In[16]:=
flat = ResourceFunction["RandomPolyhedralNet"][ PolyhedronData["RhombicHexecontahedron", "Polyhedron"]]; Graphics[Map[Line, flat], ImageSize -> Small]
Out[17]=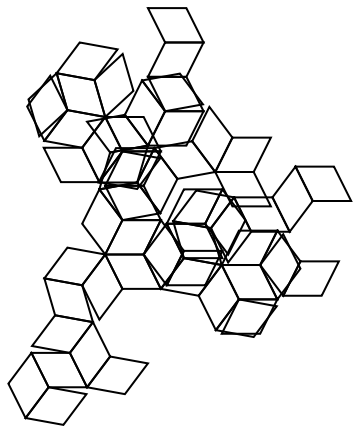

Verify that the rhombic hexecontahedron is not convex:

In[18]:=
ConvexPolyhedronQ[ PolyhedronData["RhombicHexecontahedron", "Polyhedron"]]
Out[18]=

It may not be clear how a net folds together:

In[19]:=
flat = ResourceFunction["RandomPolyhedralNet"][ PolyhedronData["SnubDisphenoid", "Polyhedron"]]; Graphics[Map[Line, flat], ImageSize -> Small]
Out[20]=

Neat Examples (2) 

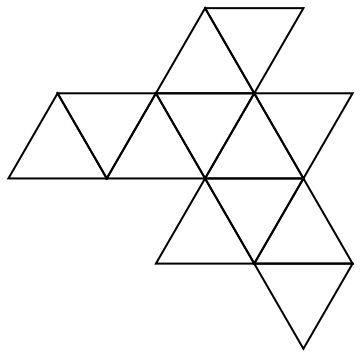Find a random net for the hexakis icosahedron:

In[21]:=
flat = ResourceFunction["RandomPolyhedralNet"][ PolyhedronData["HexakisIcosahedron", "Polyhedron"]]; Graphics[Map[Line, flat], ImageSize -> Small]
Out[22]=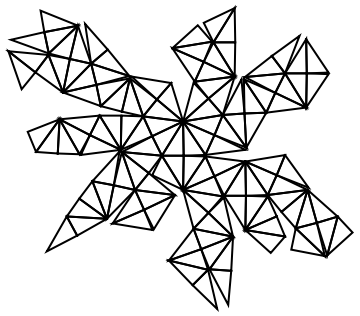

Find a random net for the great rhombicosidodecahedron:

In[23]:=
flat = ResourceFunction["RandomPolyhedralNet"][ PolyhedronData["GreatRhombicosidodecahedron", "Polyhedron"]]; Graphics[Map[Line, flat], ImageSize -> Small]
Out[15]=

Requirements

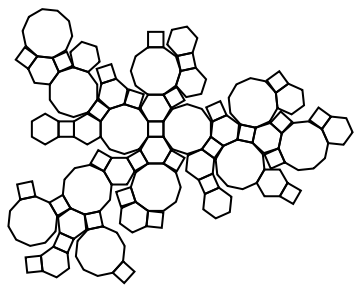Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 08 November 2023

Related Resources

License Information