Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RandomCA

Source Notebook

Randomly sample different cellular automaton rule spaces

Contributed by: Bradley Klee

ResourceFunction["RandomCA"][{k}]

gives pseudorandomly chosen defining data for a k-colored, nearest-neighbor CellularAutomaton in one dimension.

ResourceFunction["RandomCA"][{k,r}]

gives pseudorandomly chosen defining data for a k-colored, r-ranged CellularAutomaton in one dimension.

Details

ResourceFunction["RandomCA"] takes two options: "Quiescent" and "Type".
When "Quiescent" is set to True, input blocks of all zeros must output to zero. Setting "Quiescent" to a list of integers {x1, x2,…} forces input blocks of all xi to output to a single xi, i.e. sets the rule {xi, xi,…, xi} ↦ xi.
When "Type" is set to "Symmetric", "Totalistic", "OuterTotalistic", "Multiset" or "OuterMultiset", the defining data is chosen from the corresponding subset of the full {k, r} rule space.
"Totalistic" and "OuterTotalistic" are as described in the CellularAutomaton reference page.
For "Symmetric", whenever two inputs are equivalent by a space-like reflection, so too must their outputs be equivalent by space-like reflection.
The "Multiset" subspace identifies input blocks of length 2r+1 as if they were multisets, i.e. the update rule ignores the order in which values appear in an input block. That is, when lists x and y satisfy Length[x]=Length[y]=2r+1 and Sort[x]=Sort[y]=z, this means that CellularAutomaton[data][x] =CellularAutomaton[data][y]=CellularAutomaton[data][z]={c,c,…,c}, where c is a valid color integer.
The "OuterMultiset" subspace is to "Multiset" as "OuterTotalistic" is to "Totalistic". To construct the canonical signature of an input block, the central cell is kept separate, while 2r values remaining to left and right are listed in some chosen order, typically ascending. When two blocks have the same signature, they also have the same output.

Examples

Basic Examples (3) 

Choose a random elementary CA rule:

In[1]:=
SeedRandom[123]; rule = ResourceFunction["RandomCA"][{2}]
Out[2]=

Plot the rule with a random initial condition over a few steps:

In[3]:=
ArrayPlot[CellularAutomaton[rule, RandomInteger[1, 50], 50], PixelConstrained -> 4, Frame -> False]
Out[3]=

Show the RulePlot for a randomly chosen rule with a larger r=2 neighborhood:

In[4]:=
SeedRandom[1234]; RulePlot[CellularAutomaton[ResourceFunction["RandomCA"][{2, 2}]]]
Out[5]=

Plot the evolution of a 4-color CA:

In[6]:=
SeedRandom[123]; ArrayPlot[ CellularAutomaton[ResourceFunction["RandomCA"][{4}], RandomInteger[3, 50], 50], ColorRules -> {0 -> Red, 1 -> Green, 2 -> Blue, 3 -> Yellow}, PixelConstrained -> 4, Frame -> False]
Out[7]=

Scope (2) 

Rule spaces can be arbitrarily large:

In[8]:=
ResourceFunction["RandomCA"][{10}]
Out[8]=

Choose a random multiset cellular automaton:

In[9]:=
SeedRandom[3245]; mcode = ResourceFunction["RandomCA"][{3}, "Type" -> "Multiset", "Quiescent" -> {0, 1, 2}]
Out[10]=

Plot a random evolution:

In[11]:=
ArrayPlot[CellularAutomaton[mcode, RandomInteger[2, 50], 50], PixelConstrained -> 4]
Out[11]=

Check whether the rule is also totalistic:

In[12]:=
AllTrue[Map[CellularAutomaton[mcode], GatherBy[Tuples[Range[0, 2], 3], Total], {2}], SameQ @@ # &]
Out[12]=

Options (6) 

Quiescent (3) 

Choose a totally quiescent 3-color cellular automaton:

In[13]:=
SeedRandom[123]; code = ResourceFunction["RandomCA"][{3}, "Quiescent" -> {0, 1, 2}]
Out[14]=

Check the quiescence property using RulePlot:

In[15]:=
RulePlot[CellularAutomaton[code]]
Out[15]=

Compare with a zero-only quiescent code:

In[16]:=
SeedRandom[123]; RulePlot[ CellularAutomaton[ ResourceFunction["RandomCA"][{3}, "Quiescent" -> True]]]
Out[17]=

Type (3) 

Choose a random totalistic cellular automaton:

In[18]:=
SeedRandom[123]; code = ResourceFunction["RandomCA"][{2}, "Type" -> "Totalistic"]
Out[19]=

Plot the evolution with a random initial condition:

In[20]:=
ArrayPlot[CellularAutomaton[code, RandomInteger[1, 50], 10], PixelConstrained -> 4, Frame -> False]
Out[20]=

Choose a random multiset cellular automaton:

In[21]:=
SeedRandom[1234]; code = ResourceFunction["RandomCA"][{3}, "Type" -> "Multiset"]
Out[22]=

Plot the evolution with a random initial condition:

In[23]:=
ArrayPlot[CellularAutomaton[code, RandomInteger[1, 50], 10], PixelConstrained -> 4, Frame -> False]
Out[23]=

Choose a reflection-symmetric 2-color cellular automaton:

In[24]:=
SeedRandom[123]; code = ResourceFunction["RandomCA"][{2}, "Type" -> "Symmetric"]
Out[25]=

Inspect for the symmetric property using RulePlot:

In[26]:=
RulePlot[CellularAutomaton[code]]
Out[26]=

Properties and Relations (2) 

Check the "Quiescent" property:

In[27]:=
With[{code = ResourceFunction["RandomCA"][{3}, "Quiescent" -> {0, 1, 2}]}, AllTrue[{0, 1, 2}, MatchQ[CellularAutomaton[code][Table[#, 10]], Table[#, 10]] &]]
Out[27]=

Check the "Multiset" property:

In[28]:=
With[{code = ResourceFunction["RandomCA"][{3}, "Type" -> "Multiset", "Quiescent" -> {0, 1, 2}]}, AllTrue[Map[CellularAutomaton[code], GatherBy[Tuples[Range[0, 2], 3], Sort], {2}], SameQ @@ # &]]
Out[28]=

Neat Examples (2) 

Generate multiset cellular automaton rules that are not totalistic:

In[29]:=
rules = Module[{dom, rule, rules}, SeedRandom[3210]; dom = GatherBy[Tuples[Range[0, 2], 3], Total]; Table[Until[ AllTrue[Map[CellularAutomaton[rule], dom, {2}], SameQ @@ # &], rule = ResourceFunction["RandomCA"][{3}, "Type" -> "Multiset"]]; rule, {i, 16}]]
Out[29]=

Visualize these cellular automata:

In[30]:=
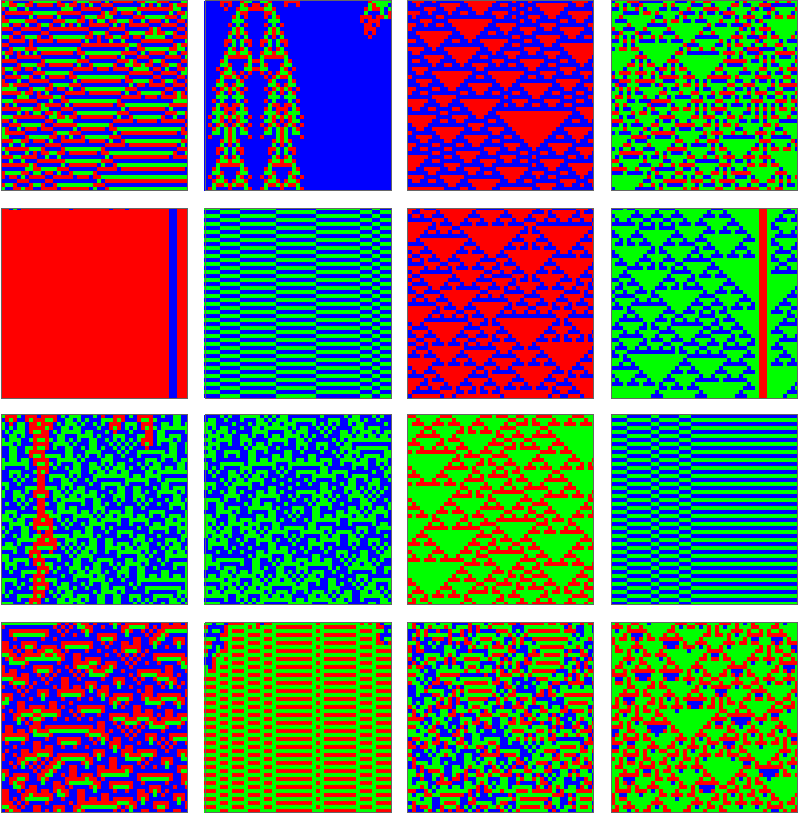
GraphicsGrid[Partition[ArrayPlot[ CellularAutomaton[#, RandomInteger[2, 50], 50], ColorRules -> {0 -> Red, 1 -> Green, 2 -> Blue}, PixelConstrained -> 2] & /@ rules, 4]]
Out[30]=

Publisher

Brad Klee

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 20 December 2023

Related Resources

License Information