Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RadicalInverse

Source Notebook

Compute the radical inverse of an integer to a given base

Contributed by: Jan Mangaldan

ResourceFunction["RadicalInverse"][n]

gives the base 10 radical inverse of the integer n.

ResourceFunction["RadicalInverse"][b,n]

gives the base-b radical inverse of the integer n.

Details

The radical inverse is also known as the van der Corput sequence.
Integer mathematical function, suitable for both symbolic and numerical manipulation.
The base-b radical inverse of n is defined as , where is the base-b expansion of n, and m is IntegerLength[n,b].
The radical inverse is usually used for computing Halton and Hammersley low-discrepancy sequences for quasi-Monte Carlo methods.

Examples

Basic Examples (3) 

The base-10 radical inverse of 42:

In[1]:=
ResourceFunction["RadicalInverse"][42]
Out[1]=

The base-2 radical inverse of 42:

In[2]:=
ResourceFunction["RadicalInverse"][2, 42]
Out[2]=

Plot the binary radical inverse:

In[3]:=
DiscretePlot[ResourceFunction["RadicalInverse"][2, n], {n, 0, 100}]
Out[3]=

Scope (2) 

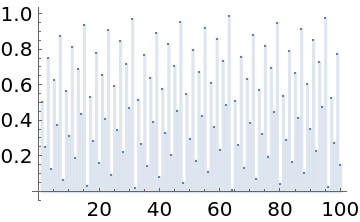Evaluate for large arguments:

In[4]:=
ResourceFunction["RadicalInverse"][50!]
Out[4]=

RadicalInverse automatically threads over lists:

In[5]:=
ResourceFunction["RadicalInverse"][2, {31, 32, 33}]
Out[5]=

Applications (4) 

Demonstrate the filling of the unit interval with the decimal radical inverse, also known as the van der Corput sequence:

In[6]:=
NumberLinePlot[ResourceFunction["RadicalInverse"][10, Range[100]]]
Out[6]=

Generate a 2D Halton sequence with bases 2 and 3:

In[7]:=
ListPlot[Table[ ResourceFunction["RadicalInverse"][{2, 3}, k], {k, 256}], AspectRatio -> Automatic, PlotRange -> {{0, 1}, {0, 1}}]
Out[7]=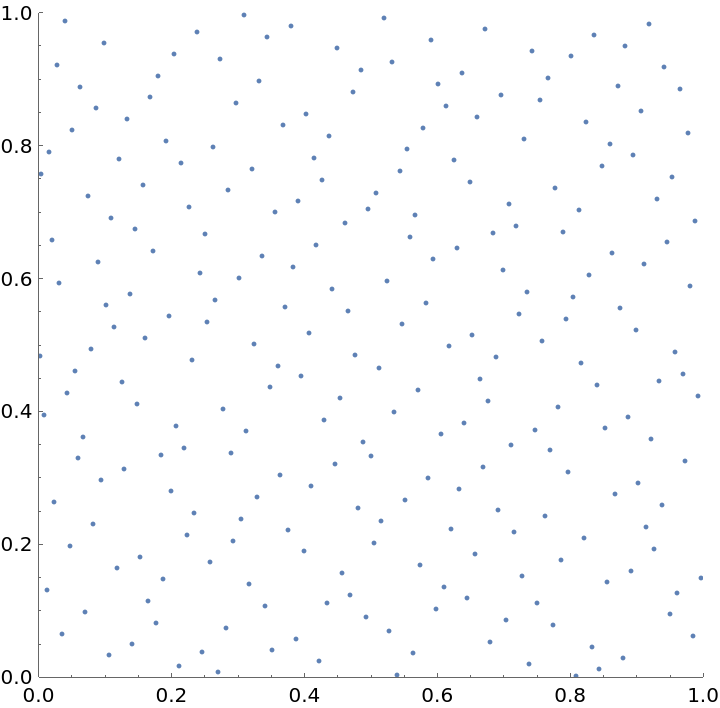

Generate a 2D binary Hammersley sequence:

In[8]:=
With[{n = 256}, ListPlot[Table[{k/n, ResourceFunction["RadicalInverse"][2, k]}, {k, n}], AspectRatio -> Automatic, PlotRange -> {{0, 1}, {0, 1}}]]
Out[8]=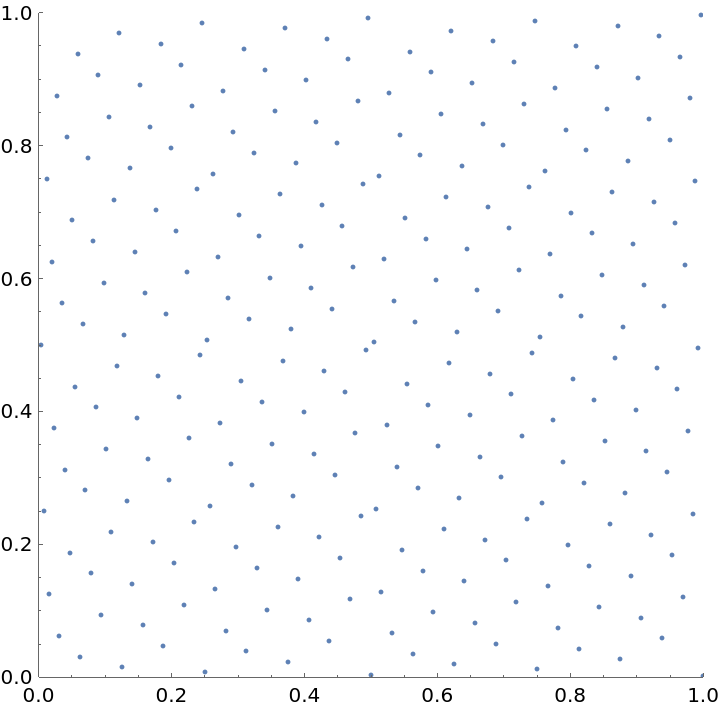

Compare the Halton and Hammersley sequences for approximating π by quasi-Monte Carlo integration:

In[9]:=
With[{n = 2^13}, N[4 Mean[Boole[# . # <= 1] & /@ Table[ResourceFunction["RadicalInverse"][{2, 3}, k], {k, n}]]]]
Out[9]=
In[10]:=
With[{n = 2^13}, N[4 Mean[Boole[# . # <= 1] & /@ Table[{k/n, ResourceFunction["RadicalInverse"][2, k]}, {k, n}]]]]
Out[10]=

Version History

  • 1.0.0 – 07 June 2021

Source Metadata

  • Citation:
    • Halton J.H., "On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals." Numerische Mathematik, vol. 2, 84–90, 1960. DOI: 10.1007/BF01386213
    • Hammersley J.M., "Monte Carlo methods for solving multivariable problems." Annals of the New York Academy of Sciences, vol. 86, 844–874, 1960. DOI: 10.1111/j.1749-6632.1960.tb42846.x
    • van der Corput J.G., "Verteilungsfunktionen I & II." Proceedings of the Koninklijke Akademie van Wetenschappen Te Amsterdam, vol. 38, 813–821 & 1058-1066, 1935. https://www.dwc.knaw.nl/DL/publications/PU00014607.pdf

Related Resources

License Information