Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Decompose a graphics 3D primitive into polygons when possible
ResourceFunction["PrimitiveToPolygons"][pr] decomposes the graphics 3D primitive pr into polygons when possible. |
A Parallelepiped object is converted to polygons:
| In[1]:= |
| Out[1]= | 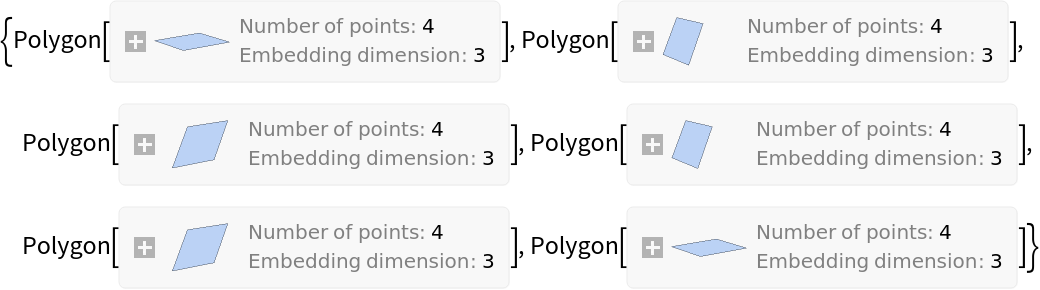 |
Display as tubes:
| In[2]:= |
| Out[2]= | 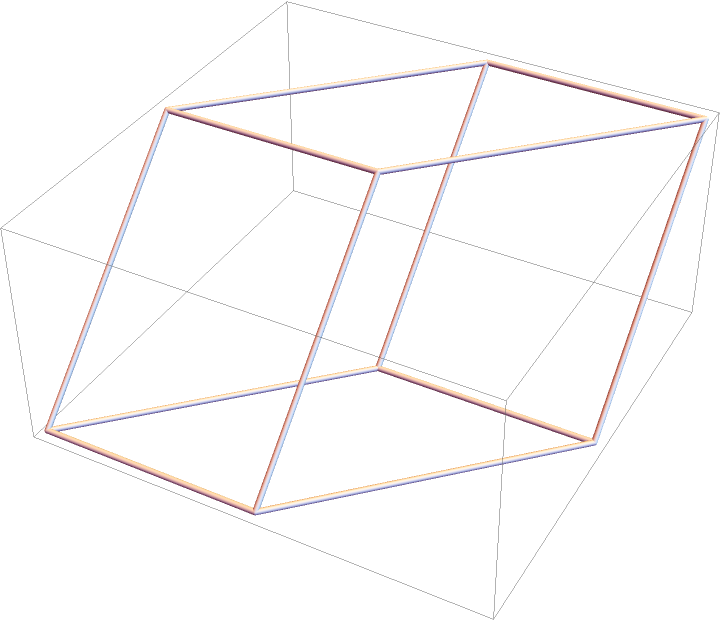 |
Using VertexTextureCoordinates:
| In[3]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/f4020b13-642a-40c3-99c9-ba90f2f322e4"]](https://www.wolframcloud.com/obj/resourcesystem/images/723/72323c97-e205-4b3d-9599-6f07f14455ba/5ec74a2db8550914.png) |
| Out[3]= |  |
Number of polygons:
| In[4]:= |
| Out[4]= |
A tetrahedron with edge length 2:
| In[5]:= |
| Out[5]= |  |
Using VertexColors:
| In[6]:= |
| Out[6]= | 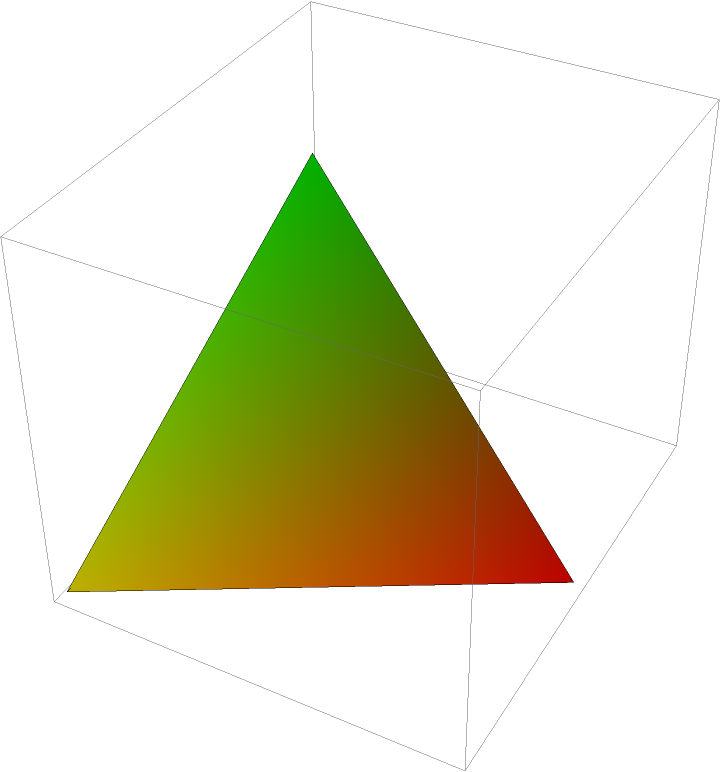 |
A pyramid:
| In[7]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/da784fff-cf99-46c1-8731-9a3d52daed51"]](https://www.wolframcloud.com/obj/resourcesystem/images/723/72323c97-e205-4b3d-9599-6f07f14455ba/595c64eed1ac94e2.png) |
| Out[7]= | 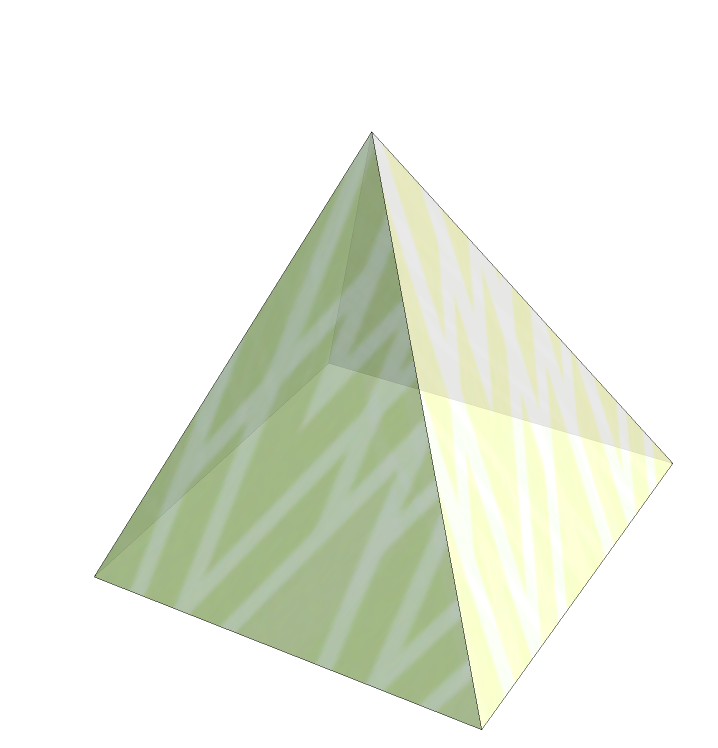 |
A simplex in dimension 3 with texture:
| In[8]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/775d9262-7c28-4d40-9b7b-184f95f211ed"]](https://www.wolframcloud.com/obj/resourcesystem/images/723/72323c97-e205-4b3d-9599-6f07f14455ba/36a59ca3080cc556.png) |
| Out[8]= |  |
Other graphics primitives:
| In[9]:= | ![Graphics3D[
ResourceFunction["PrimitiveToPolygons"][#]] & /@ {Cylinder[], Sphere[], Ball[], SphericalShell[], Cone[], Ellipsoid[{0, 0, 0}, {4, 3, 2}], Tube[{{0, 0, 0}, {1, 1, 1}}, .2], CapsuleShape[]}](https://www.wolframcloud.com/obj/resourcesystem/images/723/72323c97-e205-4b3d-9599-6f07f14455ba/3f8af4e3fd5e79e8.png) |
| Out[9]= | 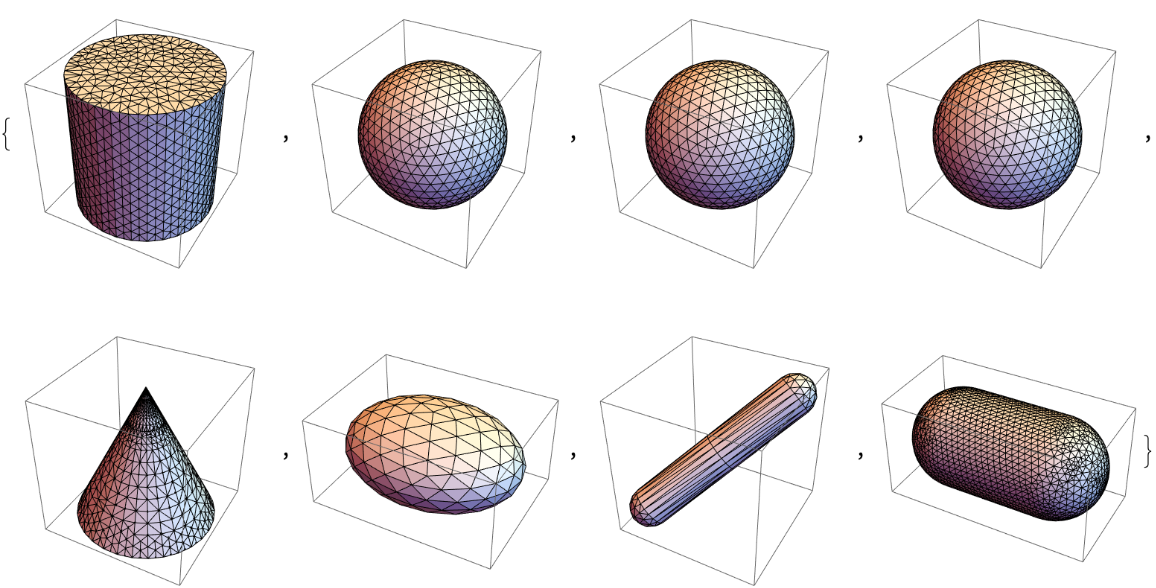 |
Using Polyhedron:
| In[10]:= |
| Out[10]= | 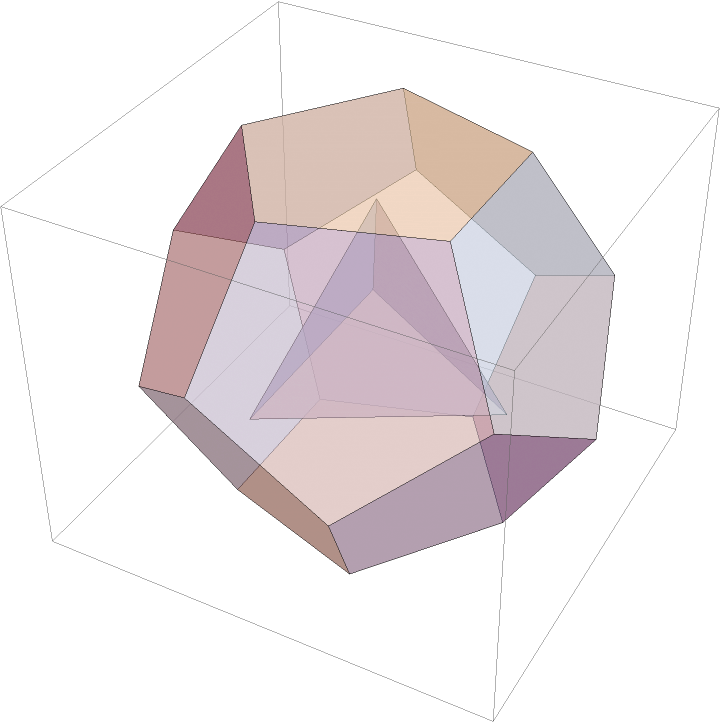 |
Using Polyhedron with VertexTextureCoordinates:
| In[11]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9162eaaf-405c-487e-a28f-8d9fb41368a3"]](https://www.wolframcloud.com/obj/resourcesystem/images/723/72323c97-e205-4b3d-9599-6f07f14455ba/1d5527751981b840.png) |
| Out[11]= | 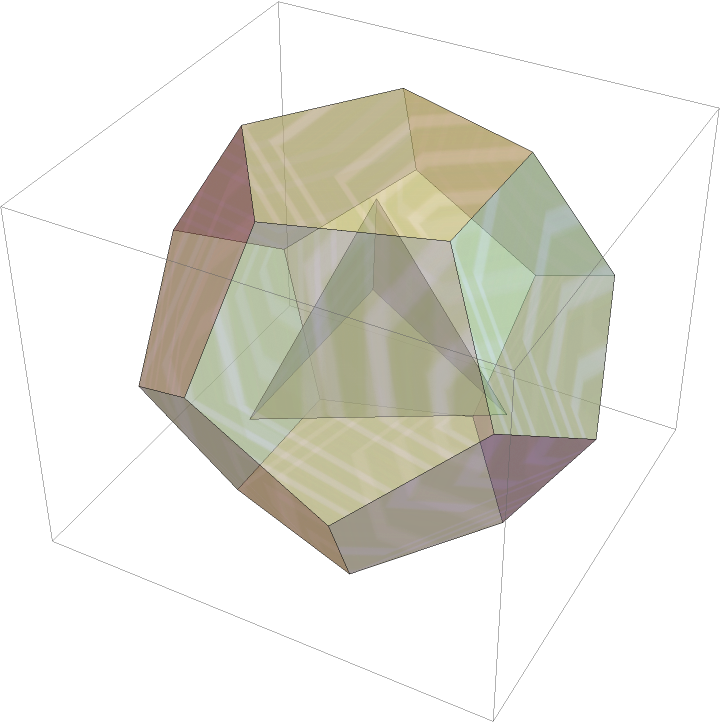 |
Scale and rotate polygons:
| In[12]:= |
| Out[12]= | 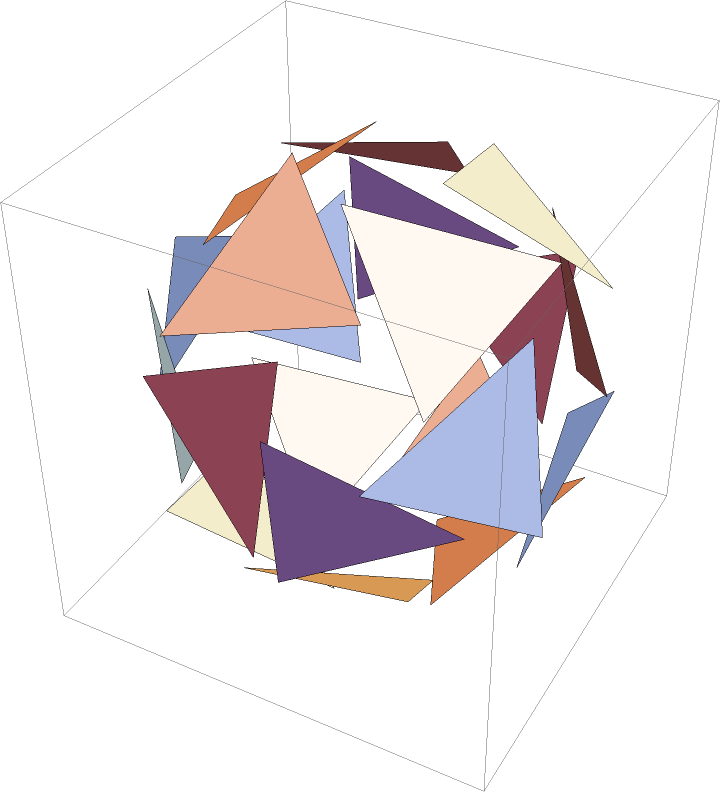 |
| In[13]:= |
| Out[13]= |  |
A Raster3D with gray levels:
| In[14]:= |
| Out[14]= |  |
A Raster3D with RGB colors:
| In[15]:= |
| Out[15]= |  |
The resource functions PerforatePolygons and OutlinePolygons internally use PrimitiveToPolygons:
| In[16]:= |
| Out[16]= |  |
| In[17]:= | ![Graphics3D@
ResourceFunction["PrimitiveToPolygons"][
Prism[{{1, 0, 1}, {0, 0, 0}, {2, 0, 0}, {1, 2, 1}, {0, 2, 0}, {2, 2, 0}}]] // ResourceFunction["OutlinePolygons"]](https://www.wolframcloud.com/obj/resourcesystem/images/723/72323c97-e205-4b3d-9599-6f07f14455ba/2b578324b0921ea6.png) |
| Out[17]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License