Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Outline polygons by beam-like representation
ResourceFunction["OutlinePolygons"][gr] outlines the polygons in the 3D graphics gr by beam-like representations. | |
ResourceFunction["OutlinePolygons"][gr, inner, outer] outlines the polygons with ratios inner and outer. |
An outlined tetrahedron:
| In[1]:= | ![ResourceFunction["OutlinePolygons"][
Graphics3D[
Polygon /@ {{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}, {{0, 1, 0}, {1, 0, 0}, {0, 0, 0}}, {{0, 0, 1}, {0, 0, 0}, {1, 0, 0}}, {{0, 0, 0}, {0, 0, 1}, {0, 1, 0}}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/2e0f38198029a8a1.png) |
| Out[1]= | 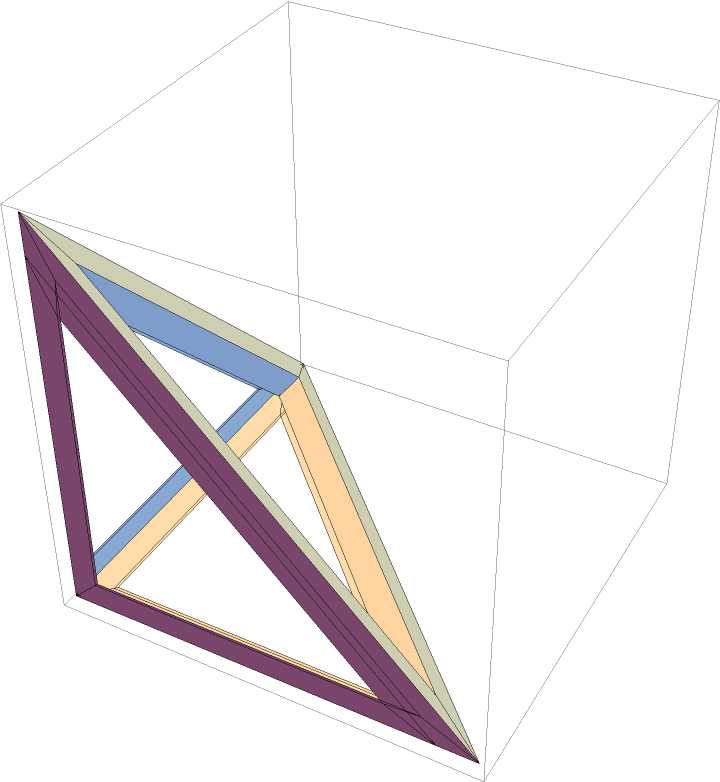 |
Specify the inner and outer ratios:
| In[2]:= | ![ResourceFunction["OutlinePolygons"][\!\(\*
Graphics3DBox[
{EdgeForm[None], Polygon3DBox[{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}], Polygon3DBox[{{0, 1, 0}, {1, 0, 0}, {0, 0, 0}}], Polygon3DBox[{{0, 0, 1}, {0, 0, 0}, {1, 0, 0}}], Polygon3DBox[{{0, 0, 0}, {0, 0, 1}, {0, 1, 0}}]},
ImageSize->{90., 90.},
ViewAngle->0.5011114127587019,
ViewPoint->{1.3, -2.4, 2.},
ViewVertical->{0., 0., 1.}]\), .5, .8]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/6b67b0bbfc0babde.png) |
| Out[2]= | 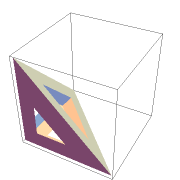 |
A spikey:
| In[3]:= |
| Out[3]= |  |
OutlinePolygons works with other primitives:
| In[4]:= |
| Out[4]= | 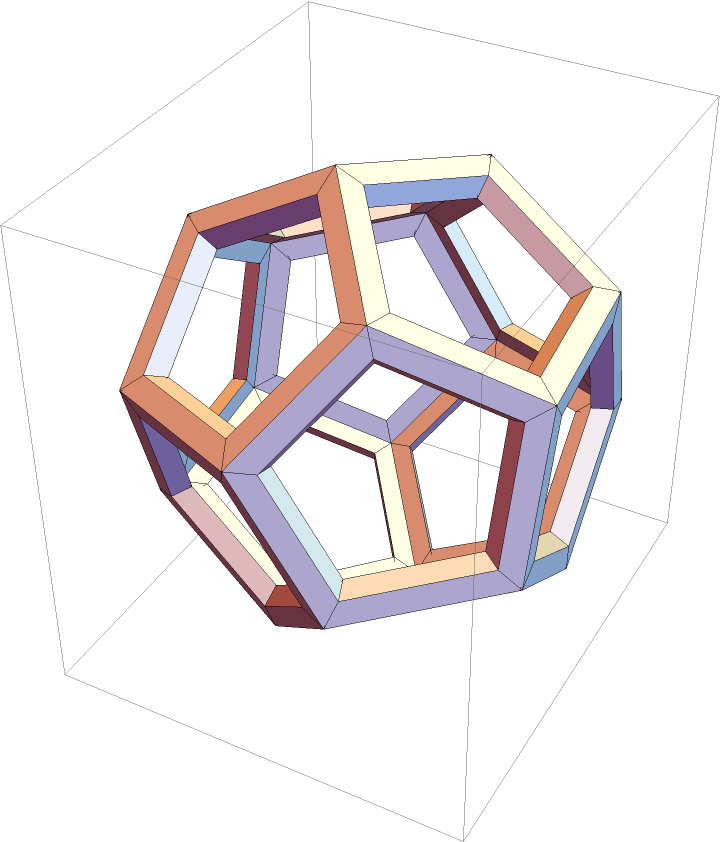 |
| In[5]:= |
| Out[5]= | 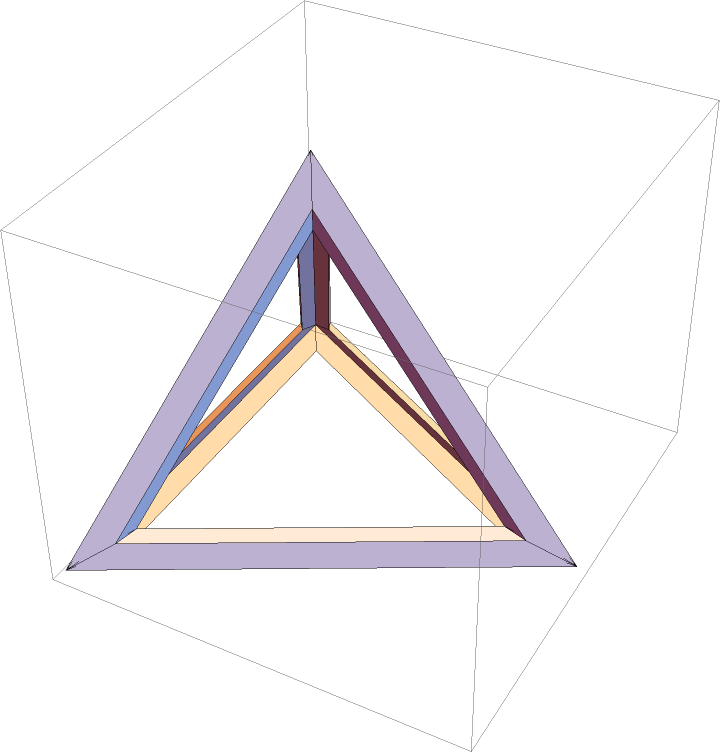 |
A Polyhedron with voids:
| In[6]:= |
| Out[6]= | 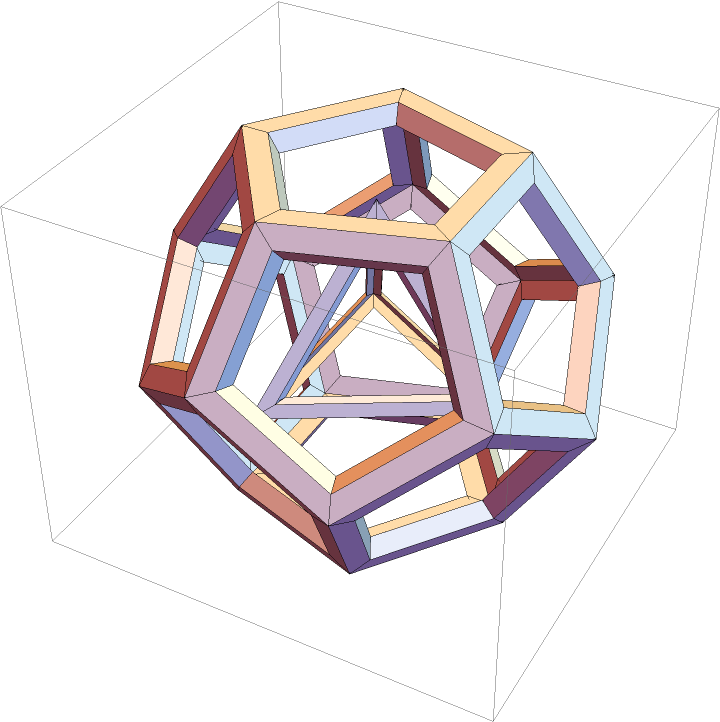 |
Add a texture:
| In[7]:= |  |
| In[8]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/f15e073d-8bc3-4642-8036-fd18a30907e7"]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/1f99f04b578e62be.png) |
| Out[8]= |  |
| In[9]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/c8e07d98-401c-428c-9153-75b84d1a7bab"]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/4e87f938173e992d.png) |
| Out[9]= | 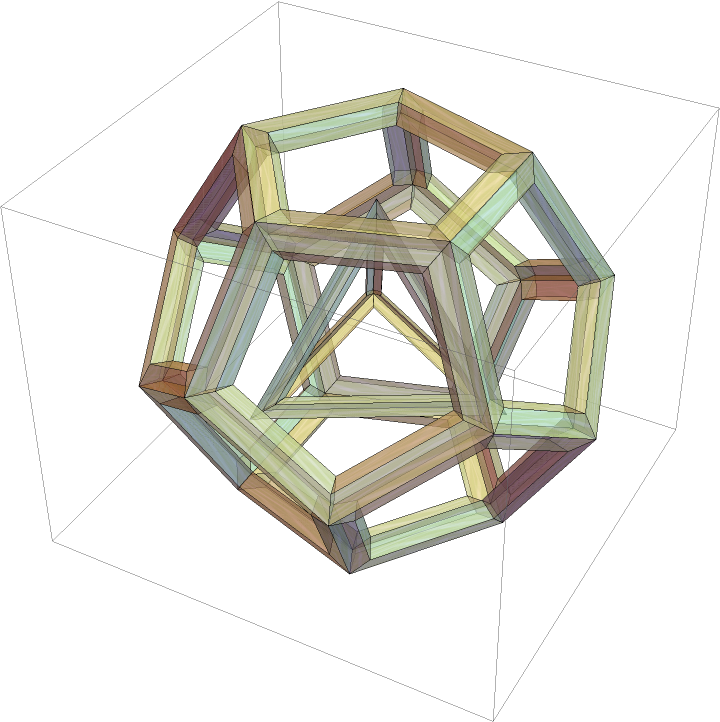 |
Use VertexColors:
| In[10]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9503143b-cb3d-42dc-b6a0-4bc74d8f67c4"]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/545ae2c144d69913.png) |
| Out[10]= |  |
| In[11]:= | ![ResourceFunction["OutlinePolygons"][
Graphics3D[
Polyhedron[{{0, 0, Sqrt[2/3] - 1/(2 Sqrt[6])}, {-(1/(2 Sqrt[3])), -(1/2), -(1/(
2 Sqrt[6]))}, {-(1/(2 Sqrt[3])), 1/2, -(1/(2 Sqrt[6]))}, {1/
Sqrt[3], 0, -(1/(2 Sqrt[6]))}}, {{2, 3, 4}, {3, 2, 1}, {4, 1, 2}, {1, 4, 3}}, VertexColors -> {Red, Green, Yellow, Blue}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/2992d23207b03b69.png) |
| Out[11]= | 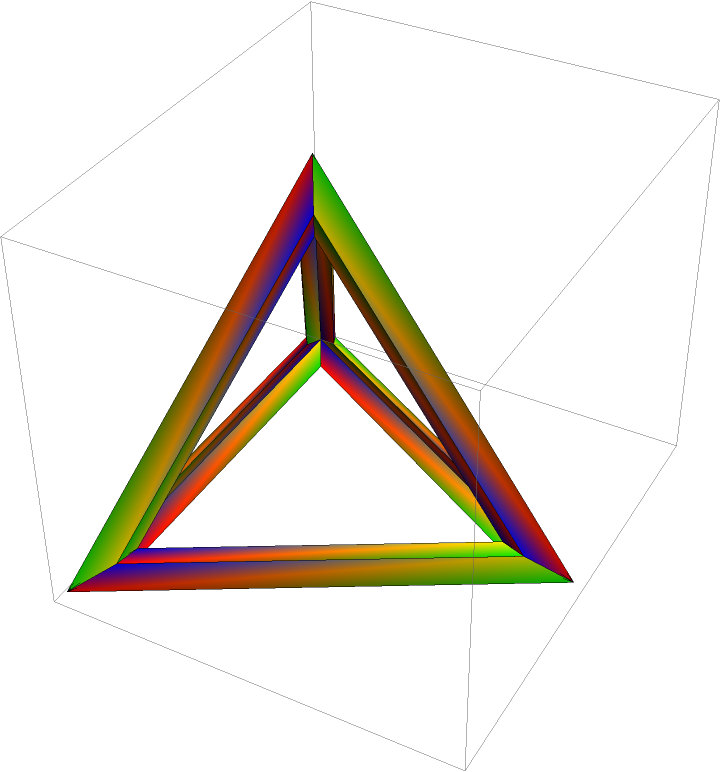 |
Use VertexNormals:
| In[12]:= |
| In[13]:= | ![Graphics3D[{Yellow, Polyhedron[{{0, 0, Sqrt[2/3] - 1/(2*Sqrt[6])}, {-1/(2*Sqrt[3]), -1/
2, -1/(2*Sqrt[6])}, {-1/(2*Sqrt[3]), 1/2, -1/(2*Sqrt[6])}, {1/Sqrt[3], 0, -1/(2*Sqrt[6])}}, {{2, 3, 4}, {3, 2, 1}, {4, 1, 2}, {1, 4, 3}}, VertexNormals -> {-n, n, n, n}]}] // ResourceFunction[
"OutlinePolygons"]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/21b01a9e90d9e9a2.png) |
| Out[13]= | 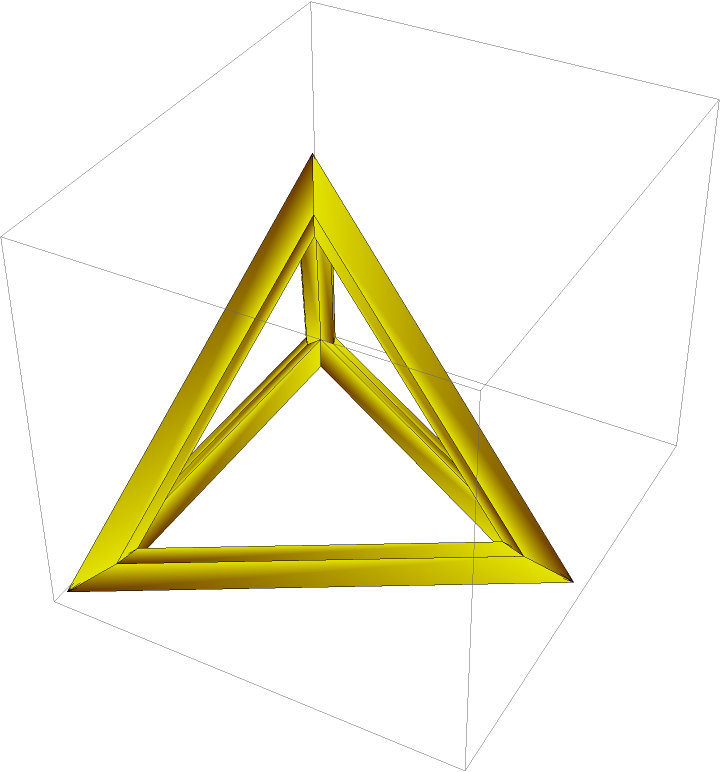 |
Use Scaled coordinates:
| In[14]:= | ![ResourceFunction["OutlinePolygons"][
Graphics3D[
Polyhedron[{{Scaled[{0.2, 0., 0.3}], Scaled[{0.2, 0.9, 0.3}], Scaled[{1, 0.5, 0.3}]}, {Scaled[{0.2, 0.9, 0.3}], Scaled[{0.2, 0., 0.3}], Scaled[{0.5, 0.5, 1.}]}, {Scaled[{1, 0.5, 0.3}], Scaled[{0.5, 0.5, 1.}], Scaled[{0.2, 0., 0.3}]}, {Scaled[{0.5, 0.5, 1.}], Scaled[{1, 0.5, 0.3}], Scaled[{0.2, 0.9, 0.3}]}}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/20ef94f6f15a78ac.png) |
| Out[14]= | 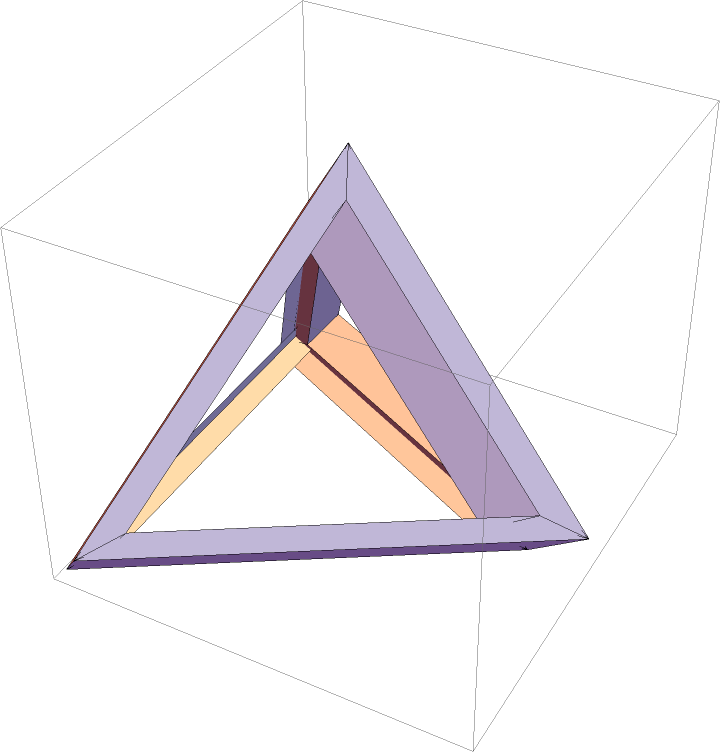 |
Create a periodic structure:
| In[15]:= | ![uehp = Graphics3D[{#, Translate[#, {0, 1.732, 0}], Translate[#, {2, 0, 0}], Translate[#, {2, 1.732, 0}]} &@(Entity["Polyhedron", {"Prism", 6}]["Graphics3D"] // ResourceFunction["PerforatePolygons"] // ResourceFunction[
"OutlinePolygons"])[[1]], Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/7a42a7ee1d6bfdef.png) |
| Out[15]= | 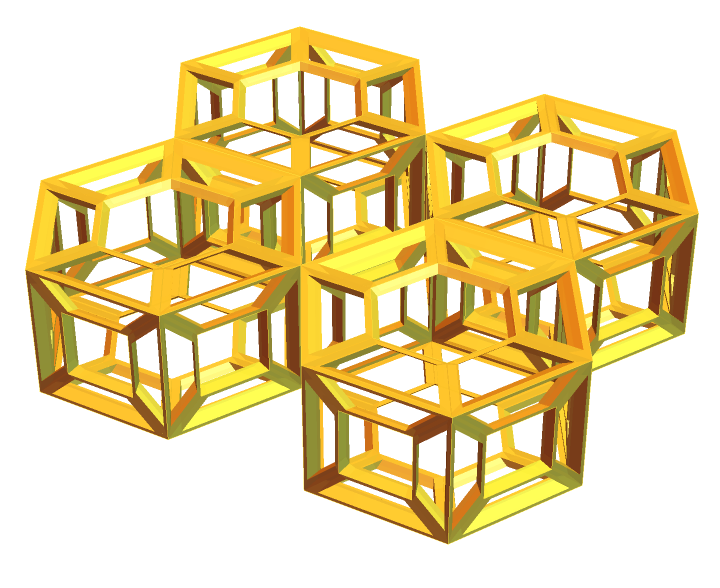 |
Outline a Klein bottle:
| In[16]:= | ![KleinBottle[{A_, B_, C_}, {s_, t_}] := {Piecewise[{{A Cos[s] (1 + Sin[s]) + B (1 - Cos[s]/2) Cos[s] Cos[t], 0 <= s <= Pi}, {A Cos[s] (1 + Sin[s]) + B (1 - Cos[s]/2) Cos[t + \[Pi]], Pi <= s <= 2 Pi}}], Piecewise[{{C Sin[s] + B (1 - Cos[s]/2) Sin[s] Cos[t], 0 <= s <= Pi}, {C Sin[s], Pi <= s <= 2 Pi}}], B (1 - Cos[s]/2) Sin[t]}](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/3d02edf624c9af45.png) |
| In[17]:= | ![ResourceFunction["OutlinePolygons"][
With[{S = 3.415, \[Rho]s = 0.258`, \[Rho]t = 0.338`}, ParametricPlot3D[
KleinBottle[{6, 6, 19}, {s, t}], {s, 0, 2 \[Pi]}, {t, 0, 2 \[Pi]}, Exclusions -> None, PlotStyle -> Opacity[0.8`], PerformanceGoal -> "Quality", Mesh -> None, RegionFunction -> (! (#4 - S)^2/\[Rho]s^2 + (#5 - Pi)^2/\[Rho]t^2 <
1 &), Boxed -> False, Axes -> False]]]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/3f51478b7963975a.png) |
| Out[17]= |  |
A 3D model of Beethoven:
| In[18]:= |
| Out[18]= |  |
Compute the circumsphere of a platonic solid, solving for edge length l, then the insphere, and let be the circumsphere of the next:
| In[19]:= |
| In[20]:= | ![kmc = Flatten[
Prepend[MapThread[{#1[#2[[1]]], Sphere[{0, 0, 0}, #2[[2]]]} &, {ps, FoldList[
With[{length = Solve[Last[Circumsphere[#2[l]]] == #1[[2]]][[1, 1, 2]]}, {length, Last[Insphere[#2[length]]]}] &, {1, 1/2}, Rest[ps]] // FullSimplify}], Sphere[{0, 0, 0}, Sqrt[3]/2]]]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/190b93018bba0dbb.png) |
| Out[20]= |  |
Kepler’s Mysterium Cosmographicum:
| In[21]:= | ![Manipulate[
ResourceFunction["OutlinePolygons"][
Graphics3D[{Opacity[0.5], Take[Reverse@kmc, n]}, Boxed -> False, ClipPlanes -> If[cp, InfinitePlane[{{0, 0, 0}, {1, 1, 0}, {-1, -2, 0}}], None]]], {{n, 6, "zoom out"}, 1, 11, 1}, {{cp, True, "clip plane"}, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/76c/76cc61f7-7106-4d6a-9edb-784a5d815170/0239dcb3e988cea4.png) |
| Out[21]= | 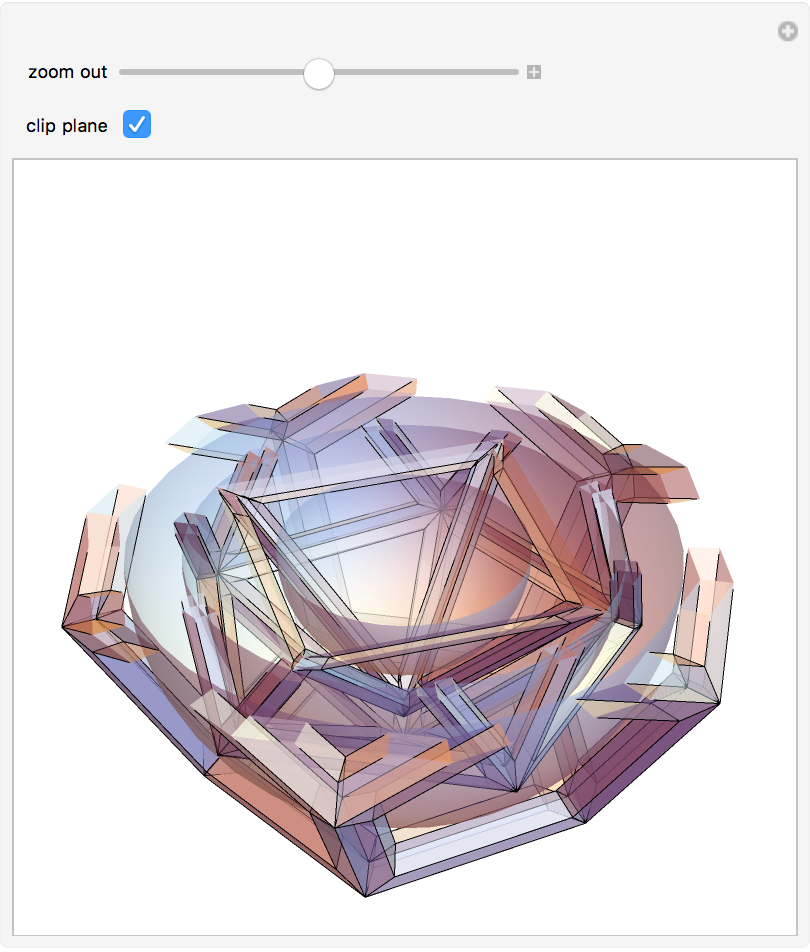 |
This work is licensed under a Creative Commons Attribution 4.0 International License