Function Repository Resource:

PolynomialFitCurve

Source Notebook

Polynomial fit of a given set of data, represented as a spline curve

Contributed by: Jan Mangaldan

ResourceFunction["PolynomialFitCurve"][{{x₁,y₁},{x₂,y₂},…},n]

returns a BSplineCurve representing the least-squares, degree-n polynomial fit of the points {x_i,y_i}.

Examples

Basic Examples (3)

Here is some data:

In[1]:=

A BSplineCurve representing a quadratic fit to the data:

In[2]:=

Out[2]=

Show the data and the polynomial fit together:

In[3]:=

Out[3]=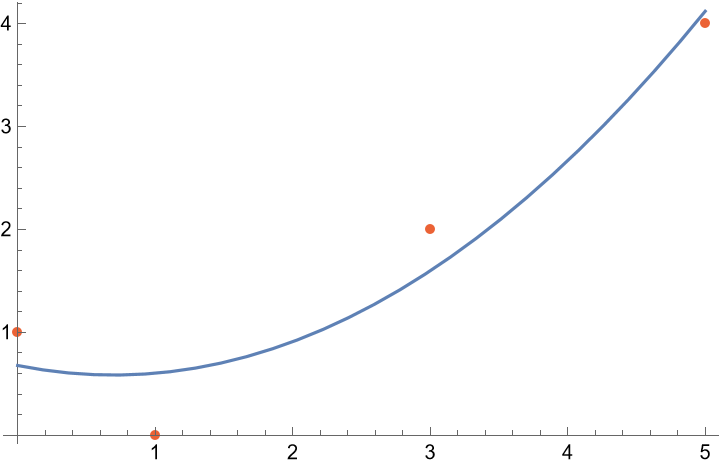

Scope (1)

Compare cubic and quartic polynomial fits to a set of data:

In[4]:=

data = {{0, 0}, {0.1, 0.3}, {0.5, 0.4}, {1, -0.2}, {2, 3}};
Legended[ListPlot[data, Prolog -> {{Directive[
RGBColor[0.560181, 0.691569, 0.194885],
AbsoluteThickness[2]], ResourceFunction["PolynomialFitCurve"][data, 3]}, {Directive[
RGBColor[0.922526, 0.385626, 0.209179],
AbsoluteThickness[2]], ResourceFunction["PolynomialFitCurve"][data, 4]}}], LineLegend[{RGBColor[0.560181, 0.691569, 0.194885], RGBColor[
0.922526, 0.385626, 0.209179]}, {"degree 3", "degree 4"}]]

Out[5]=

Properties and Relations (2)

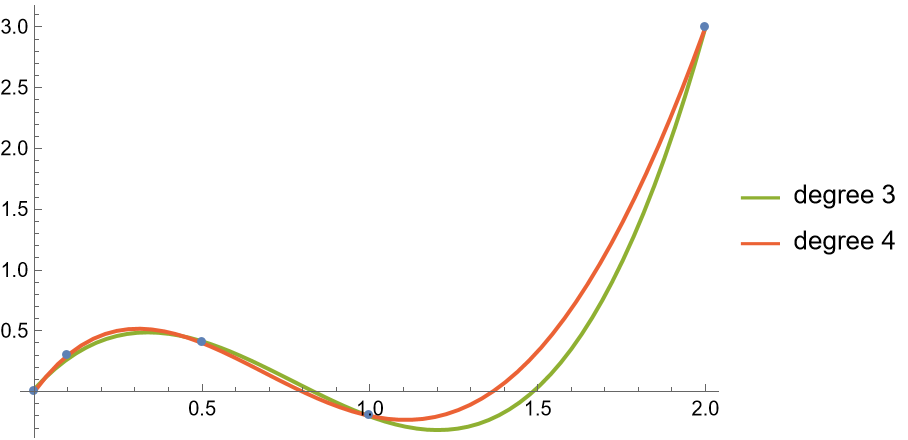Here is some data:

In[6]:=

For degree 1, PolynomialFitCurve gives a result equivalent to the result of the resource function TrendLine:

In[7]:=

$c1 = ResourceFunction["PolynomialFitCurve"][data, 1]; c2 = ResourceFunction["TrendLine"][data]; Graphics[{{Directive[ AbsoluteThickness[4], RGBColor[0.368417, 0.506779, 0.709798]], c1}, {Directive[ AbsoluteThickness[2], RGBColor[0.880722, 0.611041, 0.142051]], c2}, {Directive[ AbsolutePointSize[6], RGBColor[0.922526, 0.385626, 0.209179]], Point[data]}}, {AspectRatio -> GoldenRatio^(-1), Axes -> True}]$

Out[8]=

Requirements

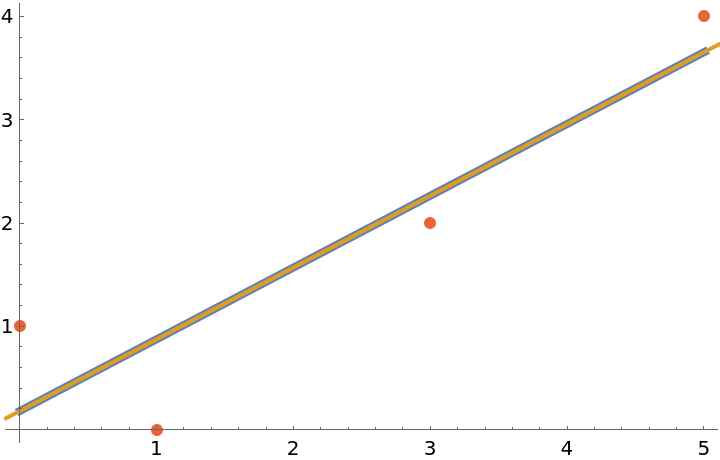Wolfram Language 12.3 (May 2021) or above

Version History

1.0.0 – 03 January 2024

Related Resources

Author Notes

Polynomial fits corresponding to other fitting norms (e.g. 1, ∞) will be implemented in a future version.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License