Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Reflect a polyhedron over a given face
ResourceFunction["PolyhedronFaceReflect"][polyhedron,k] reflects polyhedron over its kth face. |
In the octahedron given below, a list of vertices is followed by a list of faces (vertex indices):
| In[1]:= | ![octa = Polyhedron[{{-1, 0, 0}, {0, -1, 0}, {0, 0, -1}, {0, 0, 1}, {0, 1, 0}, {1, 0, 0}}, {{1, 2, 4}, {1, 3, 2}, {1, 4, 5}, {1, 5, 3}, {2, 3, 6}, {2, 6, 4}, {3, 5, 6}, {4, 6, 5}}];](https://www.wolframcloud.com/obj/resourcesystem/images/677/6778fcb6-09cf-425e-9a08-a5243c18c2de/20b8a3d6e282c8fb.png) |
Reflect the octahedron over its first face:
| In[2]:= |
| Out[2]= |  |
Make a ring of eight octahedra:
| In[3]:= |
| Out[3]= | 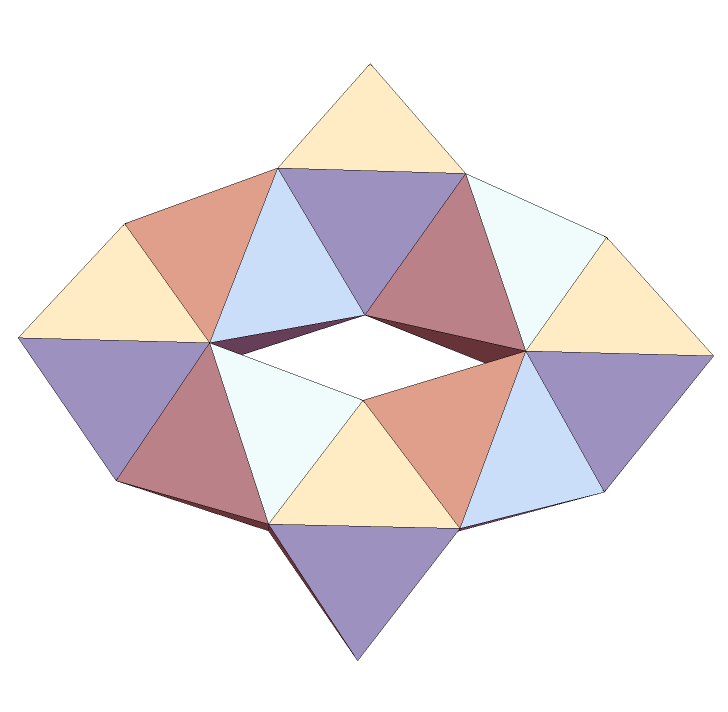 |
Reflect a dodecahedron over its first face:
| In[4]:= | ![dod = Dodecahedron[];
Graphics3D[{Opacity[2/3], dod, ResourceFunction["PolyhedronFaceReflect"][dod, 1] }, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/677/6778fcb6-09cf-425e-9a08-a5243c18c2de/2b481197cf6a0316.png) |
| Out[5]= | 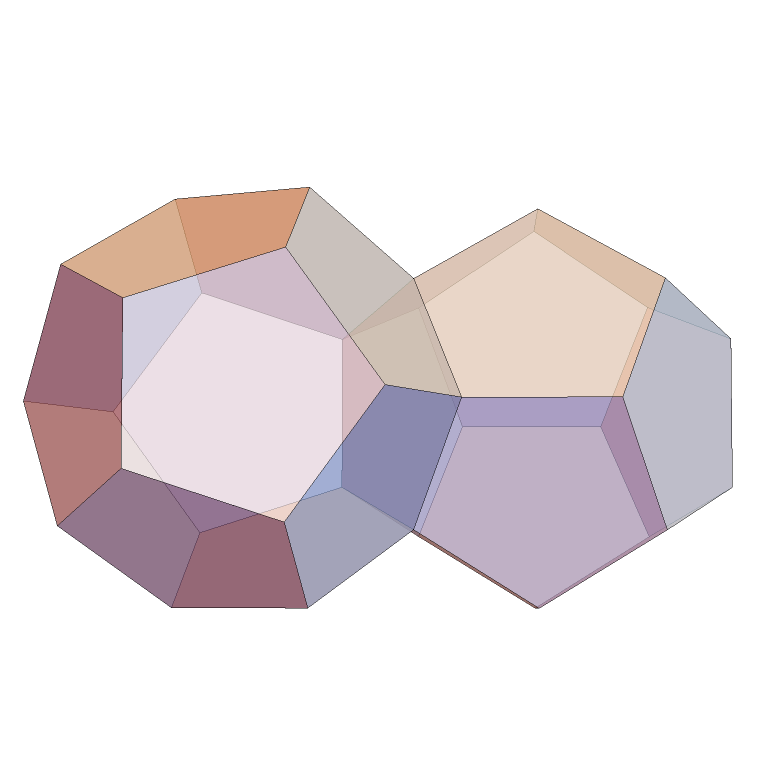 |
Reflect the snub disphenoid over its fifth face:
| In[6]:= | ![snub = PolyhedronData["SnubDisphenoid", "Polyhedron"];
Graphics3D[{Opacity[2/3], snub, ResourceFunction["PolyhedronFaceReflect"][snub, 5] }, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/677/6778fcb6-09cf-425e-9a08-a5243c18c2de/0623e53b23cd9266.png) |
| Out[7]= | 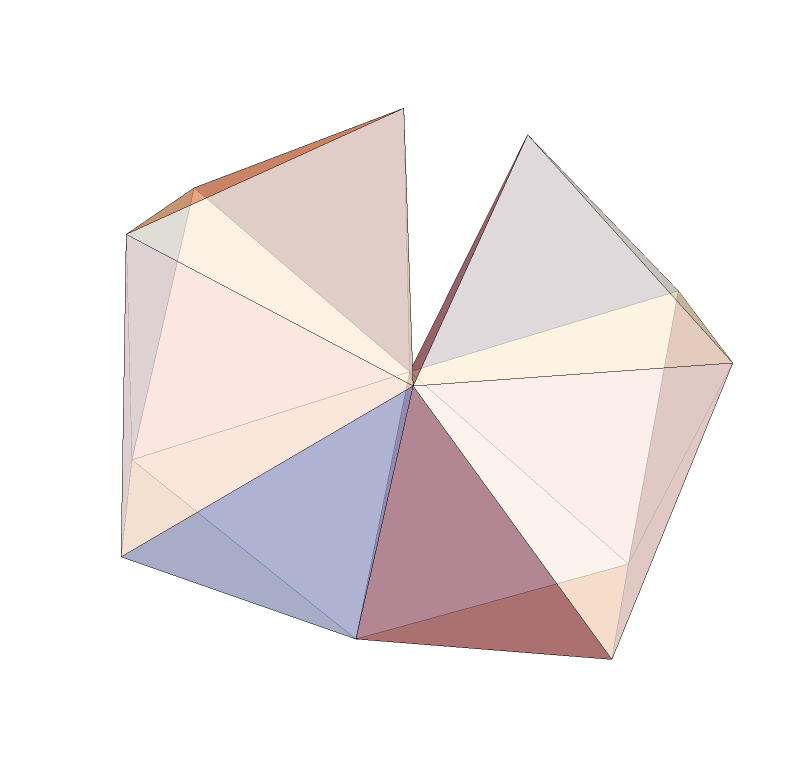 |
Make a perfect ring of twelve 4-antiprisms:
| In[8]:= | ![anti4 = Polyhedron[{{1, -1,
Root[-1 + 2 #^4& , 1, 0]}, {-1, -1,
Root[-1 + 2 #^4& , 1, 0]}, {-1, 1,
Root[-1 + 2 #^4& , 1, 0]}, {1, 1,
Root[-1 + 2 #^4& , 1, 0]}, {2^Rational[1, 2], 0,
Root[-1 + 2 #^4& , 2, 0]}, {0, 2^Rational[1, 2],
Root[-1 + 2 #^4& , 2, 0]}, {-2^Rational[1, 2], 0,
Root[-1 + 2 #^4& , 2, 0]}, {0, -2^Rational[1, 2],
Root[-1 + 2 #^4& , 2, 0]}}, {{1, 2, 3, 4}, {5, 6, 7, 8}, {1, 8, 2}, {
2, 7, 3}, {3, 6, 4}, {4, 5, 1}, {1, 5, 8}, {2, 8, 7}, {3, 7, 6}, {
4, 6, 5}}];
Graphics3D[
FoldList[ResourceFunction["PolyhedronFaceReflect"], anti4, {10, 1, 8, 9, 1, 7, 8, 1, 10, 7, 1}], Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/677/6778fcb6-09cf-425e-9a08-a5243c18c2de/281ffdbd28acbadc.png) |
| Out[9]= | 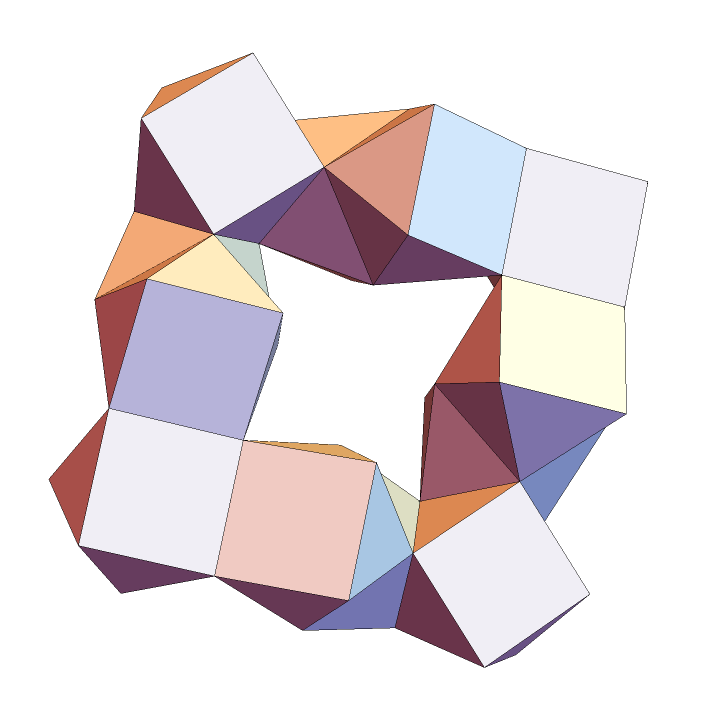 |
Make a spiral of tetrahedra (the Boerdijk–Coxeter helix):
| In[10]:= | ![Graphics3D[
FoldList[ResourceFunction["PolyhedronFaceReflect"], Tetrahedron[], {1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4}], Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/677/6778fcb6-09cf-425e-9a08-a5243c18c2de/67ecb8c12883e75f.png) |
| Out[10]= | 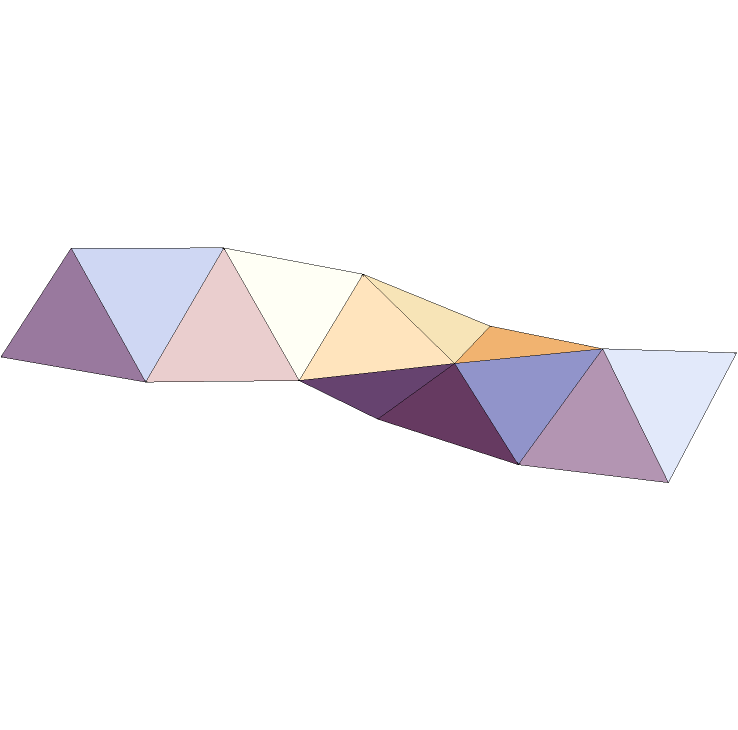 |
Compare with the result of TetrahelixMesh:
| In[11]:= |
| Out[11]= | 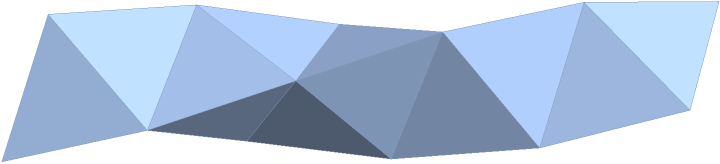 |
Make a chain of icosahedra:
| In[12]:= |
| Out[12]= | 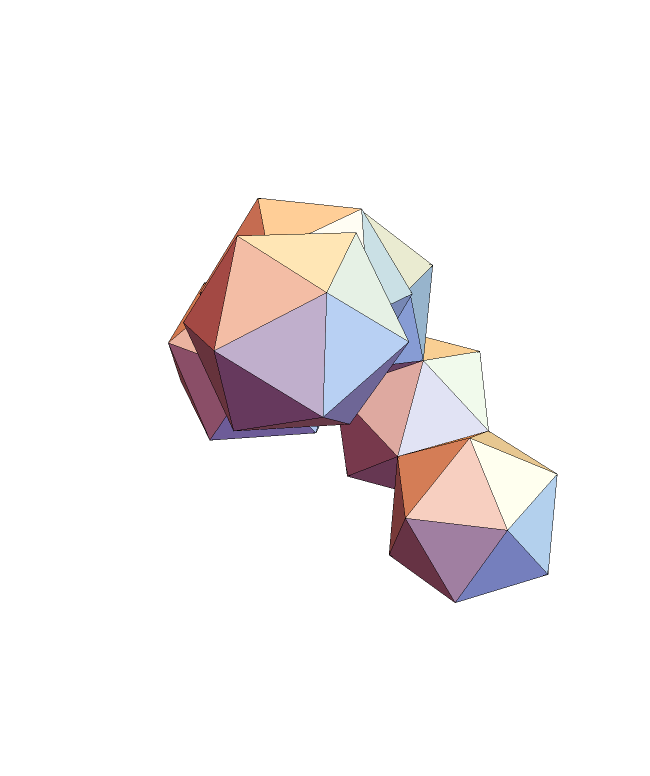 |
This work is licensed under a Creative Commons Attribution 4.0 International License