Function Repository Resource:

PolyhedralGraphFaces

Source Notebook

Get the faces corresponding to a polyhedral graph

Contributed by: Ed Pegg Jr

ResourceFunction["PolyhedralGraphFaces"][edges]

returns the corresponding faces of polyhedron from the list of edges of a polyhedral graph.

Details

This function is meant purely for polyhedral graphs, as a method for turning them into polyhedra.

Currently, faces returned may not be flat with the given set of vertices.

In the future, this may be expanded to cycle double covers for bridgeless graphs, where every edge is covered by two cycles.

Examples

Basic Examples (2)

Find the faces corresponding to a set of polyhedral graph edges:

In[1]:=

Out[1]=

Show the faces:

In[2]:=

Out[2]=

Show the Schlegel diagram or Tutte embedding of the polyhedral graph:

In[3]:=

Out[3]=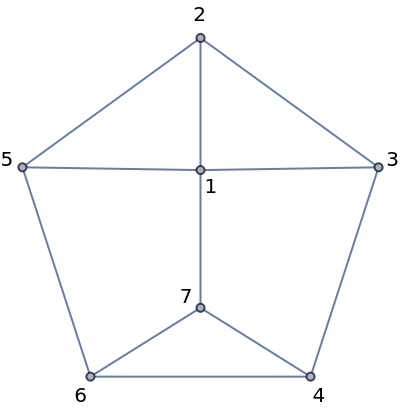

Show the polyhedral graph as a polyhedron:

In[4]:=

Out[4]=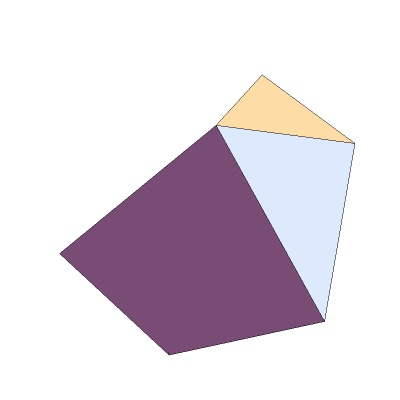

Create a Polyhedron directly from a polyhedral Graph:

In[5]:=

$poly = ResourceFunction["PolyhedralGraphFaces"][\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4, 5, 6, 7}, {Null, {{1, 2}, {1, 3}, {1, 5}, {1, 7}, {2, 3}, {2, 5}, { 3, 4}, {4, 6}, {4, 7}, {5, 6}, {6, 7}}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{0.880806378907739, 0.8316050882637749}, {0., 0.8303917665081879}, { 0.6265105580039326, 0.}, {1.7264095173822114`, 0.22771610658092223`}, {0.6241760994998922, 1.6624372813870716`}, {1.726207414637839, 1.4360545067496597`}, {2.1162340009509673`, 0.8316148891744471}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1, 2}, {1, 3}, {1, 5}, {1, 7}, {2, 3}, {2, 5}, {3, 4}, {4, 6}, {4, 7}, {5, 6}, {6, 7}}, 0.02354764731732295]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02354764731732295], DiskBox[2, 0.02354764731732295], DiskBox[3, 0.02354764731732295], DiskBox[4, 0.02354764731732295], DiskBox[5, 0.02354764731732295], DiskBox[6, 0.02354764731732295], DiskBox[7, 0.02354764731732295]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->"NetworkGraphics", FormatType->TraditionalForm, FrameTicks->None]\)]$