Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Identify which polar curves are associated with the given equations
ResourceFunction["PolarCurveIdentifier"][eq,{r,t}] returns the name of a polar curve that best describes the polar equation eq with radius variable r and angle variable t. | |
ResourceFunction["PolarCurveIdentifier"][eq,{u,v},system] first converts eq with variables u and v from coordinate system system to polar coordinates. | |
ResourceFunction["PolarCurveIdentifier"][{eq1,eq2,…},{r,t},system] returns a list of the names of polar curves corresponding to each equation eqi. | |
ResourceFunction["PolarCurveIdentifier"]["CurveTypes"] returns a list of all the available curve names. |
Identify that a fixed radius corresponds to a circle:
| In[1]:= |
| Out[1]= |
Identify that a fixed angle corresponds to a line:
| In[2]:= |
| Out[2]= |
Identify the polar curve with a radius of zero:
| In[3]:= |
| Out[3]= |
Return a list of all possible outputs:
| In[4]:= |
| Out[4]= | 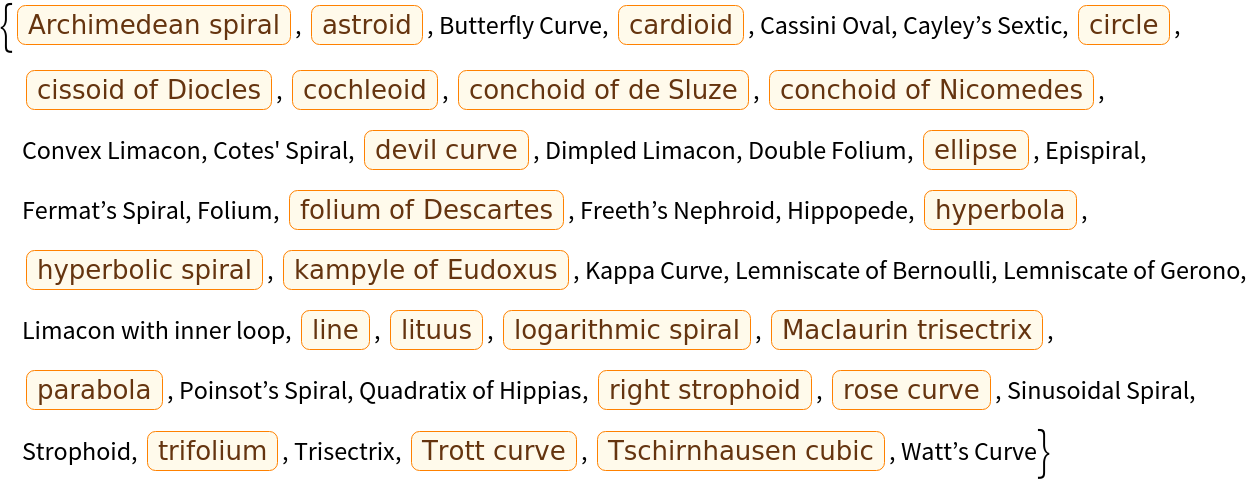 |
Multiple equations can be input as a list:
| In[5]:= |
| Out[5]= |
Some polar curves do not have known names:
| In[6]:= |
| Out[6]= |
The MaxItems option determines the maximum number of names given for each curve. Find up to five families each for three curves:
| In[7]:= |
| Out[7]= |
Find up to two families for a single curve:
| In[8]:= |
| Out[8]= |
Find all possible families:
| In[9]:= |
| Out[9]= |
The starting coordinate system can be changed:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
Equations do not need to be solved for the radius before being identified:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
For a family of equations, the visual difference in the respective curves is apparent:
| In[14]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= |  |
If variables appear other than those specified, the function is left unevaluated:
| In[16]:= |
| Out[16]= |
Equations must be given as an equality:
| In[17]:= |
| Out[17]= |
Improper MaxItems values will cause the function to return unevaluated:
| In[18]:= |
| Out[18]= |
Multiple curve types intersect simultaneously:
| In[19]:= |
| Out[19]= |
Some curves have different subtypes:
| In[20]:= |
| Out[20]= |
| In[21]:= | ![ResourceFunction["PolarCurveIdentifier", ResourceVersion->"1.0.0"][{r == 4 Cos[t] Sin[t]^2 - 2 Cos[t], r == 4 Cos[t] Sin[t]^2, r == Cos[t] (4 Sin[t]^2 - 1)}, {r, t}]](https://www.wolframcloud.com/obj/resourcesystem/images/02d/02daf483-3d5b-4b31-8509-32a53eb7207b/1-0-0/7579ae7385fc13e6.png) |
| Out[21]= |
There are several ways to express Cotes' Spiral:
| In[22]:= |
| Out[22]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License