Function Repository Resource:

PolarCurveIdentifier

Identify which polar curves are associated with the given equations

Contributed by: Garrett Dubofsky, Wolfram|Alpha Math Team

ResourceFunction["PolarCurveIdentifier"][eq,{r,t}]

returns the name of a polar curve that best describes the polar equation eq with radius variable r and angle variable t.

ResourceFunction["PolarCurveIdentifier"][eq,{u,v},system]

first converts eq with variables u and v from coordinate system system to polar coordinates.

ResourceFunction["PolarCurveIdentifier"][{eq₁,eq₂,…},{r,t},system]

returns a list of the names of polar curves corresponding to each equation eq_i.

ResourceFunction["PolarCurveIdentifier"]["CurveTypes"]

returns a list of all the available curve names.

Details

Setting the option MaxItems to a positive integer or All will increase the maximum number of returned curve names.

Equations must be of the form f[r,t]==g[r,t].

With a few exceptions, multiple curve names are ordered from smallest to largest families of curves.

When possible, curve names are returned as PlaneCurve entities.

Only coordinate systems of two variables are supported.

Examples

Basic Examples (4)

Identify that a fixed radius corresponds to a circle:

In[1]:=

Out[1]=

Identify that a fixed angle corresponds to a line:

In[2]:=

Out[2]=

Identify the polar curve with a radius of zero:

In[3]:=

Out[3]=

Return a list of all possible outputs:

In[4]:=

Out[4]=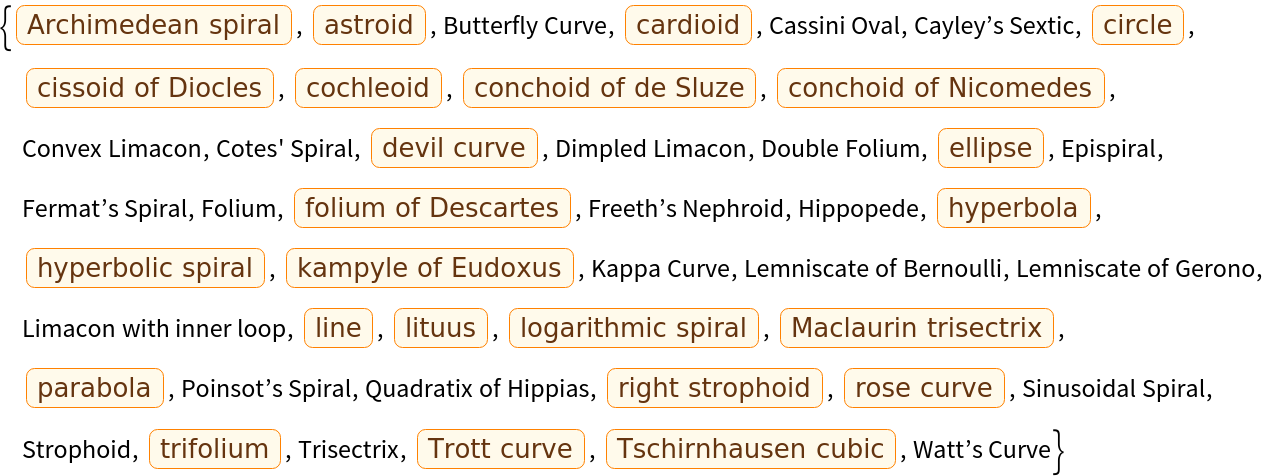

Scope (2)

Multiple equations can be input as a list:

In[5]:=

$ResourceFunction[ "PolarCurveIdentifier"][{r == Cos[2 t], 1/r == 3 t, r^2 == t^2}, {r, t}]$

Out[5]=

Some polar curves do not have known names:

In[6]:=

Out[6]=

Options (3)

The MaxItems option determines the maximum number of names given for each curve. Find up to five families each for three curves:

In[7]:=

$ResourceFunction[ "PolarCurveIdentifier"][{r == Cos[2 t], 1/r == 3 t, r^2 == t^2}, {r, t}, MaxItems -> 5]$

Out[7]=

Find up to two families for a single curve:

In[8]:=

Out[8]=

Find all possible families:

In[9]:=

Out[9]=

The starting coordinate system can be changed:

In[10]:=

$ResourceFunction[ "PolarCurveIdentifier"][{x^2 + y^2 == 3}, {x, y}, "Cartesian"]$

Out[10]=

In[11]:=

Out[11]=

Equations do not need to be solved for the radius before being identified:

In[12]:=

$ResourceFunction["PolarCurveIdentifier"][r == -Cos[3 t]^(1/3), {r, t}]$

Out[12]=

In[13]:=

$ResourceFunction["PolarCurveIdentifier"][Cos[3 t] == -r^3, {r, t}]$

Out[13]=

Applications (1)

For a family of equations, the visual difference in the respective curves is apparent:

In[14]:=

Out[14]=

In[15]:=

$PolarPlot[1/(1 + # Cos[t]), {t, 0, 2 \[Pi]}, AspectRatio -> 1, Exclusions -> All] & /@ {0, 1/2, 1, 3/2}$

Out[15]=

Possible Issues (3)

If variables appear other than those specified, the function is left unevaluated:

In[16]:=

Out[16]=

Equations must be given as an equality:

In[17]:=

Out[17]=

Improper MaxItems values will cause the function to return unevaluated:

In[18]:=

Out[18]=

Neat Examples (3)

Multiple curve types intersect simultaneously:

In[19]:=

Out[19]=

Some curves have different subtypes:

In[20]:=

Out[20]=

In[21]:=

$ResourceFunction[ "PolarCurveIdentifier"][{r == 4 Cos[t] Sin[t]^2 - 2 Cos[t], r == 4 Cos[t] Sin[t]^2, r == Cos[t] (4 Sin[t]^2 - 1)}, {r, t}]$

Out[21]=

There are several ways to express Cotes' Spiral:

In[22]:=

Out[22]=

Publisher

Wolfram|Alpha Math Team

Version History

2.0.0 – 23 March 2023
1.0.0 – 06 January 2023

Source Metadata

Citation:
- Weisstein, Eric. “Wolfram MathWorld: The Web’s Most Extensive Mathematics Resource.”, Wolfram, https://mathworld.wolfram.com.

Related Resources

Author Notes

Conflicts in curve definitions were resolved by using those on Wolfram MathWorld.

To view the full source code for PolarCurveIdentifier, evaluate the following:

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

PolarCurveIdentifier

Details