Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PivotedLUDecomposition

Source Notebook

Compute the LU decomposition of a matrix with different pivoting methods

Contributed by: Jan Mangaldan

ResourceFunction["PivotedLUDecomposition"][m]

generates a representation of the LU decomposition of a matrix m.

Details and Options

ResourceFunction["PivotedLUDecomposition"] returns a list of three elements. The first element is a combination of upper‐ and lower‐triangular matrices, and the second and third elements are permutation vectors respectively specifying rows and columns used for pivoting.
ResourceFunction["PivotedLUDecomposition"] takes a Pivoting option. Possible settings include:
"Complete"use complete pivoting
"Partial"use partial pivoting (equivalent to LUDecomposition)
"Rook"use rook pivoting (default)
In partial pivoting, rows are interchanged such that the row containing the entry with the largest magnitude from the currently active column of the matrix is swapped with the current row, while columns are not interchanged.
In complete pivoting, rows and columns are interchanged such that the entry with the largest magnitude in the entire active submatrix becomes the pivot element.
In rook pivoting, rows and columns are interchanged such that the entry with the largest magnitude in the row and column where it belongs becomes the pivot element. Stated differently, the potential pivots are taken from the positions in the active submatrix that are visible to a rook chesspiece.

Examples

Basic Examples (4) 

Compute the LU decomposition of a matrix:

In[1]:=
{lu, rp, cp} = ResourceFunction["PivotedLUDecomposition"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "1", "1"}, {"2", "4", "8"}, {"3", "9", "27"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]
Out[1]=

l is the strictly lower triangular part of lu with ones assumed along the diagonal:

In[2]:=
MatrixForm[l = LowerTriangularize[lu, -1] + IdentityMatrix[3]]
Out[2]=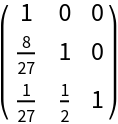

u is the upper triangular part of lu:

In[3]:=
MatrixForm[u = UpperTriangularize[lu]]
Out[3]=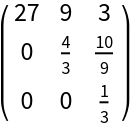

Multiplying l and u gives a permuted version of the original matrix, with the permutations determined by rp and cp. Verify the decomposition:

In[4]:=
l . u == \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "1", "1"}, {"2", "4", "8"}, {"3", "9", "27"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)[[rp, cp]]
Out[4]=

Scope (3) 

Find the LU decomposition of a machine-precision matrix:

In[5]:=
m = {{1.6, 2.7, 3.6}, {1.2, 3.2, 5.2}, {3.3, 3.4, 6.5}}; {lu, rp, cp} = ResourceFunction["PivotedLUDecomposition"][m]
Out[6]=

Verify the decomposition:

In[7]:=
{l, u} = {LowerTriangularize[lu, -1] + IdentityMatrix[3], u = UpperTriangularize[lu]}; l . u == m[[rp, cp]]
Out[8]=

LU decomposition for a complex matrix:

In[9]:=
ResourceFunction["PivotedLUDecomposition"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"2", "+", RowBox[{"4", " ", "I"}]}], RowBox[{"9", "+", RowBox[{"9", " ", "I"}]}], RowBox[{"9", "+", RowBox[{"2", " ", "I"}]}]}, { RowBox[{"2", "+", RowBox[{"9", " ", "I"}]}], RowBox[{"1", "+", RowBox[{"3", " ", "I"}]}], RowBox[{"4", " ", "I"}]}, { RowBox[{"3", "+", RowBox[{"8", " ", "I"}]}], "0", RowBox[{"7", "+", RowBox[{"4", " ", "I"}]}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]
Out[9]=

LU decomposition of a non-square matrix:

In[10]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"4", "4", "1", "4"}, {"1", "4", "1", "7"}, {"7", "5", "6", "3"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\); {lu, rp, cp} = ResourceFunction["PivotedLUDecomposition"][m]
Out[11]=

Reconstruct the l and u matrices:

In[12]:=
s = Min[{p, q} = Dimensions[lu]]; MatrixForm[ l = PadRight[LowerTriangularize[lu, -1], {p, s}] + IdentityMatrix[{p, s}]]
Out[13]=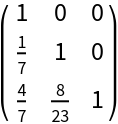
In[14]:=
MatrixForm[u = PadRight[UpperTriangularize[lu], {s, q}]]
Out[14]=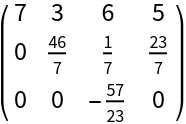

Verify the decomposition:

In[15]:=
l . u == \!\(\* TagBox["m", Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)[[rp, cp]]
Out[15]=

Options (1) 

Pivoting (1) 

Use different pivoting methods in computing the LU decomposition:

In[16]:=
ResourceFunction["PivotedLUDecomposition"][\!\(\* TagBox[ TagBox[ RowBox[{"(", "", GridBox[{ {"3", "1", "5"}, {"2", "4", "6"}, {"8", "7", "9"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), Pivoting -> "Complete"]
Out[16]=
In[17]:=
ResourceFunction["PivotedLUDecomposition"][\!\(\* TagBox[ TagBox[ RowBox[{"(", "", GridBox[{ {"3", "1", "5"}, {"2", "4", "6"}, {"8", "7", "9"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), Pivoting -> "Partial"]
Out[17]=
In[18]:=
ResourceFunction["PivotedLUDecomposition"][\!\(\* TagBox[ TagBox[ RowBox[{"(", "", GridBox[{ {"3", "1", "5"}, {"2", "4", "6"}, {"8", "7", "9"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), Pivoting -> "Rook"]
Out[18]=

Applications (5) 

LU decompositions are mainly used to solve linear systems. Here is a 5×5 random matrix:

In[19]:=
m = RandomReal[1, {5, 5}];

Compute its LU decomposition:

In[20]:=
{lu, rp, cp} = ResourceFunction["PivotedLUDecomposition"][m];

Extract the lower and upper parts of the decomposition:

In[21]:=
l = LowerTriangularize[lu, -1] + IdentityMatrix[5]; u = UpperTriangularize[lu];

Solve the system m.x=b for x with two backsolves and two permutations:

In[22]:=
b = ConstantArray[1, 5]; y = LinearSolve[l, b[[rp]]]; x = Permute[LinearSolve[u, y], cp]
Out[23]=

Compute the residual, which should be tiny:

In[24]:=
Norm[m . x - b, \[Infinity]]
Out[24]=

Properties and Relations (1) 

With the setting Pivoting→"Partial", PivotedLUDecomposition is equivalent to the built-in LUDecomposition:

In[25]:=
ResourceFunction["PivotedLUDecomposition"][\!\(\* TagBox[ TagBox[ RowBox[{"(", "", GridBox[{ {"3", "1", "5"}, {"2", "4", "6"}, {"8", "7", "9"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), Pivoting -> "Partial"]
Out[25]=
In[26]:=
LUDecomposition[\!\(\* TagBox[ TagBox[ RowBox[{"(", "", GridBox[{ {"3", "1", "5"}, {"2", "4", "6"}, {"8", "7", "9"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]
Out[26]=

Version History

  • 1.0.0 – 19 September 2022

Source Metadata

  • Citation:
    • Edelman A., "The Complete Pivoting Conjecture for Gaussian Elimination Is False. "$Failed, vol. 2, no. 2, 58-61, 1992.
      Available from       https://math.mit.edu/~edelman/publications/complete_pivoting.pdf
    • Foster L.V., "The growth factor and efficiency of Gaussian elimination with rook pivoting. "Journal of Computational and Applied Mathematics, vol. 86, no. 1, 177-194, 1997.
      DOI: 10.1016/S0377-0427(97)00154-4
    • Higham N.J., Higham D.J., "Large Growth Factors in Gaussian Elimination with Pivoting. "SIAM Journal on Matrix Analysis and Applications, vol. 10, no. 2, 155-164, 1989.
      DOI: 10.1137/0610012
    • Poole G., Neal L., "The Rook's pivoting strategy. "Journal of Computational and Applied Mathematics, vol. 123, nos. 1-2, 353-369, 2000.
      DOI: 10.1016/S0377-0427(00)00406-4

Related Resources

License Information