Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the shortest displacement between two points in a box with periodic boundary conditions
ResourceFunction["PeriodicBoxDisplacement"][u,v,L] gives the shortest displacement between vectors u and v in a cubic box of side length L centered on the origin with periodic boundary conditions. |
Compute a 1D periodic box displacement in the "box" represented by the interval [-1,1]:
| In[1]:= |
| Out[1]= |
PeriodicBoxDisplacement reverts to Euclidean displacement when points are close by within the box:
| In[2]:= |
| Out[2]= |
Parallel points on the boundaries of the box are mapped to the same point:
| In[3]:= |
| Out[3]= |
PeriodicBoxDisplacement also works in higher dimensions:
| In[4]:= |
| Out[4]= |
Visualize the displacement vector between two points in different boxes (dashed boxes are "copies" of the main box due to periodic boundary conditions):
| In[5]:= | ![With[{u = {3, 4}, v = {-3, -4}, L = 10},
Graphics[{Table[{{
Directive[
FaceForm[],
EdgeForm[
If[{x, y} == {0, 0},
Directive[Thick,
Opacity[1], Black],
Directive[Gray, Dashed]]]],
Rectangle[{Rational[-1, 2] L - x, Rational[-1, 2] L - y}, {Rational[1, 2] L + x, Rational[1, 2] L + y}]},
{Blue, Disk[u + {x, y}]},
{Directive[Gray, Opacity[0.5]], Disk[v + {x, y}]}},
{x, {-L, 0, L}}, {y, {-L, 0, L}}],
Arrow[{u, u + ResourceFunction["PeriodicBoxDisplacement"][u, v, L]}]}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b9e/b9e10af0-136e-4267-a29b-445abc4d21f3/398be36698d56b41.png) |
| Out[5]= | 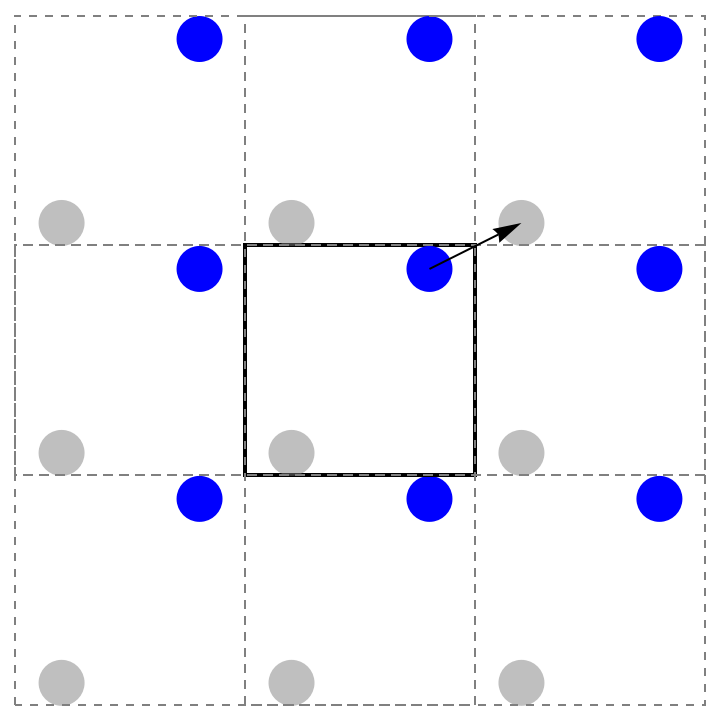 |
In three dimensions:
| In[6]:= | ![With[{u = {2, 3, 4}, v = {-2, -3, -4}, L = 10},
Graphics3D[{Table[{{
Directive[
FaceForm[],
EdgeForm[
If[{x, y, z} == {0, 0, 0},
Directive[Thick, Black],
Directive[Gray, Dashed]]]],
Cuboid[{Rational[-1, 2] L + x, Rational[-1, 2] L + y, Rational[-1, 2] L + z}, {Rational[1, 2] L + x, Rational[1, 2] L + y, Rational[1, 2] L + z}]},
{Blue, Sphere[u + {x, y, z}]},
{Gray, Sphere[v + {x, y, z}]}},
{x, {0, L}}, {y, {0, L}}, {z, {0, L}}],
{Red, Arrow[
Tube[{u, u + ResourceFunction["PeriodicBoxDisplacement"][u, v, L]}]]}},
Boxed -> False, Lighting -> "Accent"]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b9e/b9e10af0-136e-4267-a29b-445abc4d21f3/66dd543705fb72d7.png) |
| Out[6]= | 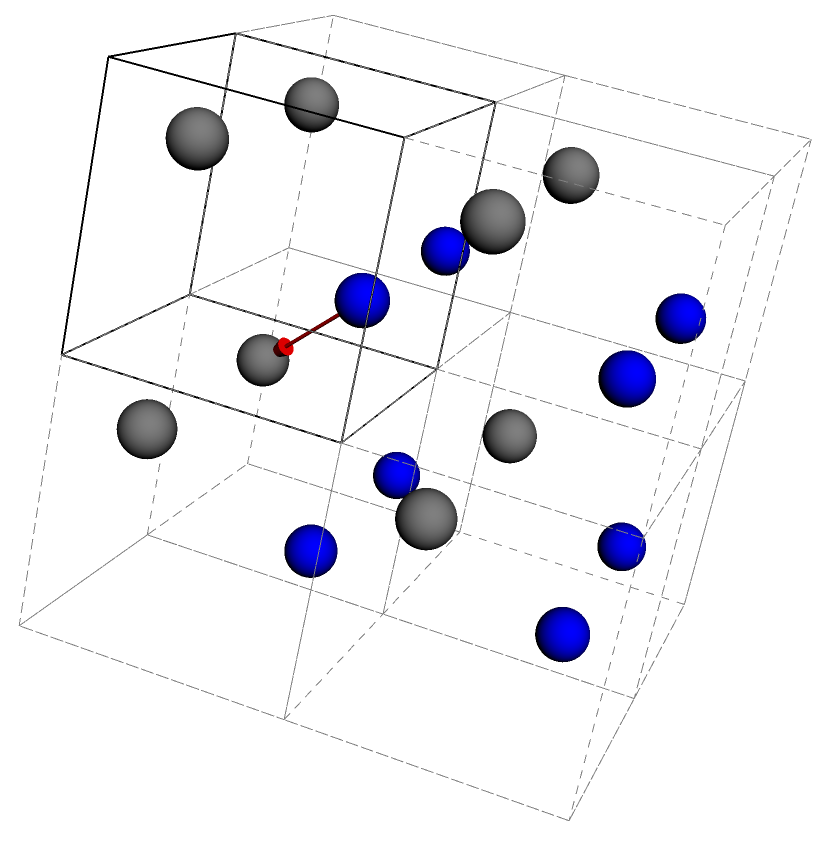 |
This work is licensed under a Creative Commons Attribution 4.0 International License