Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute a pedal surface
ResourceFunction["PedalSurface"][s,p,{u,v}] computes the pedal surface with respect to the point p of the surface s parameterized by variables {u,v}. |
Get the equation of an ellipsoid surface:
| In[1]:= |
| Out[1]= |
Compute the pedal surface of the ellipsoid:
| In[2]:= |
| Out[2]= |
Plot the pedal surface; it is a particular case of Fresnel’s elasticity surface:
| In[3]:= |
| Out[3]= | 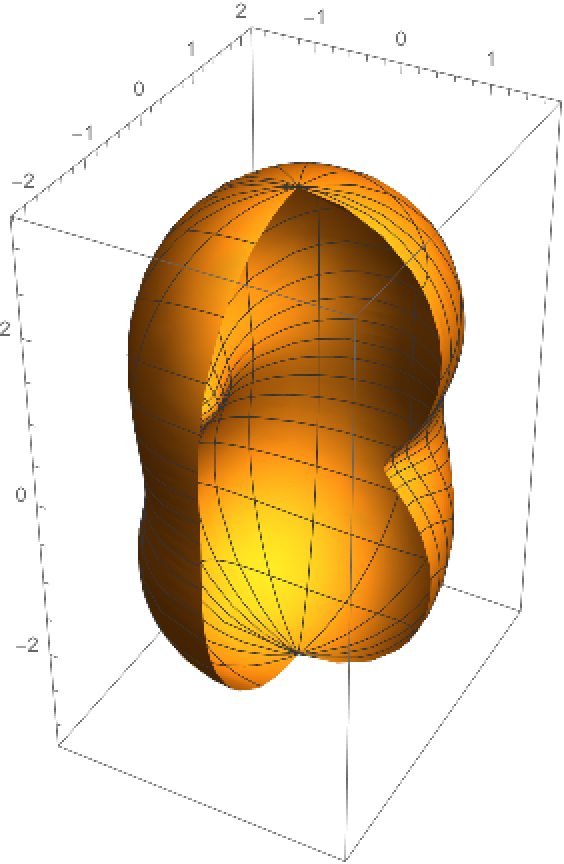 |
The following Manipulate shows how the pedal surface is constructed. Note that the tangent plane at a point of the ellipsoid is perpendicular to the red line:
| In[4]:= |
| In[5]:= | ![Manipulate[Evaluate[Show[surfaces, Graphics3D[
{InfinitePlane[
ellipsoid[u, v], {Derivative[1, 0][ellipsoid][u, v], Derivative[0, 1][ellipsoid][u, v]}], Red, Thickness[0.0035], Line[{{0, 0, 0}, ps}], Green, PointSize[0.03], Point[ps]}]]], {{u, 0.75}, 0, (3*Pi)/2}, {{v, 0.3}, 0, Pi}]](https://www.wolframcloud.com/obj/resourcesystem/images/31b/31be8c57-92ca-4830-abac-92ad38ade854/17b1504838f504a0.png) |
| Out[5]= | 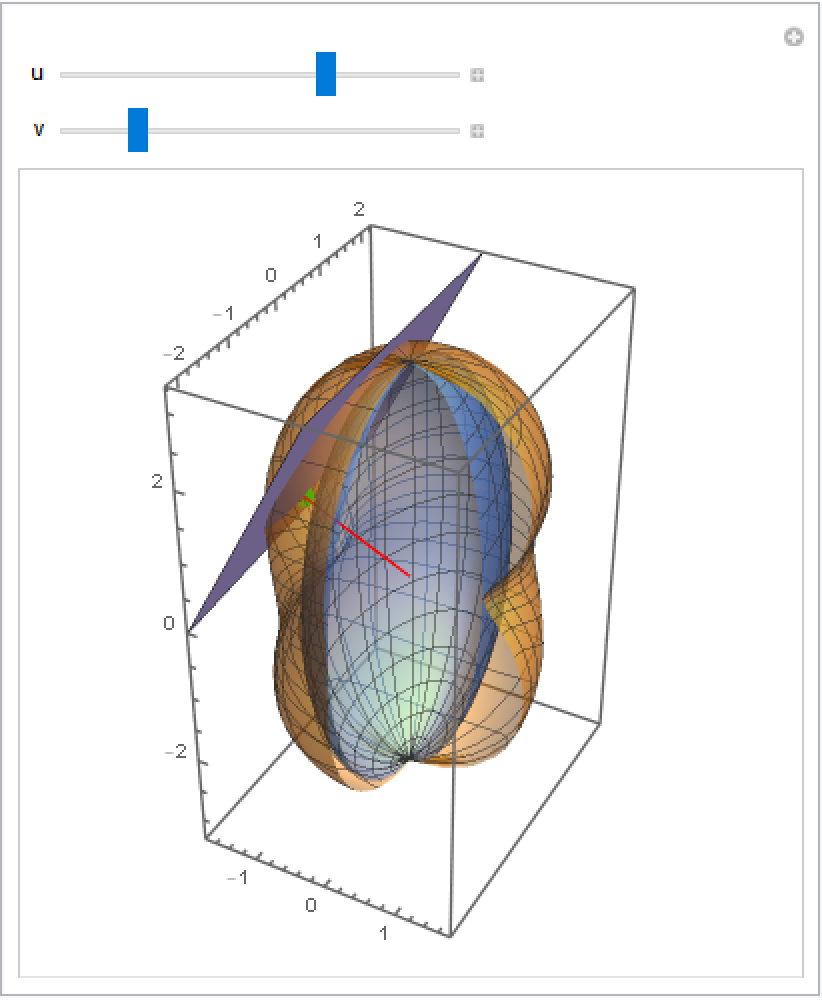 |
Get the equation for an ellipse:
| In[6]:= |
| Out[6]= |
Compute the pedal curve of the ellipse:
| In[7]:= |
| Out[7]= |
Plot the pedal curve; the contour is like the 3D case:
| In[8]:= |
| Out[8]= | 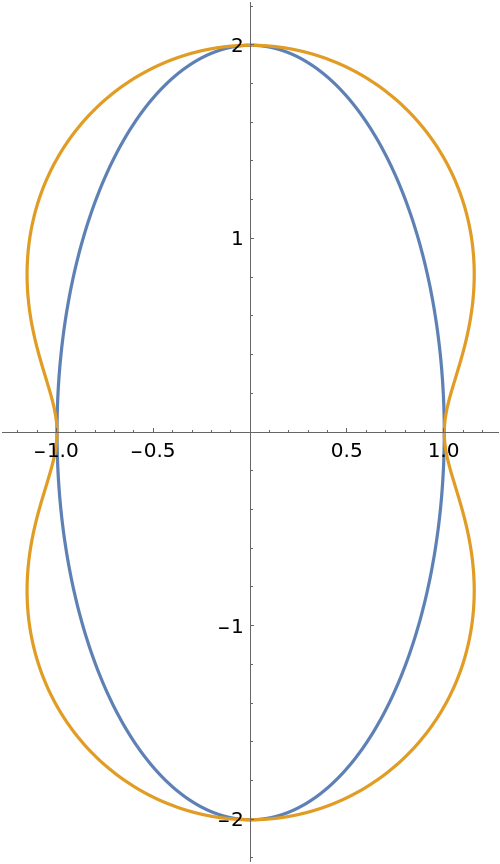 |
This work is licensed under a Creative Commons Attribution 4.0 International License