Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the pedal of a curve
ResourceFunction["PedalCurve"][c,t] computes the pedal curve of a curve c with parameter t. | |
ResourceFunction["PedalCurve"][c,p,t] computes the pedal curve from the point p with parameter t. |
Define a cardioid:
| In[1]:= |
| Out[1]= |
Compute the pedal curve of the cardioid:
| In[2]:= |
| Out[2]= |
Plot the cardioid (blue) along with its pedal curve (orange):
| In[3]:= |
| Out[3]= | 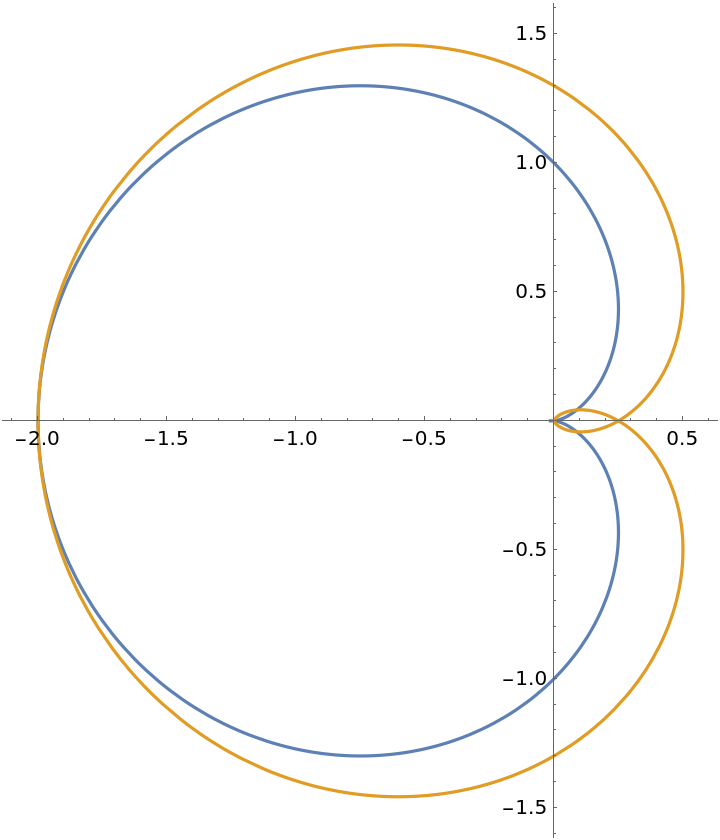 |
The pedal curve of an ellipse from different points:
| In[4]:= | ![GraphicsGrid[
Partition[
Table[ParametricPlot[
Evaluate[{{Sin[t], .5 Cos[t]}, ResourceFunction["PedalCurve"][{Sin[t], .5 Cos[t]}, p, t]}], {t,
0, 2 \[Pi]}, Epilog -> Point[p], Axes -> False], {p, {{.5, 0}, {1, 0}, {0, .25}, {0, 1}}}], 2]]](https://www.wolframcloud.com/obj/resourcesystem/images/773/773522c5-de3f-4a76-b8cb-46b60ffa2bf7/061d1132fbb11f16.png) |
| Out[4]= | 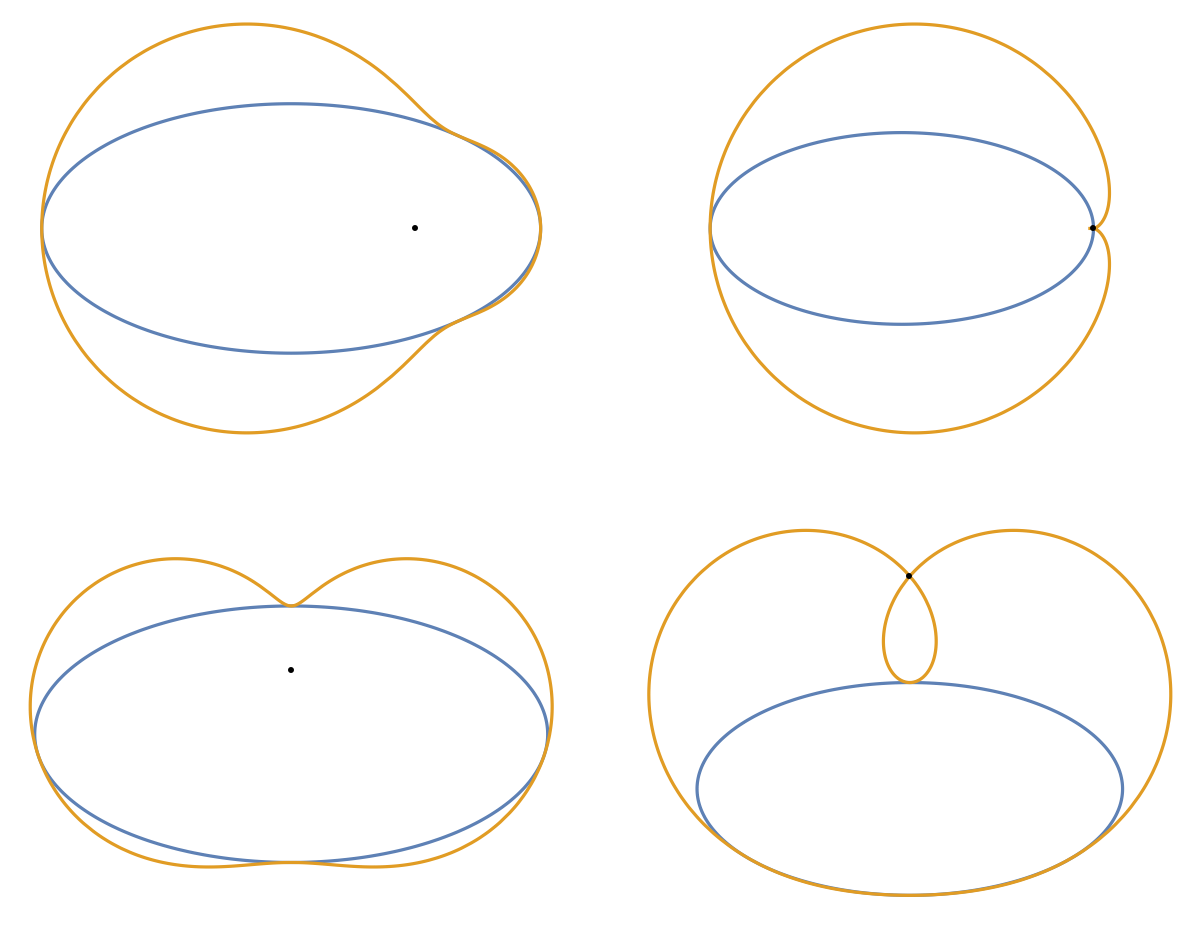 |
Nested pedal curves:
| In[5]:= |
| Out[5]= | 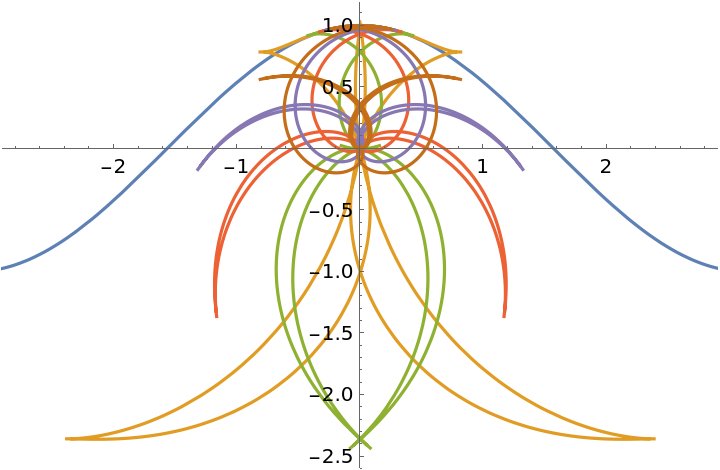 |
This work is licensed under a Creative Commons Attribution 4.0 International License