Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the tangent plane of a parametric surface
ResourceFunction["ParametricSurfaceTangentPlane"][s,{u,v},{u0,v0}] computes the tangent plane at the point (u0,v0) of surface s parametrized by variables u and v. |
Definition of a sphere:
| In[1]:= |
| Out[1]= |
Tangent plane of the sphere:
| In[2]:= | ![ResourceFunction["ParametricSurfaceTangentPlane"][
Entity["Surface", "Sphere"]["ParametricEquations"][1][u, v], {u, v}, {u0, v0}]](https://www.wolframcloud.com/obj/resourcesystem/images/cc3/cc378150-1b33-4fce-aca5-20be35284312/6548e653b8ac640a.png) |
| Out[2]= |
Plot the tangent plane at any point on a sphere:
| In[3]:= | ![Manipulate[
With[{p = {Cos[u0] Sin[v0], Sin[u0] Sin[v0], Cos[v0]}, p1 = {-(u - u0) Sin[u0] Sin[v0], (u - u0) Cos[u0] Sin[v0], 0}, p2 = {(v - v0) Cos[u0] Cos[v0], (v - v0) Cos[v0] Sin[
u0], -(v - v0) Sin[v0]}}, Graphics3D[{Opacity[.5], Sphere[], PointSize[.025], Point[Normalize[p1]/2 + p], Arrow[{p, Normalize[p1]/2 + p}], Point[Normalize[p2]/2 + p], Arrow[{p, Normalize[p2]/2 + p}], Red,
Point[p], Blue, Opacity[.25], ResourceFunction["ParametricSurfaceTangentPlane"][
Entity["Surface", "Sphere"]["ParametricEquations"][1][u, v], {u,
v}, {u0, v0}]} /. {u -> Cos[u0], v -> Sin[v0]}, Axes -> True]], {{u0, -1}, -\[Pi], \[Pi]}, {{v0, 1.}, -\[Pi], \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/cc3/cc378150-1b33-4fce-aca5-20be35284312/358bee4bbabc9331.png) |
| Out[3]= | 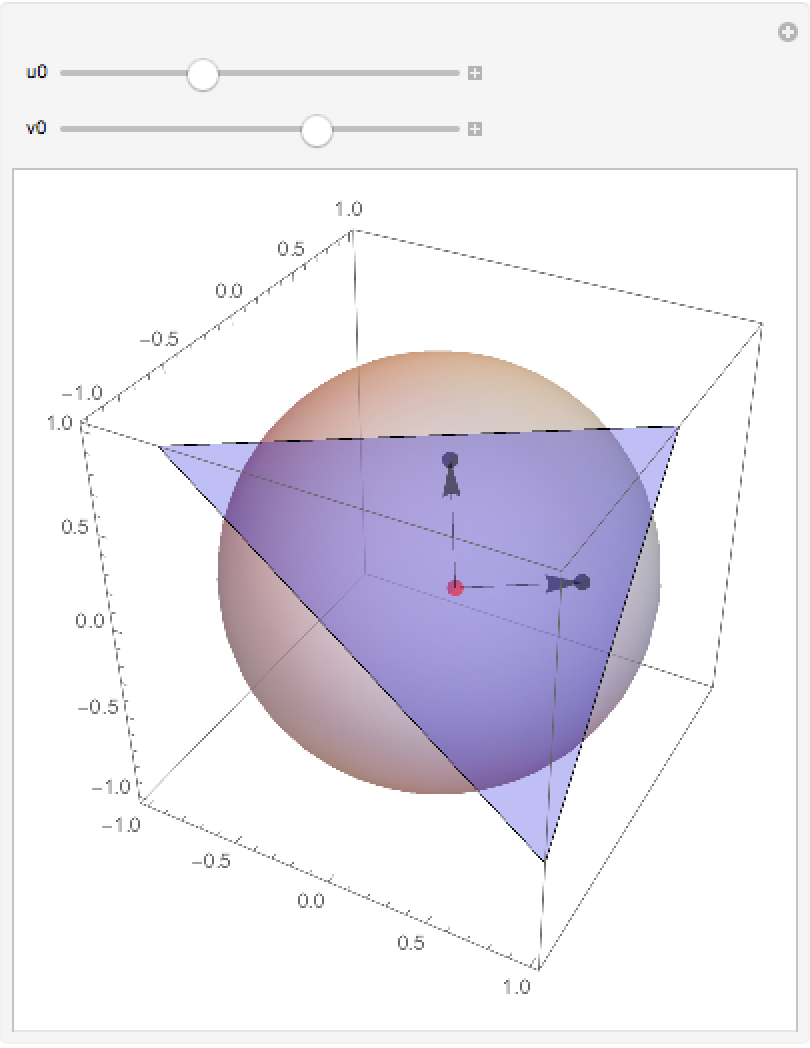 |
Choose a surface:
| In[4]:= |
| Out[4]= |
Plot it:
| In[5]:= | ![plot = ParametricPlot3D[
Evaluate[surf], {u, 0, 3 \[Pi]}, {v, 0, 3 \[Pi]}, Mesh -> False, PlotStyle -> Opacity[.75], PlotRange -> {{0, 3 \[Pi]}, {0, 3 \[Pi]}, {-1.1, 1.4}},
SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/cc3/cc378150-1b33-4fce-aca5-20be35284312/2f3bf071154bfe0a.png) |
| Out[5]= | 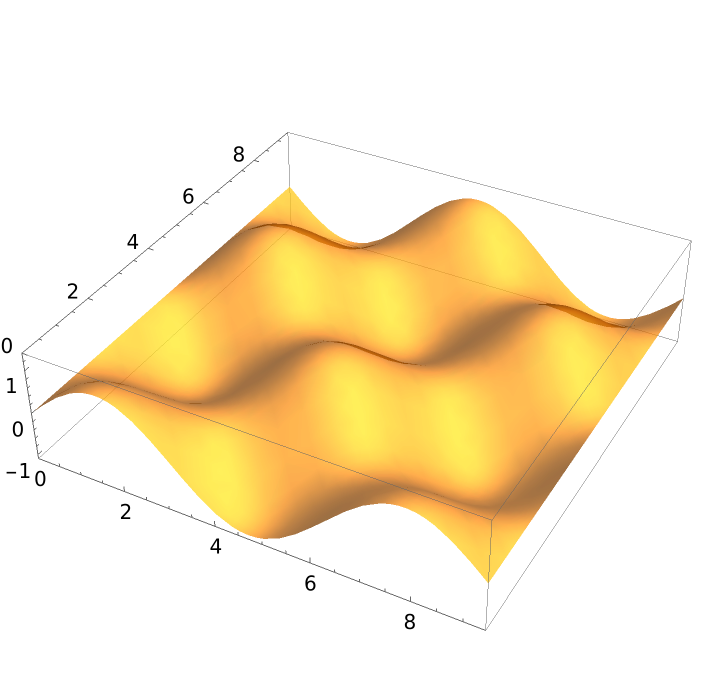 |
Compute the tangent plane of the surface:
| In[6]:= |
| Out[6]= |
Plot the tangent plane at any point (in blue) on the surface; the red curves are the intersection of the plane and the surface:
| In[7]:= | ![Manipulate[
Show[plot, Graphics3D[{Blue, Opacity[.5], ResourceFunction["ParametricSurfaceTangentPlane"][
surf, {u, v}, {u0, v0}] /. {u -> Cos[u0], v -> Sin[v0]}, Red, Thickness[.0075], Cases[Normal[
ContourPlot[
Cos[v] Sin[u] == Cos[v0] Sin[u0] + (u - u0) Cos[u0] Cos[v0] - (v - v0) Sin[
u0] Sin[v0], {u, 0, 3 \[Pi]}, {v, 0, 3 \[Pi]}]], _Line, \[Infinity]] /. {u_Real, v_Real} -> {u, v,
Sin[u] Cos[v]}, PointSize[.035], Green, Point[{u0, v0, Sin[u0] Cos[v0]}]}]], {{u0, 2.82}, 0, 3 \[Pi]}, {{v0, 4.43}, 0, 3 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/cc3/cc378150-1b33-4fce-aca5-20be35284312/7c4e67ccd8ece480.png) |
| Out[7]= | 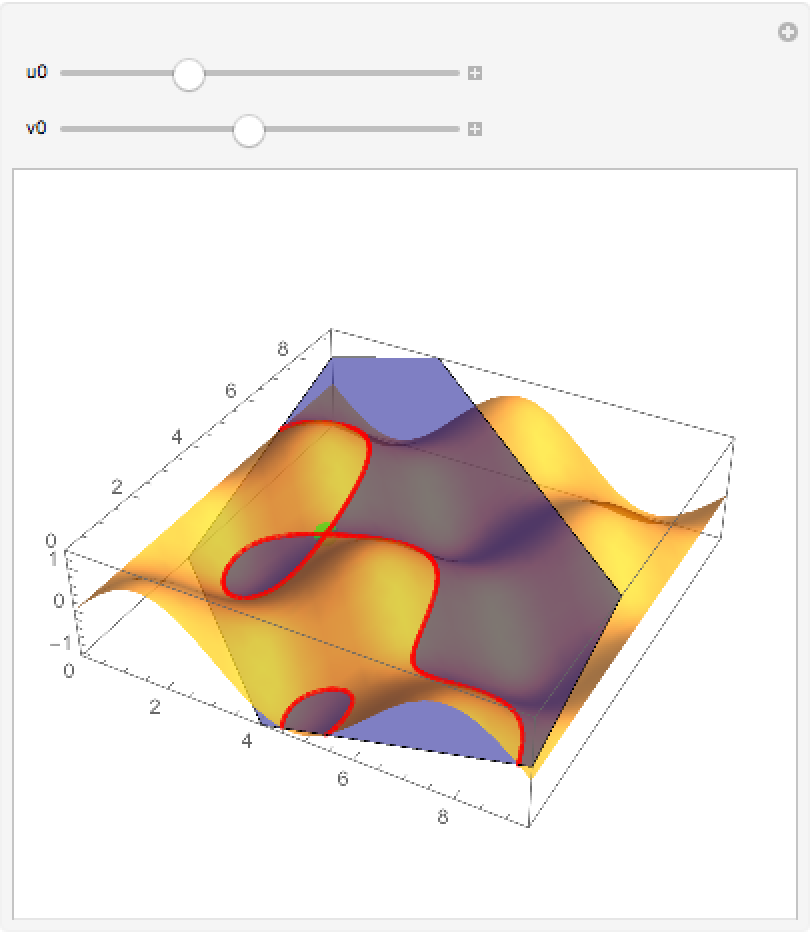 |
Use ClipPlanes to view the surface only at one side of the plane:
| In[8]:= | ![Manipulate[
Show[ParametricPlot3D[
Evaluate[surf], {u, 0, 3 \[Pi]}, {v, 0, 3 \[Pi]}, PlotStyle -> Opacity[.75], ClipPlanes -> (ResourceFunction["ParametricSurfaceTangentPlane"][
surf, {u, v}, {u0, v0}] /. {u -> Cos[u0], v -> Sin[v0]}), ClipPlanesStyle -> Directive[Opacity[.5], Blue], Mesh -> False, PlotRange -> {{0, 3 \[Pi]}, {0, 3 \[Pi]}, {-1.1, 1.4}}], Graphics3D[{PointSize[.035], Green, Point[{u0, v0, Sin[u0] Cos[v0]}]}]], {{u0, 2.82}, 0, 3 \[Pi]}, {{v0, 4.43}, 0, 3 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/cc3/cc378150-1b33-4fce-aca5-20be35284312/5ad9c517bf6dbdf4.png) |
| Out[8]= | 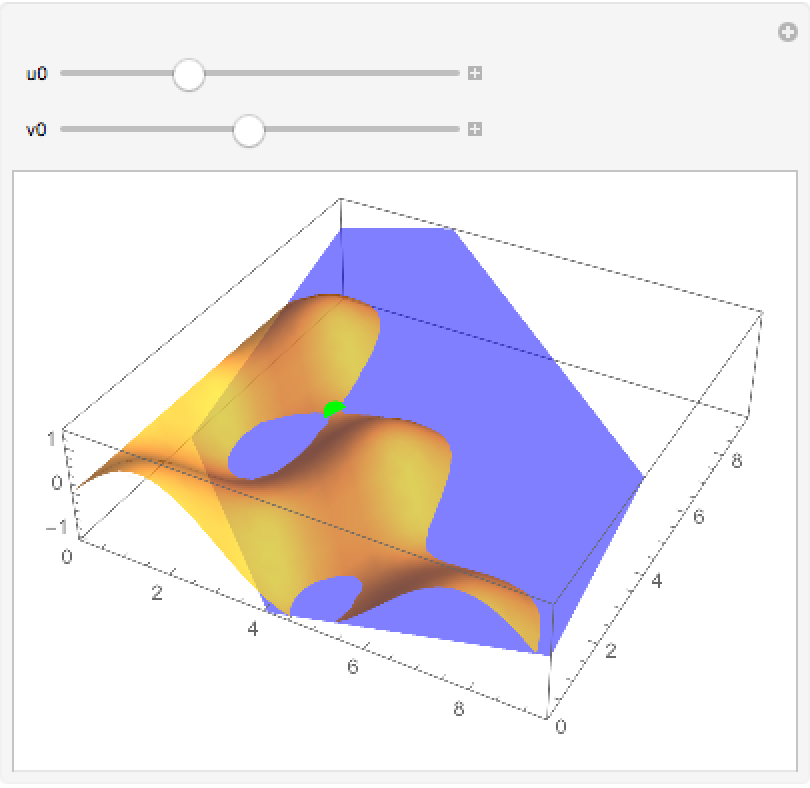 |
This work is licensed under a Creative Commons Attribution 4.0 International License