Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the orthogonal polynomial Vandermonde matrix corresponding to a given vector
ResourceFunction["OrthogonalPolynomialVandermondeMatrix"][poly,{a1,a2,…}] generates the orthogonal polynomial Vandermonde matrix V(a1,a2,…) with respect to the basis represented by poly. |
| "ChebyshevFirst" | Chebyshev polynomial of the first kind ChebyshevT[i,x] |
| "ChebyshevSecond" | Chebyshev polynomial of the second kind ChebyshevU[i,x] |
| "Hermite" | Hermite polynomial HermiteH[i,x] |
| "Laguerre" | Laguerre polynomial LaguerreL[i,x] |
| "Legendre" | Legendre polynomial LegendreP[i,x] |
| {"Gegenbauer",m} | Gegenbauer polynomial GegenbauerC[i,m,x] |
| {"Laguerre",a} | associated Laguerre polynomial LaguerreL[i,a,x] |
| {"Jacobi",a,b} | Jacobi polynomial JacobiP[i,a,b,x] |
A Chebyshev–Vandermonde matrix:
| In[1]:= |
|
| Out[1]= |
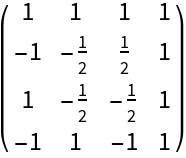
|
Jacobi–Vandermonde matrix with symbolic parameters and vector:
| In[2]:= |
|
| Out[2]= |
|
An equivalent specification:
| In[3]:= |
|
| Out[3]= |
|
A numerical Hermite–Vandermonde matrix:
| In[4]:= |
|
| Out[4]= |

|
A rectangular Legendre–Vandermonde matrix:
| In[5]:= |
|
| Out[5]= |
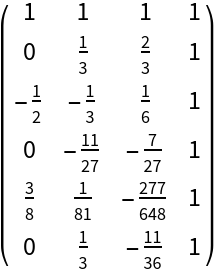
|
With "Transpose"→True, OrthogonalPolynomialVandermondeMatrix generates a transposed matrix:
| In[6]:= |
![MatrixForm /@ {ResourceFunction[
"OrthogonalPolynomialVandermondeMatrix"]["Laguerre", {x1, x2, x3}, "Transpose" -> False], ResourceFunction["OrthogonalPolynomialVandermondeMatrix"][
"Laguerre", {x1, x2, x3}, "Transpose" -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/326/326b0428-2049-4d11-b87b-240edd4921f2/7a66cd48d66035a3.png)
|
| Out[6]= |
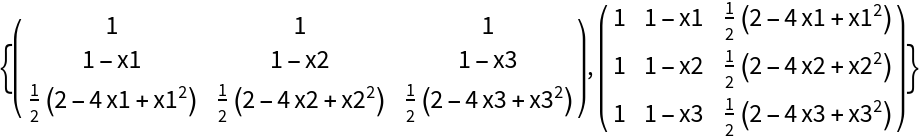
|
| In[7]:= |
![MatrixForm /@ {ResourceFunction[
"OrthogonalPolynomialVandermondeMatrix"]["Laguerre", 4, {x1, x2, x3}, "Transpose" -> False], ResourceFunction["OrthogonalPolynomialVandermondeMatrix"][
"Laguerre", 4, {x1, x2, x3}, "Transpose" -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/326/326b0428-2049-4d11-b87b-240edd4921f2/69a8bb4c2d3bcbc6.png)
|
| Out[7]= |
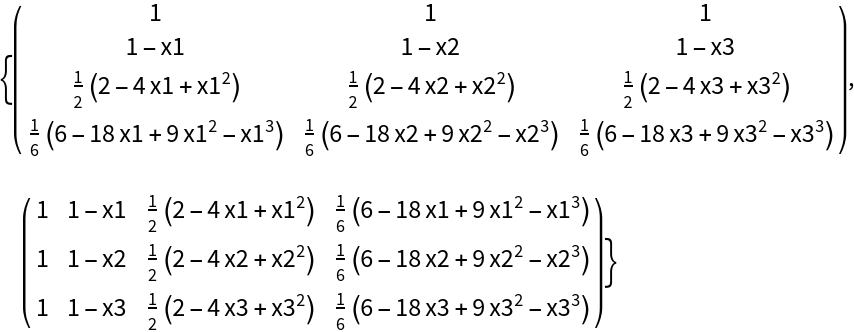
|
This work is licensed under a Creative Commons Attribution 4.0 International License