Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 OrthogonalPolynomialDividedDifference

Source Notebook

Evaluate the divided difference of a finite orthogonal polynomial series

Contributed by: Jan Mangaldan

ResourceFunction["OrthogonalPolynomialDividedDifference"][cof,poly,x,y]

evaluates the divided difference , where ci is the (i+1)th element of the list cof.

Details

The argument poly can be any of the following:
"ChebyshevFirst"Chebyshev polynomial of the first kind ChebyshevT[i,x]
"ChebyshevSecond"Chebyshev polynomial of the second kind ChebyshevU[i,x]
"Hermite"Hermite polynomial HermiteH[i,x]
"Laguerre"Laguerre polynomial LaguerreL[i,x]
"Legendre"Legendre polynomial LegendreP[i,x]
{"Gegenbauer",m}Gegenbauer polynomial GegenbauerC[i,m,x]
{"Laguerre",a}associated Laguerre polynomial LaguerreL[i,a,x]
{"Jacobi",a,b}Jacobi polynomial JacobiP[i,a,b,x]
Strings in specifications like "Legendre" and {"Jacobi",a,b} can be replaced with the corresponding symbols, as in LegendreP and {JacobiP,a,b}.

Examples

Basic Examples (2) 

Divided difference of a Laguerre series:

In[1]:=
ResourceFunction[ "OrthogonalPolynomialDividedDifference"][{1/2, -1/4, 1/8, -1/16}, "Laguerre", 4/3, 1]
Out[1]=

Compare with an explicit evaluation using the resource function OrthogonalPolynomialSum:

In[2]:=
With[{c = {1/2, -1/4, 1/8, -1/16}, x = 4/3, y = 1}, (ResourceFunction["OrthogonalPolynomialSum"][c, "Laguerre", x] - ResourceFunction["OrthogonalPolynomialSum"][c, "Laguerre", y])/(x - y)]
Out[2]=

Scope (2) 

Divided difference of a Jacobi series with symbolic coefficients, parameters and arguments:

In[3]:=
ResourceFunction["OrthogonalPolynomialDividedDifference"][ Array[C, 3, 0], {"Jacobi", \[Alpha], \[Beta]}, x, y]
Out[3]=

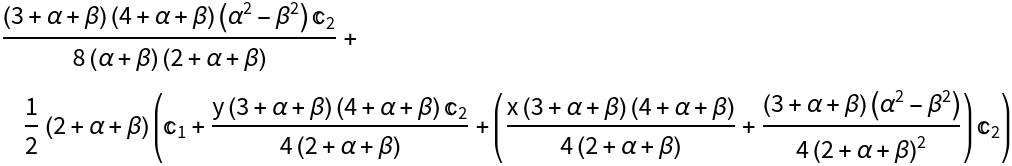
An equivalent specification:

In[4]:=
ResourceFunction["OrthogonalPolynomialDividedDifference"][ Array[C, 3, 0], {JacobiP, \[Alpha], \[Beta]}, x, y]
Out[4]=

Applications (2) 

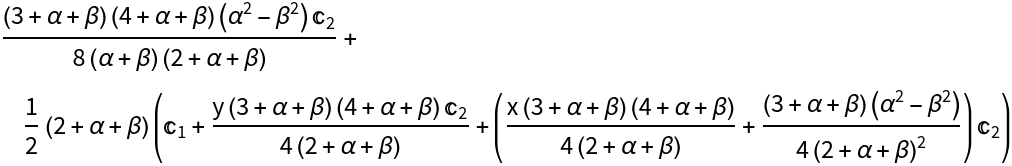
Directly evaluating the divided difference using the resource function OrthogonalPolynomialSum gives a result that is not very accurate:

In[5]:=
With[{c = {1/2, -1/4, 1/8, -1/16}, \[CurlyEpsilon] = N[3*^-8, 20]}, (ResourceFunction["OrthogonalPolynomialSum"][ c, {"Laguerre", -1/2}, 5 + \[CurlyEpsilon]] - ResourceFunction["OrthogonalPolynomialSum"][c, {"Laguerre", -1/2}, 5 - \[CurlyEpsilon]])/((5 + \[CurlyEpsilon]) - (5 - \ \[CurlyEpsilon]))]
Out[5]=

OrthogonalPolynomialDividedDifference gives a more accurate result:

In[6]:=
With[{c = {1/2, -1/4, 1/8, -1/16}, \[CurlyEpsilon] = N[3*^-8, 20]}, ResourceFunction["OrthogonalPolynomialDividedDifference"][ c, {"Laguerre", -1/2}, 5 - \[CurlyEpsilon], 5 + \[CurlyEpsilon]]]
Out[6]=

Evaluate the q-derivative of a Chebyshev series:

In[7]:=
ResourceFunction[ "OrthogonalPolynomialDividedDifference"][{1, -1/3, 1/5, -1/7, 1/11}, ChebyshevT, x, q x]
Out[7]=

In the limit q→1, the q-derivative reduces to the derivative:

In[8]:=
Limit[%, q -> 1]
Out[8]=
In[9]:=
% == D[ResourceFunction["OrthogonalPolynomialSum"][{1, -1/3, 1/5, -1/7, 1/11}, ChebyshevT, x], x] // Simplify
Out[9]=

Properties and Relations (2) 

OrthogonalPolynomialDividedDifference is symmetric in the arguments x and y:

In[10]:=
ResourceFunction["OrthogonalPolynomialDividedDifference"][ Array[C, 4, 0], "Legendre", x, y] == ResourceFunction["OrthogonalPolynomialDividedDifference"][ Array[C, 4, 0], "Legendre", y, x] // Simplify
Out[10]=

If x=y, the result of OrthogonalPolynomialDividedDifference is equal to the derivative of the orthogonal polynomial series, evaluated at x:

In[11]:=
ResourceFunction["OrthogonalPolynomialDividedDifference"][ Array[C, 4, 0], "Legendre", x, x] == (D[ ResourceFunction["OrthogonalPolynomialSum"][Array[C, 4, 0], "Legendre", t], t] /. t -> x) // Simplify
Out[11]=

Version History

  • 1.0.0 – 06 April 2021

Source Metadata

  • Citation:
    • Hunter D.B., Clenshaw’s method for evaluating certain finite series. Computer Journal, vol. 13, no. 4, 378-381, 1970.
      DOI: 10.1093/comjnl/13.4.378

Related Resources

License Information