Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 OrthogonalPolynomialSum

Source Notebook

Evaluate a finite orthogonal polynomial series

Contributed by: Jan Mangaldan

ResourceFunction["OrthogonalPolynomialSum"][f,poly,x,{i,imin,imax}]

evaluates the sum , where pi(x) is an orthogonal polynomial represented by poly.

ResourceFunction["OrthogonalPolynomialSum"][cof,poly,x]

evaluates the sum , where ci is the (i+1)th element of the list cof.

Details

The argument poly can be any of the following:
"ChebyshevFirst"Chebyshev polynomial of the first kind ChebyshevT[i,x]
"ChebyshevSecond"Chebyshev polynomial of the second kind ChebyshevU[i,x]
"Hermite"Hermite polynomial HermiteH[i,x]
"Laguerre"Laguerre polynomial LaguerreL[i,x]
"Legendre"Legendre polynomial LegendreP[i,x]
{"Gegenbauer",m}Gegenbauer polynomial GegenbauerC[i,m,x]
{"Laguerre",a}associated Laguerre polynomial LaguerreL[i,a,x]
{"Jacobi",a,b}Jacobi polynomial JacobiP[i,a,b,x]
Strings in specifications like "Legendre" and {"Jacobi",a,b} can be replaced with the corresponding symbols, as in LegendreP and {JacobiP,a,b}.
ResourceFunction["OrthogonalPolynomialSum"] uses Clenshaw summation to evaluate the sum.

Examples

Basic Examples (2) 

Evaluate a finite Laguerre sum:

In[1]:=
ResourceFunction["OrthogonalPolynomialSum"][1/( k + 1), "Laguerre", 3/2, {k, 0, 5}]
Out[1]=

Compare with the result of Sum:

In[2]:=
\!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(5\)]\( \*FractionBox[\(1\), \(k + 1\)] LaguerreL[k, \*FractionBox[\(3\), \(2\)]]\)\)
Out[2]=

Scope (3) 

Evaluate a finite Jacobi sum with symbolic coefficients and parameters:

In[3]:=
ResourceFunction["OrthogonalPolynomialSum"][ C[k], {JacobiP, \[Alpha], \[Beta]}, x, {k, 0, 3}]
Out[3]=

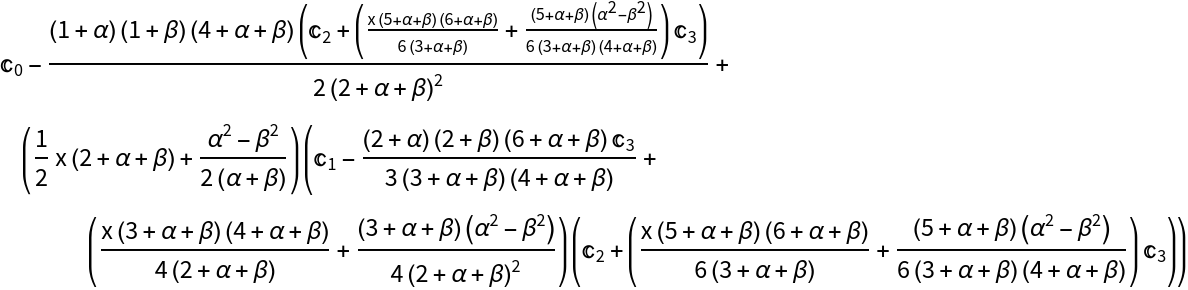
Compare with an explicit summation:

In[4]:=
% == \!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(3\)]\(C[k] JacobiP[ k, \[Alpha], \[Beta], x]\)\) // Simplify
Out[4]=

Evaluate a partial sum of a Gegenbauer series:

In[5]:=
ResourceFunction["OrthogonalPolynomialSum"][k, {"Gegenbauer", 3/2}, 3/4, {k, 3, 5}]
Out[5]=

Compare with an explicit summation:

In[6]:=
\!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 3\), \(5\)]\(k\ GegenbauerC[k, 3/2, 3/4]\)\) // Simplify
Out[6]=

Evaluate a finite Hermite sum with coefficients supplied from a list:

In[7]:=
ResourceFunction[ "OrthogonalPolynomialSum"][{1/2, -1/4, 1/8, -1/16}, "Hermite", 1/6]
Out[7]=

Compare with an explicit evaluation:

In[8]:=
{1/2, -1/4, 1/8, -1/16} . HermiteH[Range[0, 3], 1/6]
Out[8]=

Properties and Relations (3) 

Generate random coefficients of a Legendre series:

In[9]:=
c1 = RandomVariate[NormalDistribution[], 35, WorkingPrecision -> 25];

Evaluating the Legendre series with OrthogonalPolynomialSum is faster than using LegendreP:

In[10]:=
AbsoluteTiming[ r1 = ResourceFunction["OrthogonalPolynomialSum"][N[c1], "Legendre", 1.1]]
Out[10]=
In[11]:=
AbsoluteTiming[r2 = N[c1] . LegendreP[Range[0, Length[c1] - 1], 1.1]]
Out[11]=

The result obtained through OrthogonalPolynomialSum also has a slightly smaller error:

In[12]:=
trueRes = c1 . LegendreP[Range[0, Length[c1] - 1], 11/10]
Out[12]=
In[13]:=
r1 - trueRes
Out[13]=
In[14]:=
r2 - trueRes
Out[14]=

Version History

  • 1.0.0 – 05 April 2021

Source Metadata

  • Citation:
    • Clenshaw C.W., A note on the summation of Chebyshev series. Mathematical Tables and Other Aids to Computation, vol. 9, 118-120, 1955.
      DOI: 10.1090/S0025-5718-1955-0071856-0
    • Smith F.J., An algorithm for summing orthogonal polynomial series and their derivatives with applications to curve-fitting and interpolation. Mathematics of Computation, vol. 19, 33-36, 1965.
      DOI: 10.1090/S0025-5718-1965-0172445-6

Related Resources

License Information