Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NetworkXObject

Source Notebook

Use graph algorithms from the Python package NetworkX without any Python programming

Contributed by: Igor Bakshee, with examples adapted from the NetworkX documentation

ResourceFunction["NetworkXObject"][]

returns a configured PythonObject for the Python package NetworkX in a new Python session.

ResourceFunction["NetworkXObject"][session]

uses the specified running ExternalSessionObject session.

ResourceFunction["NetworkXObject"][…,"func"[args,opts]]

executes the function func with the specified arguments and options.

Details and Options

NetworkX is a Python package for the creation, manipulation, and study of the structure, dynamics and functions of complex networks.
ResourceFunction["NetworkXObject"] sets up a configuration of the resource function PythonObject that makes working with NetworkX more convenient.
ResourceFunction["NetworkXObject"] exports Wolfram Language Graph objects to Python, imports Python graphs and makes the Python-side functions and properties accessible by new names that are closer to the usual Wolfram Language conventions.
For a Python object p, p["ToPythonName","wlname"] gives the name of the native Python name corresponding to the Wolfram Language name wlname and p["FromPythonName","pname"] gives the respective Wolfram Language name for the Python-side name pname. In the object p, both wlname and pname can be used interchangeably.
p["RenamingRules"] gives a list of all renaming rules in the form {"wlname1"→"pname1",…}.
p["FullInformation","Functions"] gives a list of the available functions and p["Information","func"] gives the signature of the specified function.
p["WebInformation"] gives a link to the NetworkX documentation that can be opened with SystemOpen.
Typically, the Wolfram Language signature of a NetworkX function closely resembles the Python-side signature in which Python-side objects are represented in the form of the resource function PythonObject with possible extensions suitable for the Wolfram Language.
When constructing graphs from the Graph object, ResourceFunction["NetworkXObject"] utilizes vertex IDs returned by VertexList. Use the function RelabelNodes to assign a different set of IDs.
NetworkXObject interoperates with the resource function MatplotlibObject to draw graphs on the Python side in cases when bringing data to the Wolfram Language for plotting is undesirable or impractical.
For sparse matrices, ResourceFunction["NetworkXObject"] automatically sets up Python object configuration using the resource function SciPyObject.
ResourceFunction["NetworkXObject"][session,"Explore"[category,patt]] gives a browsable table of contents of the module matching patt in the given category. category can be "Functions" or "Classes". patt can be derived from nx["FullInformation","Modules"].
ResourceFunction["NetworkXObject"][session,"Explore"[category,patt,"ColumnHeadings"→{"name1",…}]] uses the specified column headings.

Examples

Basic Examples (2) 

Create a NetworkX object:

In[1]:=
nx = ResourceFunction["NetworkXObject"][]
Out[1]=

Construct an undirected graph from an edge list:

In[2]:=
edges = {1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1};
In[3]:=
nx["Graph"[edges]]
Out[3]=

Import the Python object as a Graph:

In[4]:=
Normal[%]
Out[4]=

The imported graph is a standard Wolfram Language object:

In[5]:=
UndirectedGraphQ[%]
Out[5]=
In[6]:=
Graph[%%, VertexLabels -> Automatic]
Out[6]=

Get a directed graph:

In[7]:=
nx["DiGraph"[edges]]
Out[7]=
In[8]:=
Normal[%]
Out[8]=
In[9]:=
DirectedGraphQ[%]
Out[9]=

Clean up the Python session:

In[10]:=
DeleteObject[nx["Session"]]

An undirected graph supporting multiple edges between vertices:

In[11]:=
nx = ResourceFunction["NetworkXObject"][]
Out[11]=
In[12]:=
edges = {1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3};
In[13]:=
g = nx["MultiGraph"[edges]]
Out[13]=
In[14]:=
Normal[%]
Out[14]=
In[15]:=
MultigraphQ[%]
Out[15]=

A directed multigraph:

In[16]:=
nx["MultiDiGraph"[edges]]
Out[16]=
In[17]:=
Normal[%]
Out[17]=
In[18]:=
{MultigraphQ[%], DirectedGraphQ[%]}
Out[18]=
In[19]:=
DeleteObject[nx["Session"]]

Scope (58) 

Nodes and Edges (15) 

Create an empty graph:

In[20]:=
nx = ResourceFunction["NetworkXObject"][]
Out[20]=
In[21]:=
g = nx["Graph"[]]
Out[21]=

Nodes and edges of the graph are given as continuously updated NodeView and EdgeView objects:

In[22]:=
{g["Nodes"], g["Edges"]}
Out[22]=
In[23]:=
Normal /@ %
Out[23]=

Add one node at a time:

In[24]:=
g["AddNode"[1]]

Examine nodes:

In[25]:=
nodes = g["Nodes"]
Out[25]=
In[26]:=
Normal[%]
Out[26]=

Remove a node:

In[27]:=
g["RemoveNode"[1]]
In[28]:=
nodes // Normal
Out[28]=

Add nodes from a list:

In[29]:=
g["AddNodesFrom"[{2, 3, 4}]]
In[30]:=
nodes // Normal
Out[30]=

Remove several nodes:

In[31]:=
g["RemoveNodesFrom"[{2, 3}]]
In[32]:=
nodes // Normal
Out[32]=
In[33]:=
DeleteObject[nx["Session"]]
In[34]:=
nx = ResourceFunction["NetworkXObject"][]
Out[34]=
In[35]:=
g = nx["Graph"[]]
Out[35]=

Add nodes along with node attributes specified as an Association:

In[36]:=
g["AddNodesFrom"[{1, {2, <|"weight" -> 5|>}, {3, <| "color" -> "red"|>}, {4, <|"foo" -> "bar"|>}}]]
In[37]:=
(nodes = g["Nodes"]) // Normal
Out[37]=

Retrieve the specified node attribute:

In[38]:=
nx["GetNodeAttributes"[g, "color"]]
Out[38]=

Check the attributes of the imported graph:

In[39]:=
Normal[g]
Out[39]=
In[40]:=
Options[%, AnnotationRules]
Out[40]=
In[41]:=
AnnotationValue[%%, VertexWeight]
Out[41]=
In[42]:=
DeleteObject[nx["Session"]]

Create a new graph:

In[43]:=
nx = ResourceFunction["NetworkXObject"][]
Out[43]=
In[44]:=
g = nx["Graph"[]]
Out[44]=

To add a node attribute after a node is created, get a reference to the Python dictionary of node attributes:

In[45]:=
g["AddNode"[1]]
In[46]:=
g["Nodes"]["Part"[1], True]
Out[46]=

Adding a key→value pair to the dictionary adds an attribute to the graph:

In[47]:=
%["Assign"["Part"["room"] -> 714]]
Out[47]=
In[48]:=
g["Nodes"] // Normal
Out[48]=
In[49]:=
DeleteObject[nx["Session"]]

Create a new graph:

In[50]:=
nx = ResourceFunction["NetworkXObject"][]
Out[50]=
In[51]:=
g = nx["Graph"[]]
Out[51]=

Grow the graph by adding one edge at a time:

In[52]:=
g["AddEdge"[1, 2]]
In[53]:=
(edges = g["Edges"]) // Normal
Out[53]=

Add a list of edges:

In[54]:=
g["AddEdgesFrom"[{{1, 5}, {2, 3}, {2, 4}}]]

Add a list of edges with attributes:

In[55]:=
g["AddEdgesFrom"[{{1, 6}, {2, 5, <|"weight" -> 3|>}, {2, 4, <|"color" -> "red"|>}}]]
In[56]:=
edges // Normal
Out[56]=

Check the attributes in the imported graph:

In[57]:=
g // Normal
Out[57]=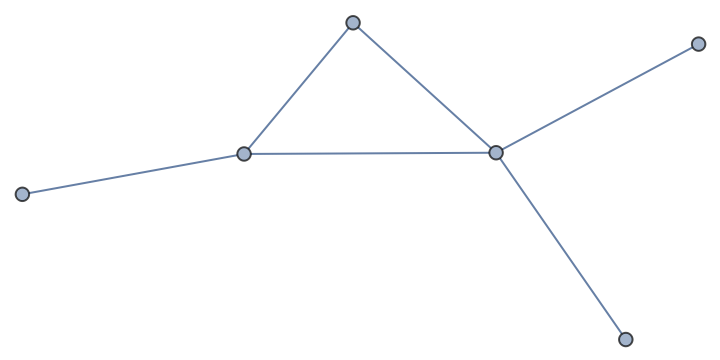
In[58]:=
Options[%, AnnotationRules]
Out[58]=
In[59]:=
AnnotationValue[%%, EdgeWeight]
Out[59]=

To add an edge attribute after an edge is created, assign a key→value pair to the dictionary of edge attributes:

In[60]:=
g["Part"[1, 2], True]
Out[60]=
In[61]:=
%["Assign"["Part"["weight"] -> 2]]
Out[61]=

Confirm the assignment for the edge 12:

In[62]:=
edges // Normal
Out[62]=

Remove a single edge:

In[63]:=
g["RemoveEdge"[1, 2]]
In[64]:=
edges // Normal
Out[64]=

Remove several edges:

In[65]:=
g["RemoveEdgesFrom"[{{2, 5}, {2, 4}}]]
In[66]:=
edges // Normal
Out[66]=
In[67]:=
DeleteObject[nx["Session"]]

Create a new empty graph:

In[68]:=
nx = ResourceFunction["NetworkXObject"][]
Out[68]=

Incorporate nodes from one graph into another:

In[69]:=
(g = nx["Graph"[{{1, 2}, {1, 3}, {1, 4}}]]) // Normal
Out[69]=
In[70]:=
(h = nx["PathGraph"[10]]) // Normal
Out[70]=
In[71]:=
g["AddNodesFrom"[h]]
In[72]:=
g["Nodes"] // Normal
Out[72]=
In[73]:=
g // Normal
Out[73]=
In[74]:=
DeleteObject[nx["Session"]]

Create a new empty graph:

In[75]:=
nx = ResourceFunction["NetworkXObject"][]
Out[75]=

Use one graph as a node in another:

In[76]:=
g = nx["Graph"[{{1, 2}}]]
Out[76]=
In[77]:=
(h = nx["PathGraph"[5]]) // Normal
Out[77]=
In[78]:=
g["AddNode"[h]]
In[79]:=
g["Nodes"] // Normal
Out[79]=
In[80]:=
Graph[g // Normal, VertexLabels -> Automatic]
Out[80]=
In[81]:=
DeleteObject[nx["Session"]]

Create a new empty graph:

In[82]:=
nx = ResourceFunction["NetworkXObject"][]
Out[82]=
In[83]:=
g = nx["Graph"[{{1, 2}, {1, 3}}]]
Out[83]=

Add a node "spam":

In[84]:=
g["AddNode"["spam"]]

Add four nodes "s", "p", "a", "m":

In[85]:=
g["AddNodesFrom"["spam"]]
In[86]:=
g["Nodes"] // Normal
Out[86]=
In[87]:=
DeleteObject[nx["Session"]]

Create a new empty graph:

In[88]:=
nx = ResourceFunction["NetworkXObject"][]
Out[88]=
In[89]:=
g = nx["Graph"[]]
Out[89]=

Incorporate edges from one graph into another:

In[90]:=
(g = nx["Graph"[{{1, 2}, {1, 3}, {1, 4}}]]) // Normal
Out[90]=
In[91]:=
(h = nx["PathGraph"[10]]) // Normal
Out[91]=
In[92]:=
g["AddEdgesFrom"[h["Edges"]]]
In[93]:=
g["Edges"] // Normal
Out[93]=
In[94]:=
g // Normal
Out[94]=
In[95]:=
DeleteObject[nx["Session"]]

Create a new multi-digraph graph:

In[96]:=
nx = ResourceFunction["NetworkXObject"][]
Out[96]=
In[97]:=
g = nx["MultiDiGraph"[]]
Out[97]=

Add edges with weights:

In[98]:=
g["AddWeightedEdgesFrom"[{{0, 1, 3.0}, {1, 2, 7.5}}]]
In[99]:=
g // Normal
Out[99]=
In[100]:=
g["Edges"] // Normal
Out[100]=
In[101]:=
DeleteObject[nx["Session"]]

Create a new multi-digraph:

In[102]:=
nx = ResourceFunction["NetworkXObject"][]
Out[102]=

Count nodes and edges in a graph:

In[103]:=
g = nx["MultiDiGraph"[{{2, 1}, {2, 1}, {2, 4}, {1, 3}, {1, 2}}]]
Out[103]=
In[104]:=
g // Normal
Out[104]=
In[105]:=
g["NumberOfNodes"[]]
Out[105]=
In[106]:=
g["NumberOfEdges"[]]
Out[106]=
In[107]:=
DeleteObject[nx["Session"]]

Create a new multi-digraph:

In[108]:=
nx = ResourceFunction["NetworkXObject"][]
Out[108]=
In[109]:=
g = nx["MultiDiGraph"[{{2, 1}, {2, 1}, {2, 4}, {1, 3}, {1, 2}}]]
Out[109]=
In[110]:=
Graph[Normal[g], VertexLabels -> Automatic, EdgeLabels -> "EdgeTag"]
Out[110]=

Test whether a node is in the graph:

In[111]:=
MemberQ[g["Nodes"], 2]
Out[111]=
In[112]:=
Normal[%]
Out[112]=

Test if an edge is in the graph:

In[113]:=
MemberQ[g["Edges"], {2, 1}] // Normal
Out[113]=

Test if an edge with a specific tag is in the graph:

In[114]:=
MemberQ[g["Edges"], {2, 1, 1}] // Normal
Out[114]=

Use the DirectedEdge wrapper in the edge specification:

In[115]:=
Normal /@ {MemberQ[g["Edges"], 2 \[DirectedEdge] 1], MemberQ[g["Edges"], DirectedEdge[2,1,1]]}
Out[115]=
In[116]:=
DeleteObject[nx["Session"]]

Create a new multi-digraph:

In[117]:=
nx = ResourceFunction["NetworkXObject"][]
Out[117]=
In[118]:=
g = nx["MultiDiGraph"[{{2, 1}, {2, 1}, {2, 4}, {1, 3}, {1, 2}}]]
Out[118]=

Get an Association of neighbors (adjacencies) as a property of the graph:

In[119]:=
g["Adj"]
Out[119]=
In[120]:=
Normal[%]
Out[120]=

Alternatively, use the "Adjacency" method to get a list of tuples rather than an Association:

In[121]:=
g["Adjacency"[]]
Out[121]=
In[122]:=
Normal[%]
Out[122]=
In[123]:=
DeleteObject[nx["Session"]]

Create a new multi-digraph:

In[124]:=
nx = ResourceFunction["NetworkXObject"][]
Out[124]=
In[125]:=
g = nx["MultiDiGraph"[{{2, 1}, {2, 1}, {2, 4}, {1, 3}, {1, 2}}]]
Out[125]=

Get an object containing vertex degrees for all vertices in the graph:

In[126]:=
g["Degree"]
Out[126]=
In[127]:=
Normal[%]
Out[127]=

The degree of a specific vertex:

In[128]:=
g["Degree"[2]]
Out[128]=
In[129]:=
DeleteObject[nx["Session"]]

Create a new multi-digraph:

In[130]:=
nx = ResourceFunction["NetworkXObject"][]
Out[130]=
In[131]:=
g = nx["MultiDiGraph"[{{2, 1}, {2, 1}, {2, 4}, {1, 3}, {1, 2}}]]
Out[131]=

Get a list of neighbors for a node:

In[132]:=
g["Neighbors"[2]]
Out[132]=
In[133]:=
Normal[%]
Out[133]=

Or equivalently, for a directed graph:

In[134]:=
g["Successors"[2]] // Normal
Out[134]=

Predecessors of a node of a directed graph:

In[135]:=
g["Predecessors"[2]] // Normal
Out[135]=
In[136]:=
DeleteObject[nx["Session"]]

Create a new graph:

In[137]:=
nx = ResourceFunction["NetworkXObject"][]
Out[137]=
In[138]:=
g = nx["Graph"[]]
Out[138]=

Use the special attribute "weight" to create a waited graph:

In[139]:=
g["AddEdge"[1, 2, "weight" -> 4.7 ]]

Alternatively, use the AddWeightedEdgesFrom method:

In[140]:=
g["AddWeightedEdgesFrom"[{{2, 3, 7.5}, {3, 1, 5}}]]

Compute the weighted adjacency matrix on the Python side:

In[141]:=
nx["AdjacencyMatrix"[g]]
Out[141]=

Import the matrix as SparseArray:

In[142]:=
m = Normal[%]
Out[142]=
In[143]:=
MatrixForm[%]
Out[143]=

The imported graph is weighted too:

In[144]:=
gg = Normal[g]
Out[144]=
In[145]:=
WeightedGraphQ[%]
Out[145]=
In[146]:=
AnnotationValue[gg, EdgeWeight]
Out[146]=
In[147]:=
WeightedAdjacencyMatrix[gg]
Out[147]=

Compare with the adjacency matrix computed in Python:

In[148]:=
Normal[%] - m
Out[148]=
In[149]:=
DeleteObject[nx["Session"]]

Basic Graph Types (4) 

Create a new NetworkX object:

In[150]:=
nx = ResourceFunction["NetworkXObject"][]
Out[150]=
In[151]:=
edges = {1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 2};

Undirected and directed graphs with self-loops and a single edge between nodes:

In[152]:=
{nx["Graph"[edges]], nx["DiGraph"[edges]]}
Out[152]=
In[153]:=
Normal /@ %
Out[153]=
In[154]:=
LoopFreeGraphQ /@ %
Out[154]=

Undirected and directed graphs possibly with parallel edges between nodes:

In[155]:=
{nx["MultiGraph"[edges]], nx["MultiDiGraph"[edges]]}
Out[155]=
In[156]:=
Normal /@ %
Out[156]=
In[157]:=
MultigraphQ /@ %
Out[157]=

Edges in imported multigraphs are tagged:

In[158]:=
EdgeList /@ %%
Out[158]=
In[159]:=
DeleteObject[nx["Session"]]

Graph Creation (13) 

Build a graph incrementally:

In[160]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["Graph"[]]
Out[160]=
In[161]:=
g["AddEdgesFrom"[{{1, 2}, {2, 3}}]]
In[162]:=
g["AddNode"[4]]
In[163]:=
g // Normal
Out[163]=
In[164]:=
DeleteObject[nx["Session"]]

Create from an edge list:

In[165]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Graph"[{{1, 2}, {2, 3}}]] // Normal
Out[165]=

Alternatively, use the edge list in the form returned by EdgeList:

In[166]:=
EdgeList[%]
Out[166]=
In[167]:=
nx["Graph"[%]] // Normal
Out[167]=
In[168]:=
DeleteObject[nx["Session"]]

Form an Association mapping nodes to neighbors:

In[169]:=
adjacencyAssoc = <|0 -> {1, 2}, 1 -> {0, 2}, 2 -> {0, 1}|>
Out[169]=
In[170]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Graph"[adjacencyAssoc]] // Normal
Out[170]=
In[171]:=
DeleteObject[nx["Session"]]

Form a general Wolfram Language Graph:

In[172]:=
Graph[Thread[Range[5] -> RandomSample[Range[5]]]]
Out[172]=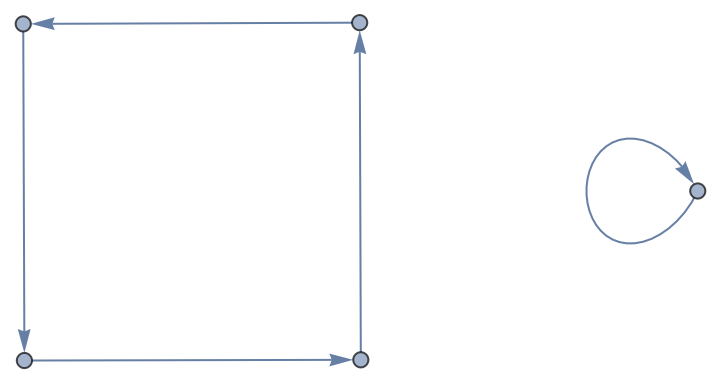
In[173]:=
nx["DiGraph"[%]] // Normal
Out[173]=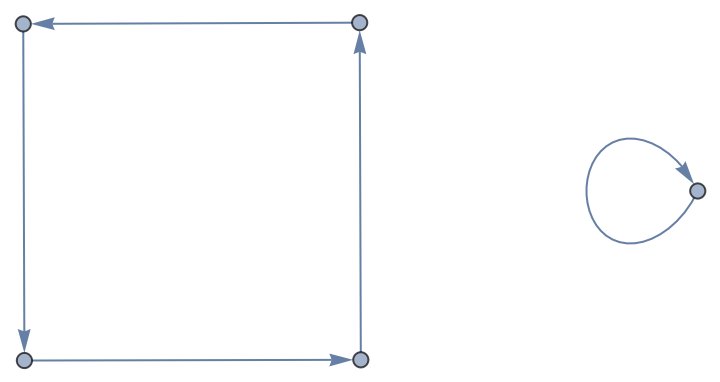

From a sparse matrix graph:

In[174]:=
m = SparseArray[{{i_, j_} /; 0 < Abs[i - j] <= 3 -> 1}, {6, 6}]
Out[174]=
In[175]:=
AdjacencyGraph[m]
Out[175]=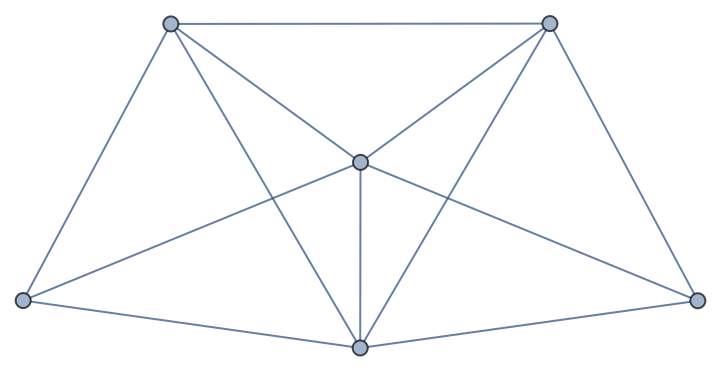
In[176]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Graph"[%]] // Normal
Out[176]=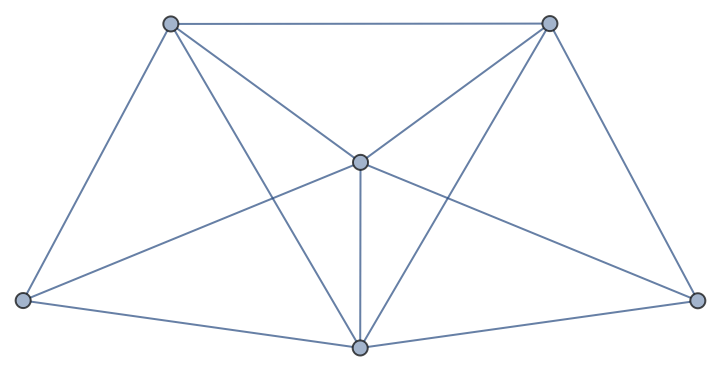
In[177]:=
DeleteObject[nx["Session"]]

From a weighted Graph object:

In[178]:=
showWeightOptions = {VertexLabels -> "VertexWeight", EdgeLabels -> "EdgeWeight"};
In[179]:=
Graph[{1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1}, VertexWeight -> Range[3], EdgeWeight -> 10 + Range[3], showWeightOptions]
Out[179]=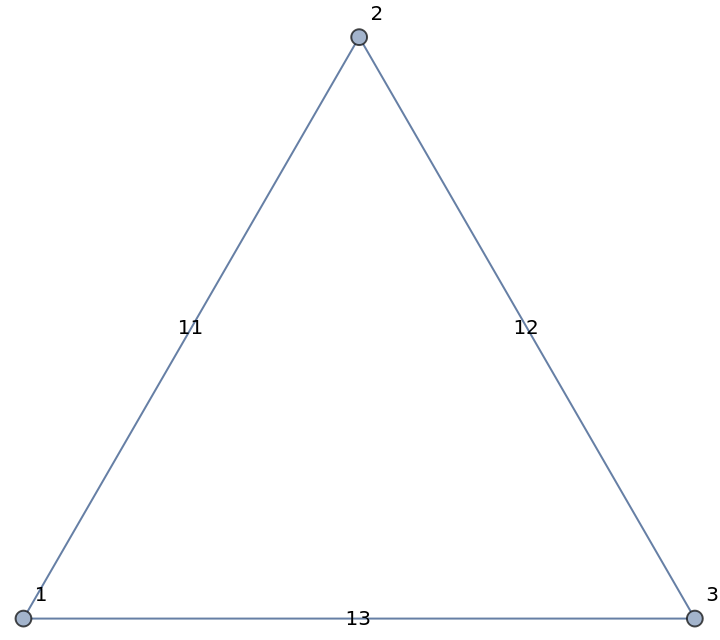
In[180]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Graph"[%]]
Out[180]=
In[181]:=
Graph[Normal[%], showWeightOptions]
Out[181]=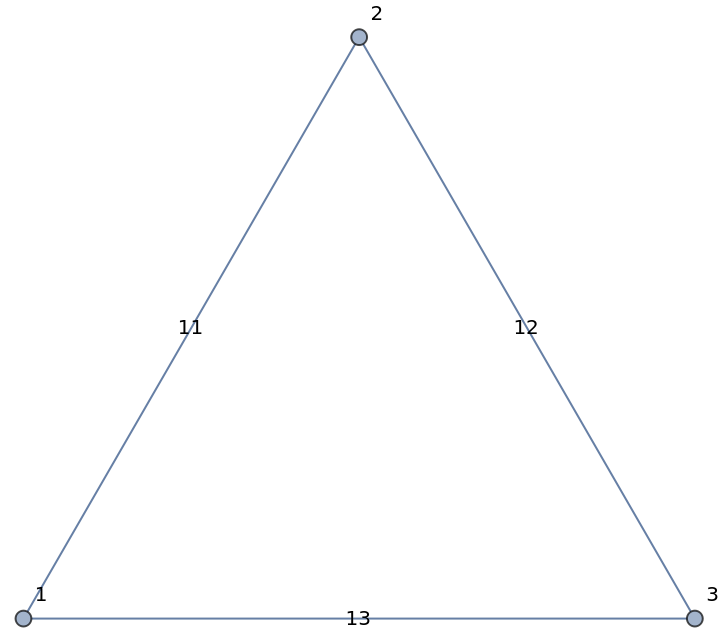
In[182]:=
DeleteObject[nx["Session"]]

From an edge-capacity and vertex-capacity Graph object:

In[183]:=
Graph[{1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1}, EdgeCapacity -> {2, 3, 4}, VertexCapacity -> {5, 6, 7}]
Out[183]=

Send the graph through NetworkX:

In[184]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Graph"[%]]
Out[184]=
In[185]:=
Graph[Normal[%]]
Out[185]=

The capacity is preserved as an annotation:

In[186]:=
AnnotationValue[{%, {1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 3}}, "capacity"]
Out[186]=
In[187]:=
AnnotationValue[{%%, {1, 2, 3}}, "capacity"]
Out[187]=
In[188]:=
DeleteObject[nx["Session"]]

From a multigraph:

In[189]:=
g = \!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2}, {{{1, 2}, {1, 2}, {2, 1}}, Null, {0, 1, Null}}]]}, TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData[" 1:eJxV0L1KA0EUBeDBZquFJYVVFDSQFIIEEdRCTyqxEPGnMdtoghbaWFhYKAhL tBLWVhJ8g0CwiSjmuKAkeYJgIQRRxERlHkHD3C3mwjAzMMw93x0rHqzvDiml xv/XYDeloazSjE+L6dLw9fwXvJafSfzc8GQyOD4sfSJ3dNfsFOr066d7+ukD uWqqX5m458ZUpjOi3rEdNIuppQadi0TXmXlDa/q83fYf2Vtx0w/7XWxe7jwv zEX08rVCZfYVNT/8/W5EDK8G9QK9djt61o9YNnfG96R5z/i9Nv8x/s81/Rj3 y5s8XJU8WyYvs5I3MB5mxbNsvFTiFT/FD/FT/BA/xQ/xU/xw7Dzo2Xnh2R6E thdlex5I2vOCtucJ1543xA/xQ/wQP8QP8UP8ED/+ADqSCu8= "], { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[ BezierCurveBox[{1, {0., -0.32888149436623243`}, 2}], 0.02261146496815286], ArrowBox[{1, 2}, 0.02261146496815286], ArrowBox[ BezierCurveBox[{2, {0., 0.32888149436623243`}, 1}], 0.02261146496815286]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02261146496815286], DiskBox[2, 0.02261146496815286]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->"NetworkGraphics", FormatType->TraditionalForm, FrameTicks->None]\);
In[190]:=
nx = ResourceFunction["NetworkXObject"][]; nx["MultiDiGraph"[g]]
Out[190]=
In[191]:=
Normal[%]
Out[191]=
In[192]:=
DeleteObject[nx["Session"]]

From another NetworkX graph:

In[193]:=
nx = ResourceFunction["NetworkXObject"][]; (dg = nx["DiGraph"[{{1, 2}, {2, 3}, {3, 1}}]]) // Normal
Out[193]=
In[194]:=
nx["Graph"[dg]] // Normal
Out[194]=
In[195]:=
DeleteObject[nx["Session"]]

Form a 2D NumPy array:

In[196]:=
arr = NumericArray@RandomInteger[{0, 1}, {10, 10}]
Out[196]=

Create a graph and import it:

In[197]:=
nx = ResourceFunction["NetworkXObject"][]; np = ResourceFunction["PythonObject"][ nx["Session"], <|"Command" -> "``", "TemplateArguments" -> {arr}|>]
Out[197]=
In[198]:=
nx["Graph"[%]] // Normal
Out[198]=

The same NumPy array can be supplied implicitly, as long as the array is in the form of NumericArray:

In[199]:=
nx["Graph"[arr]] // Normal
Out[199]=
In[200]:=
DeleteObject[nx["Session"]]

Create a graph from a SciPy sparse matrix:

In[201]:=
nx = ResourceFunction["NetworkXObject"][]; scipy = ResourceFunction["SciPyObject"][nx["Session"]]
Out[201]=
In[202]:=
s = SparseArray[{{i_, j_} /; Mod[2 i + j, 7] == 1 -> 1}, {20, 20}]
Out[202]=
In[203]:=
scipy["csr_matrix"[s]]
Out[203]=
In[204]:=
nx["Graph"[%]] // Normal
Out[204]=

Or from a SciPy sparse array:

In[205]:=
scipy["csr_array"[s]]
Out[205]=
In[206]:=
nx["Graph"[%]] // Normal
Out[206]=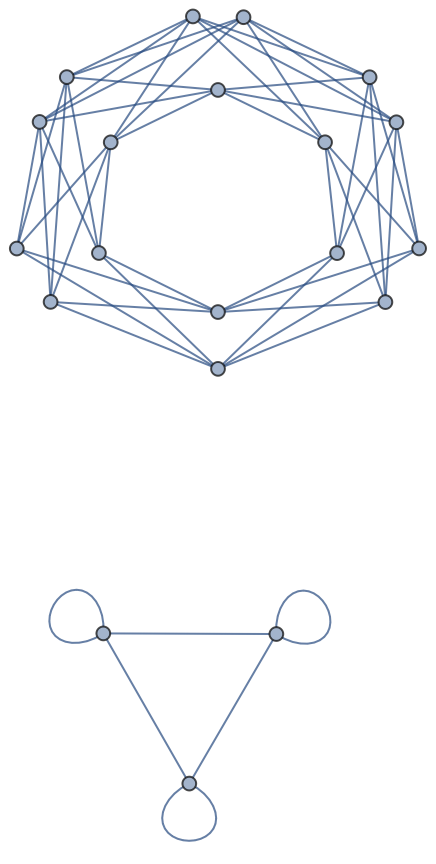
In[207]:=
DeleteObject[nx["Session"]]

Create a graph directly from a SparseArray object:

In[208]:=
s = SparseArray[{Band[{2, 1}] -> 1, Band[{3, 1}] -> 1}, {10, 10}]; nx = ResourceFunction["NetworkXObject"][]; Normal[nx["Graph"[s]]]
Out[208]=
In[209]:=
DeleteObject[nx["Session"]]

Create a data frame from a pandas object:

In[210]:=
nx = ResourceFunction["NetworkXObject"][]; pd = ResourceFunction["PandasObject"][nx["Session"]]; df = pd["DataFrame"[{{1, 1}, {2, 1}}]]
Out[208]=

Create a graph:

In[211]:=
nx["Graph"[df]]
Out[211]=

Or use the FromPandasAdjacency function:

In[212]:=
nx["FromPandasAdjacency"[df]]
Out[212]=
In[213]:=
Normal /@ {%, %%}
Out[213]=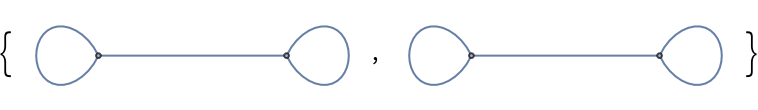
In[214]:=
DeleteObject[nx["Session"]]

Create a data frame representing a pandas edge list:

In[215]:=
nx = ResourceFunction["NetworkXObject"][]; pd = ResourceFunction["PandasObject"][nx["Session"]]; df = pd["DataFrame"[<|"source" -> {0, 1, 2, 0}, "target" -> {2, 2, 3, 2}, "my_edge_key" -> {"A", "B", "C", "D"}, "weight" -> {3, 4, 5, 6}, "color" -> {"red", "blue", "blue", "blue"}|>]]
Out[208]=

Convert to a graph:

In[216]:=
g = nx["FromPandasEdgeList"[ df, "EdgeKey" -> "my_edge_key", "EdgeAttr" -> {"weight", "color"}, "CreateUsing" -> nx["MultiGraph"[]] ] ]
Out[216]=

See the Graph:

In[217]:=
Graph[Normal[%], VertexLabels -> Automatic]
Out[217]=

See the edge list and weights:

In[218]:=
Grid[{EdgeList[%], EdgeWeight /. Options[%], "color" /. (EdgeList[%] /. (AnnotationRules /. Options[%]))}, Dividers -> All]
Out[218]=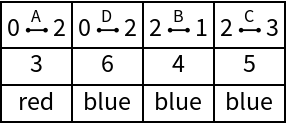

Compare with a dataset:

In[219]:=
Normal[df]
Out[219]=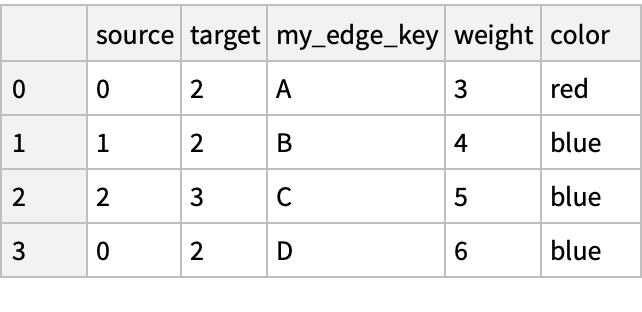
In[220]:=
DeleteObject[nx["Session"]]

Graph Generators (8) 

Explore the variety of ways to generate graphs:

In[221]:=
session = StartExternalSession["Python"];
In[222]:=
ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "Generators"]]
Out[222]=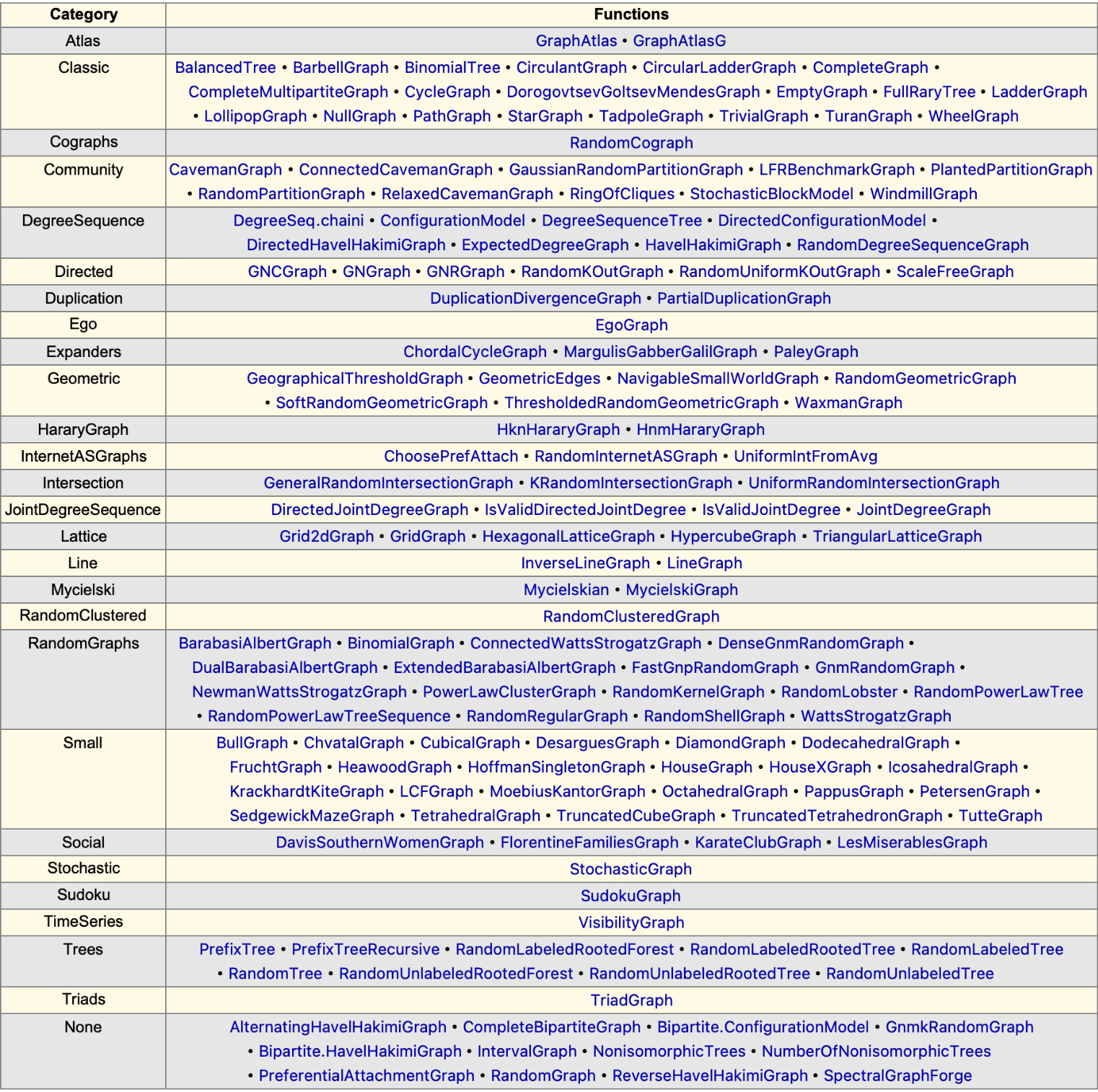
In[223]:=
DeleteObject[session]

Create the first few scale-free pseudo-fractal graphs using the Dorogovtsev-Goltsev-Mendes algorithm:

In[224]:=
nx = ResourceFunction["NetworkXObject"][]; (Normal@nx["DorogovtsevGoltsevMendesGraph"[#]]) & /@ Range[0, 5]
Out[224]=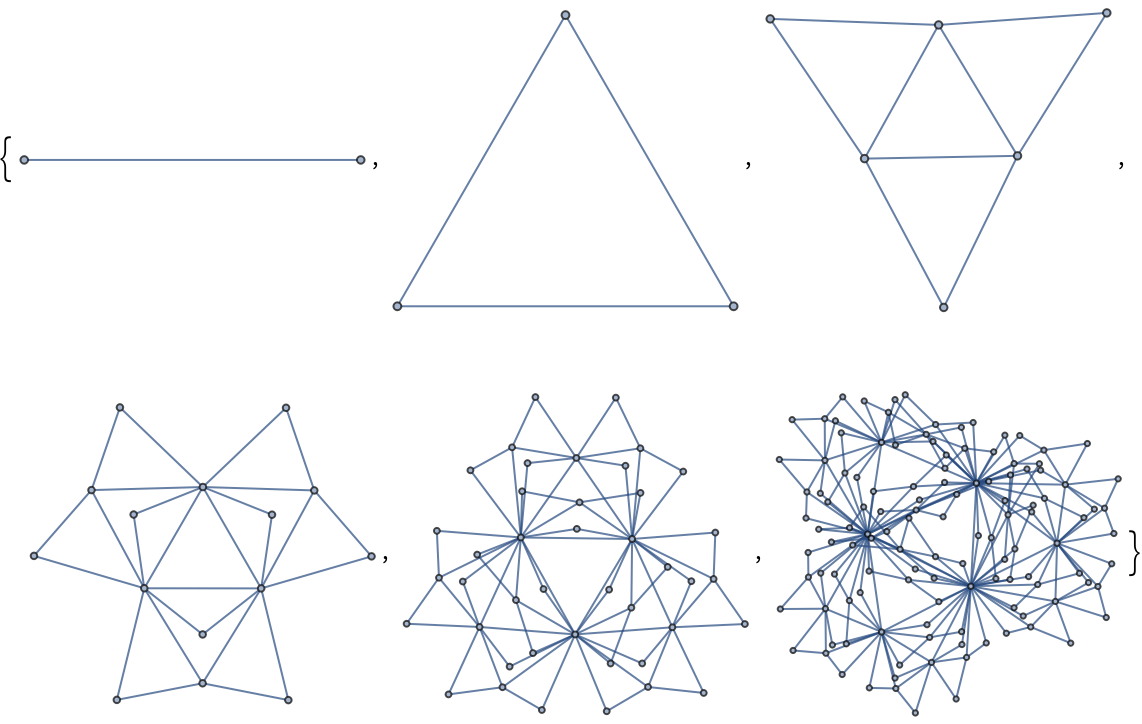
In[225]:=
DeleteObject[nx["Session"]]

A few Newman–Watts–Strogatz small-world graphs:

In[226]:=
nx = ResourceFunction["NetworkXObject"][]; Table[nx["NewmanWattsStrogatzGraph"[7, 2, .5, "Seed" -> i]] // Normal, {i, 6}]
Out[226]=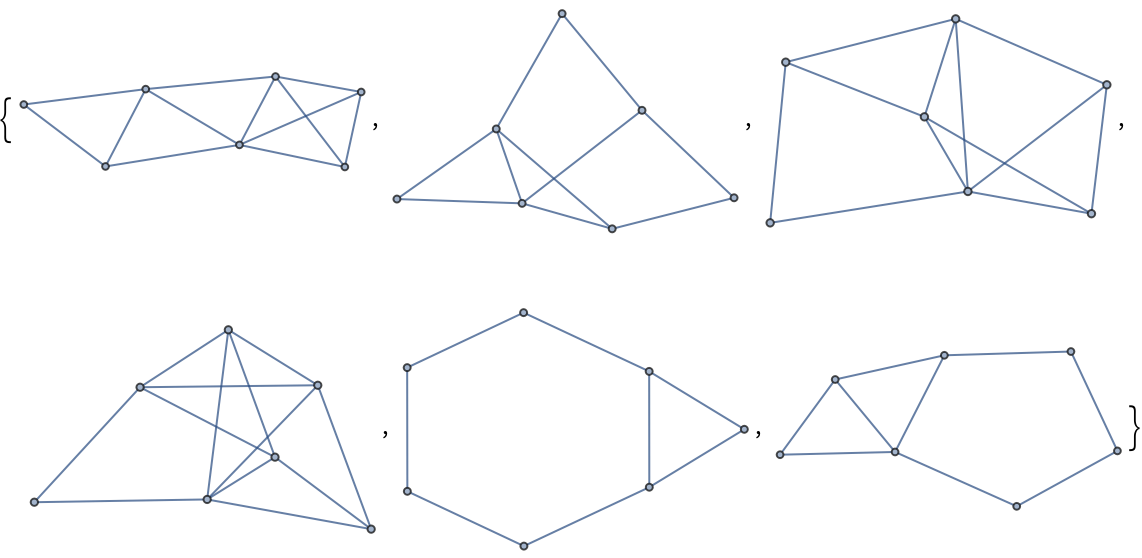
In[227]:=
DeleteObject[nx["Session"]]

The specified graph from the Graph Atlas:

In[228]:=
nx = ResourceFunction["NetworkXObject"][]; nx["GraphAtlas"[1000]] // Normal
Out[228]=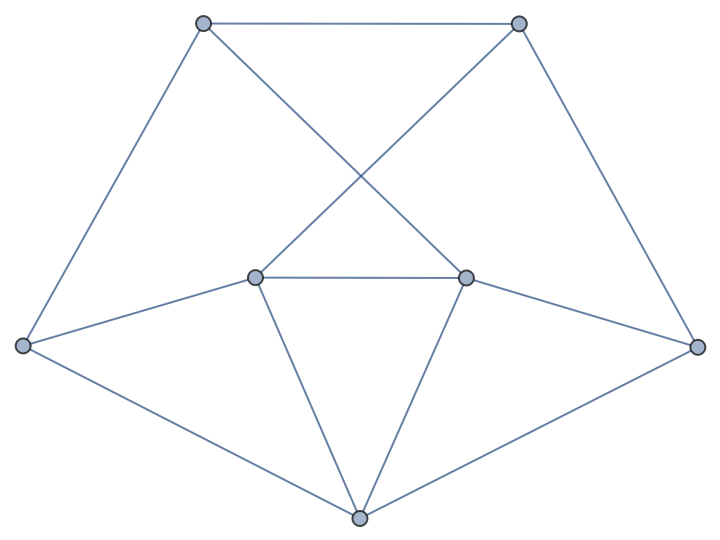
In[229]:=
DeleteObject[nx["Session"]]

A Zachary’s Karate Club graph:

In[230]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["KarateClubGraph"[]]) // Normal
Out[230]=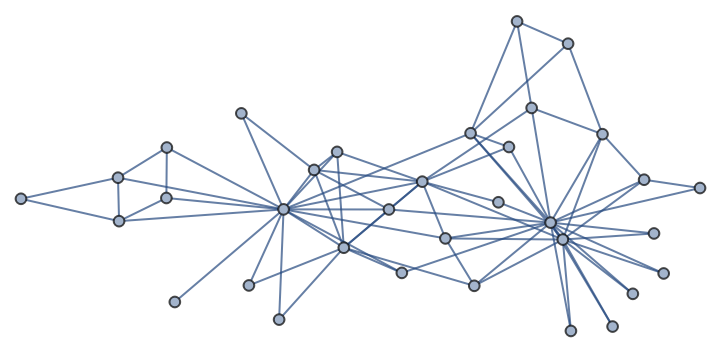

The same graph in the Wolfram Language (but note that NetworkX version is kept on the Python side):

In[231]:=
ExampleData[{"NetworkGraph", "ZacharyKarateClub"}]
Out[231]=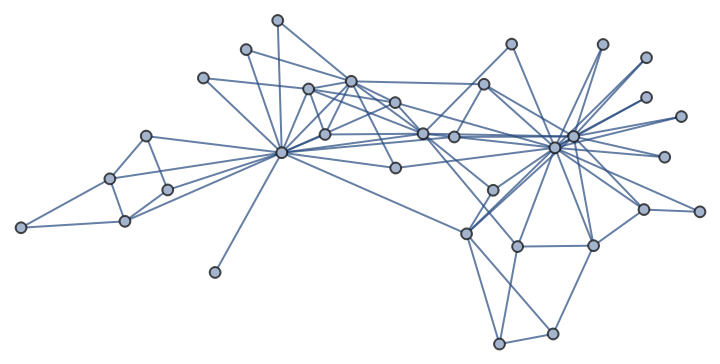

Create a series of random Spectral Graph Forge (SGF) graphs resembling the global properties of the previous graph:

In[232]:=
Table[nx["SpectralGraphForge"[g, i]] // Normal, {i, .9, .4, -.1}]
Out[232]=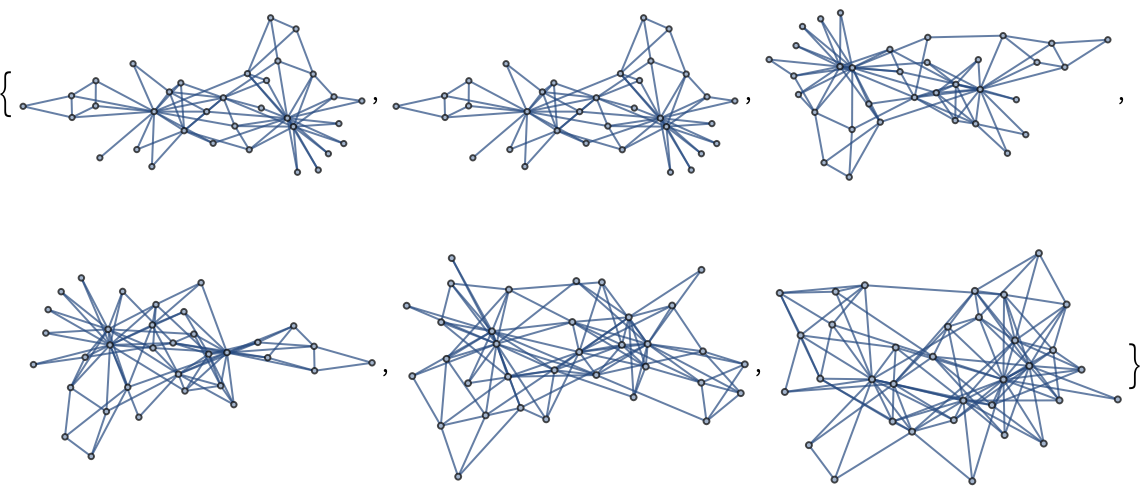
In[233]:=
DeleteObject[nx["Session"]]

A bipartite random graph with the first n nodes in the first bipartite set and the remaining m nodes in the second:

In[234]:=
n = 5; m = 10; nx = ResourceFunction["NetworkXObject"][]; nx["RandomGraph"[n, m, .75, "Seed" -> 1]] // Normal
Out[234]=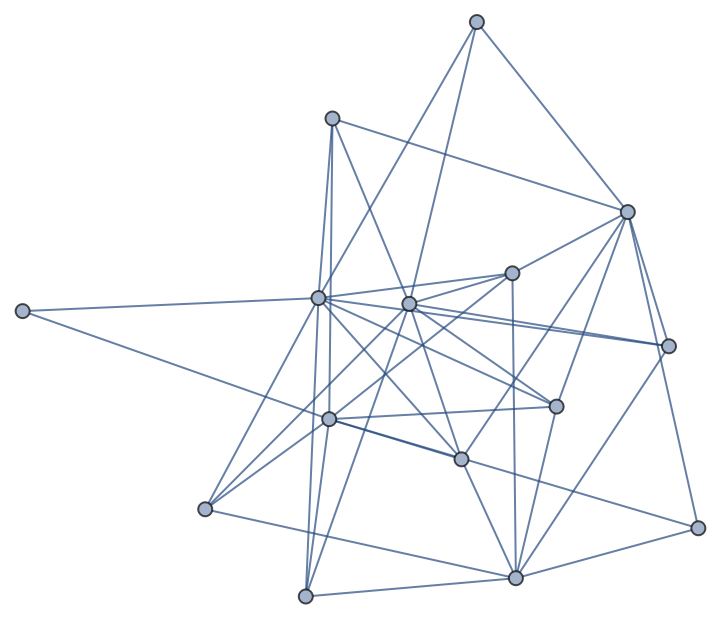

Show the bipartite partition of the graph:

In[235]:=
Graph[%, GraphLayout -> "BipartiteEmbedding", VertexLabels -> Automatic]
Out[235]=
In[236]:=
DeleteObject[nx["Session"]]

A random partition graph:

In[237]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["RandomPartitionGraph"[{10, 10, 10}, 0.25, 0.01, "Seed" -> 1]] // Normal
Out[237]=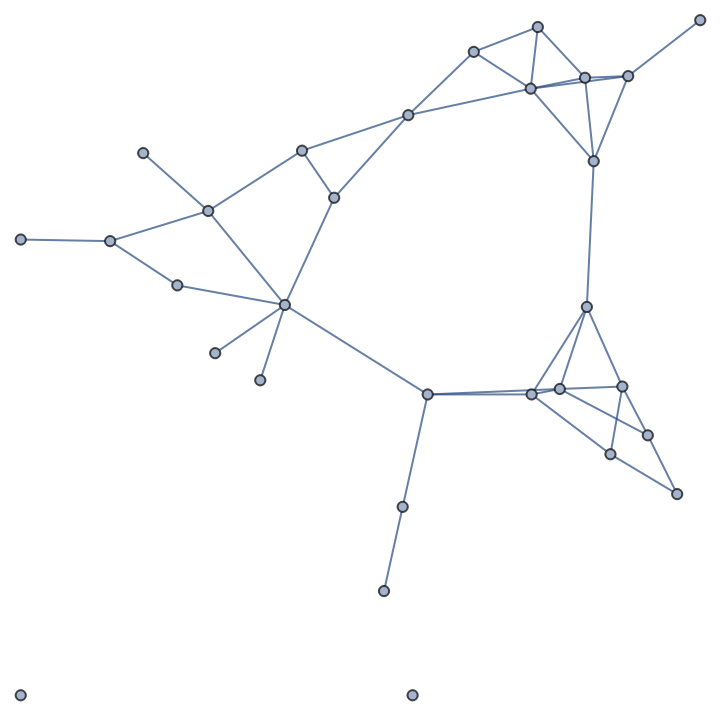
In[238]:=
AnnotationValue[g, "partition"]
Out[238]=
In[239]:=
DeleteObject[nx["Session"]]

A Gaussian random partition graph:

In[240]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["GaussianRandomPartitionGraph"[100, 20, 10, 0.5, 0.01, "Seed" -> 123]] // Normal
Out[240]=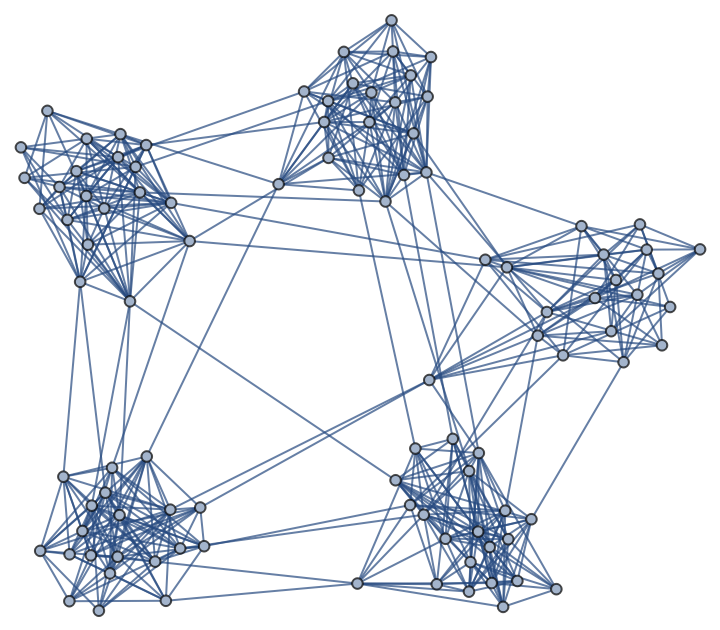
In[241]:=
AnnotationValue[g, "partition"]
Out[241]=

Highlight the partitions:

In[242]:=
HighlightGraph[g, %]
Out[242]=

Graph Functions (2) 

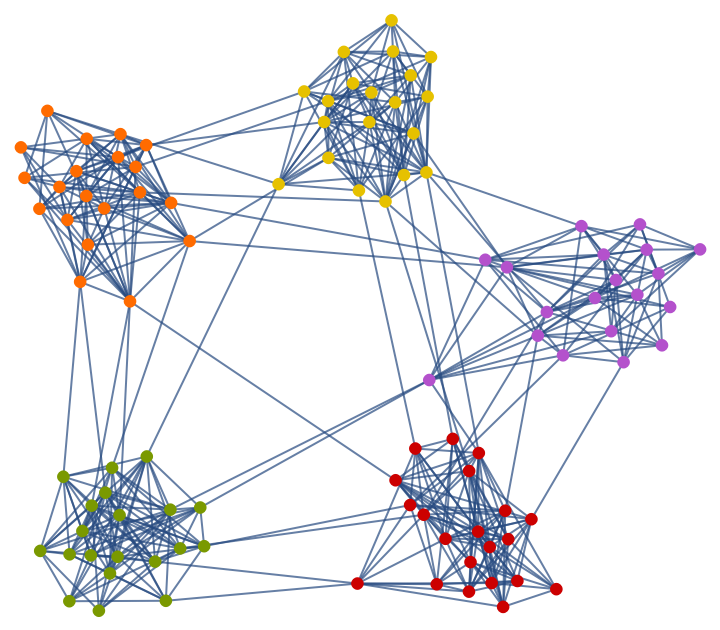Explore functional interface to graph methods and assorted graph utilities:

In[243]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "Classes"]]
Out[243]=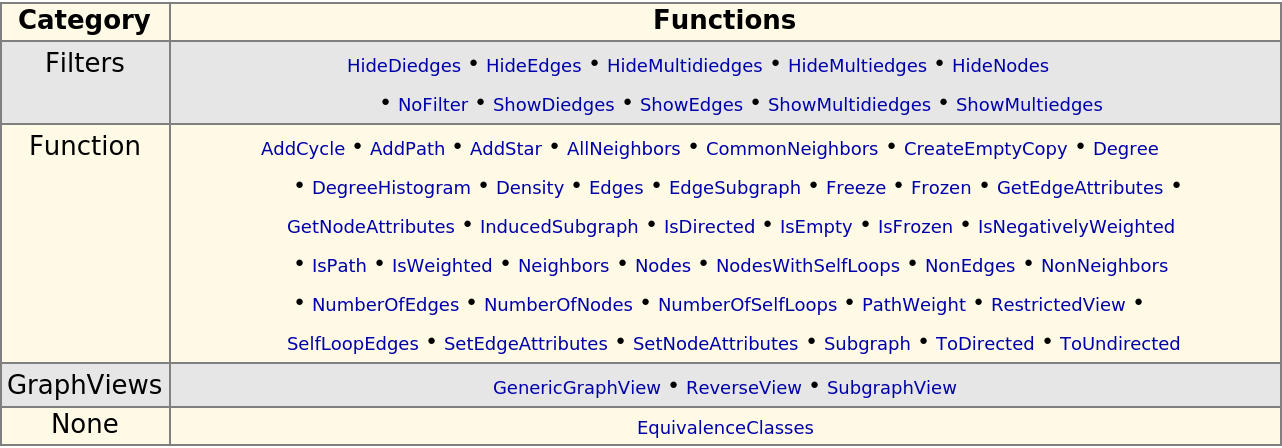
In[244]:=
DeleteObject[session]

Add a star to a graph, with the first node in the middle of the star and the other nodes connected to it:

In[245]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["Graph"[]]; nx["AddStar"[g, {0, 1, 2, 3}]]
In[246]:=
Graph[g // Normal, VertexLabels -> Automatic]
Out[246]=

Add another star, with weighted edges:

In[247]:=
nx["AddStar"[g, {2, 10, 11, 12, 13, 14}, "Weight" -> 2]]
In[248]:=
Graph[g // Normal, VertexLabels -> Automatic, EdgeLabels -> "EdgeWeight"]
Out[248]=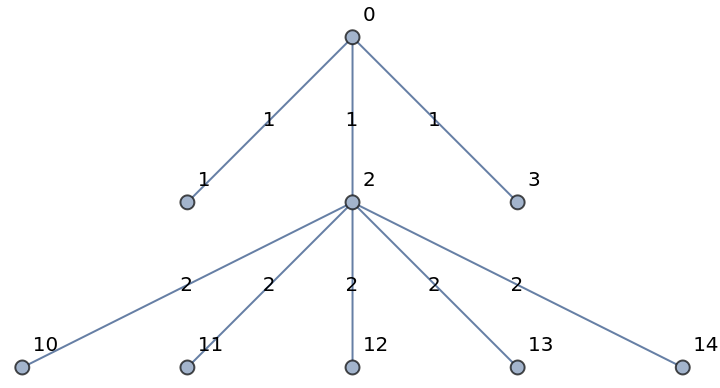
In[249]:=
DeleteObject[nx["Session"]]

Algorithms (7) 

Explore available graph-theoretic algorithms:

In[250]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "Algorithms"]]
Out[250]=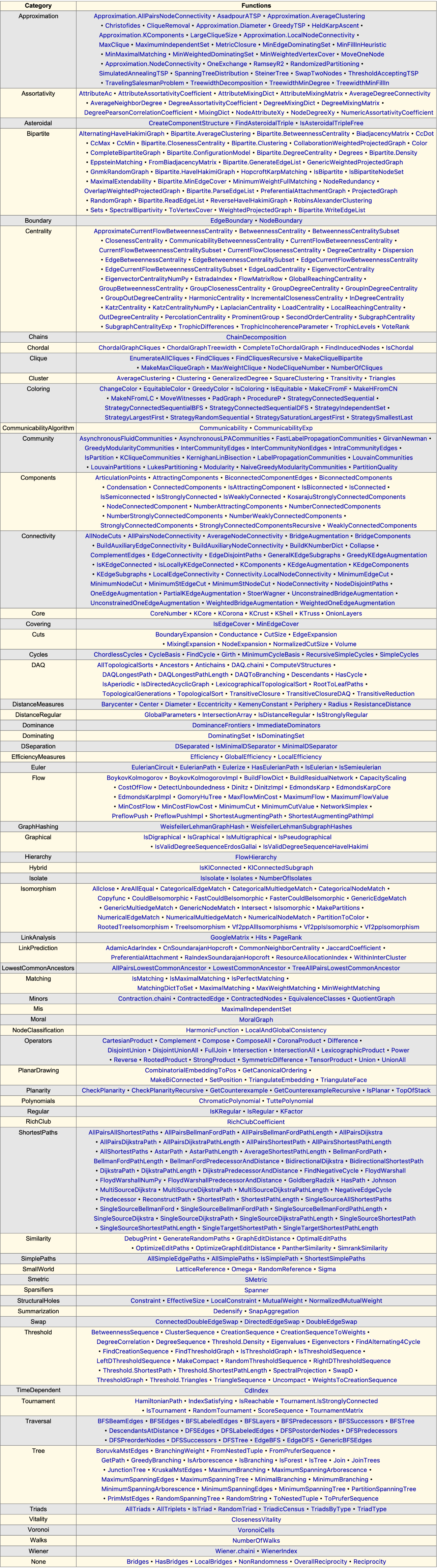
In[251]:=
DeleteObject[session]

Create a random bipartite graph with n nodes in the first bipartite set and compute the biadjacency matrix of the graph:

In[252]:=
nx = ResourceFunction["NetworkXObject"][]; n = 5; g = nx["RandomGraph"[n, 10, .75, "Seed" -> 1]]
Out[252]=
In[253]:=
nx["BiadjacencyMatrix"[g, Range[0, n - 1]]]
Out[253]=
In[254]:=
(bm = Normal[%]) // MatrixForm
Out[254]=

Despite being smaller, the biadjacency matrix fully describes the graph:

In[255]:=
(m = AdjacencyMatrix[Normal[g]]) // MatrixForm
Out[255]=
In[256]:=
m == ArrayFlatten[{{0, bm}, {Transpose[bm], 0}}]
Out[256]=
In[257]:=
DeleteObject[nx["Session"]]

Compute the clustering coefficient for nodes of a complete graph:

In[258]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["CompleteGraph"[5]]) // Normal
Out[258]=
In[259]:=
nx["Clustering"[g]]
Out[259]=

The clustering coefficient for the specified nodes:

In[260]:=
nx["Clustering"[g, "Nodes" -> {0, 1}]]
Out[260]=

For a single node:

In[261]:=
nx["Clustering"[g, "Nodes" -> 0]]
Out[261]=
In[262]:=
DeleteObject[nx["Session"]]

Compute the average clustering coefficient for nodes of a random Erdős-Rényi (binomial) graph:

In[263]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["ErdosRenyiGraph"[10, 0.2, "Seed" -> 10]]) // Normal
Out[263]=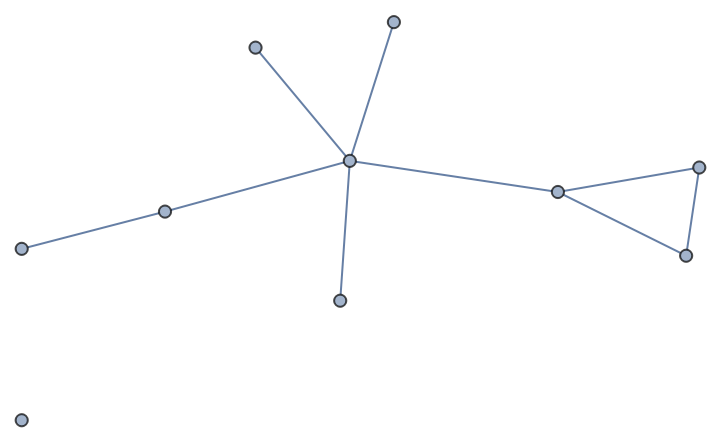
In[264]:=
nx["Approximation.AverageClustering"[g, "Trials" -> 1000, "Seed" -> 10]]
Out[264]=
In[265]:=
DeleteObject[nx["Session"]]

Find the dominating set of a random geometric graph:

In[266]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["RandomGeometricGraph"[15, .5, "Seed" -> 1]]) // Normal
Out[266]=
In[267]:=
d = nx["DominatingSet"[g]]
Out[267]=

Confirm that the set of vertices form a dominating set:

In[268]:=
HighlightGraph[Graph[Normal[g], VertexSize -> Small], d, VertexLabels -> Automatic, VertexSize -> Large]
Out[268]=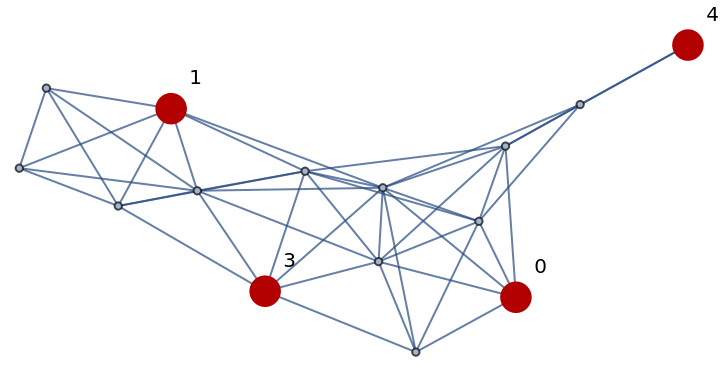
In[269]:=
nx["IsDominatingSet"[g, d]]
Out[269]=
In[270]:=
DeleteObject[nx["Session"]]

Define a hidden Markov model (HMM) graph with five states and observation nodes:

In[271]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["DiGraph"[]]
Out[271]=
In[272]:=
g["AddEdgesFrom"[{{"S1", "S2"}, {"S2", "S3"}, {"S3", "S4"}, {"S4", "S5"}, {"S1", "O1"}, {"S2", "O2"}, {"S3", "O3"}, {"S4", "O4"}, {"S5", "O5"}}]]

Check if states/observation nodes before "S3" are d-separated from the states/observations after "S3":

In[273]:=
x = {"S2", "S1", "O1", "O2"};
In[274]:=
y = {"O4", "O5", "S5", "S4"};
In[275]:=
z = {"S3"};
In[276]:=
nx["DSeparated"[g, x, y, z]]
Out[276]=
In[277]:=
HighlightGraph[ Graph[Normal[g], VertexLabels -> Automatic, VertexSize -> .1], Flatten[{Style[#, Red] & /@ x, Style[#, Green] & /@ y, Style[#, Yellow] & /@ z}]]
Out[277]=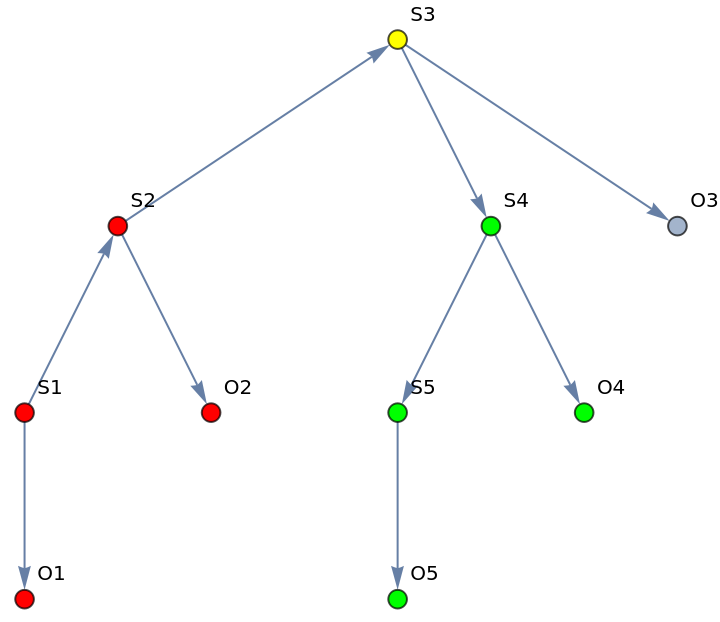
In[278]:=
DeleteObject[nx["Session"]]

Create an undirected moralized graph of given a directed graph:

In[279]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["DiGraph"[{{1, 2}, {2, 3}, {2, 5}, {3, 4}, {4, 3}}]]
Out[279]=
In[280]:=
m = nx["MoralGraph"[g]]
Out[280]=

Display the graphs:

In[281]:=
Graph[Normal[#], VertexLabels -> Automatic] & /@ {g, m}
Out[281]=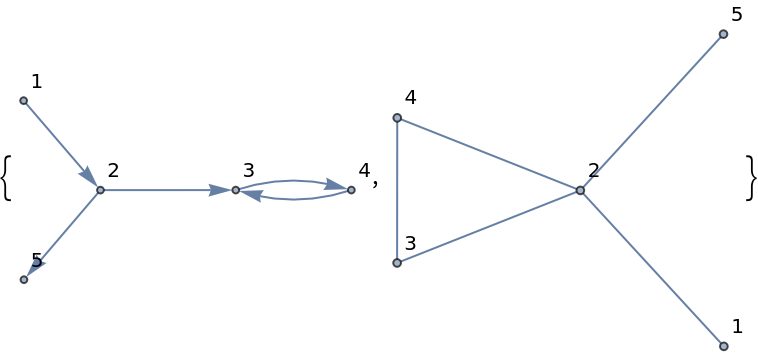

The added edge between unconnected parents that have a common child:

In[282]:=
Complement @@ Reverse[Map[Sort, List @@@ Keys[Normal[#["Edges"[]]]] & /@ {g, m}, {2}]]
Out[282]=
In[283]:=
DeleteObject[nx["Session"]]

Drawing (2) 

Functions for drawing graphs include interfaces to Python packages PyGraphviz, PyDot, PyLab:

In[284]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "Drawing"]]
Out[284]=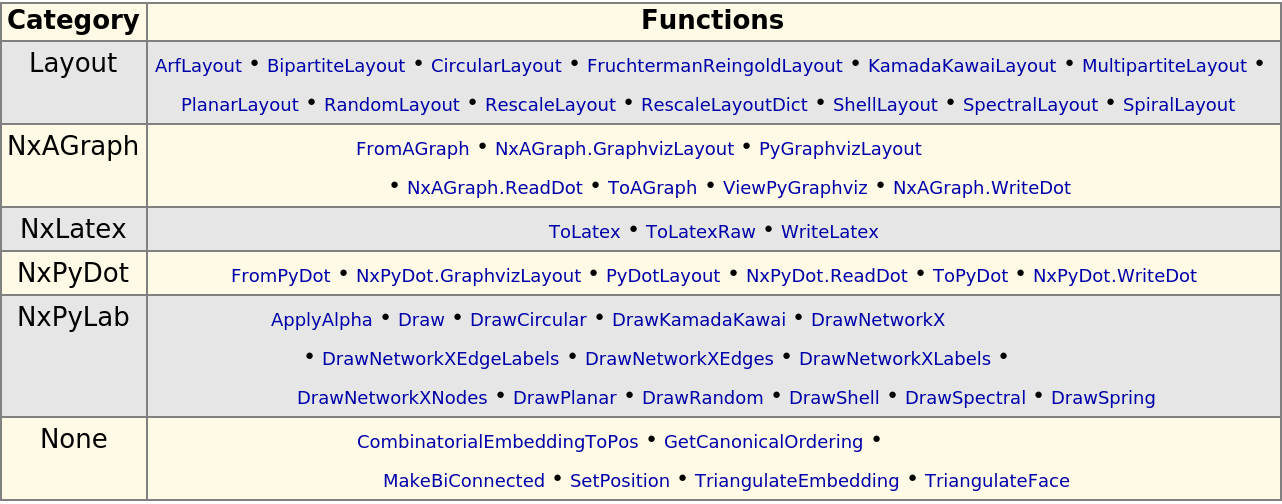
In[285]:=
DeleteObject[session]

Create a Matplotlib object to draw a graph on the Python side:

In[286]:=
session = StartExternalSession["Python"]; plt = ResourceFunction["MatplotlibObject"][session]
Out[286]=

Prepare a subplot object to plot a graph:

In[287]:=
plt["subplot"[121]]
Out[287]=

Create and plot the graph in Python:

In[288]:=
nx = ResourceFunction["NetworkXObject"][session]
Out[288]=
In[289]:=
g = nx["PetersenGraph"[]]
Out[289]=
In[290]:=
nx["Draw"[g, "WithLabels" -> True, "FontWeight" -> "bold"]]

Import the graph image:

In[291]:=
ResourceFunction["MatplotlibObject"][session, "Show"[]]
Out[291]=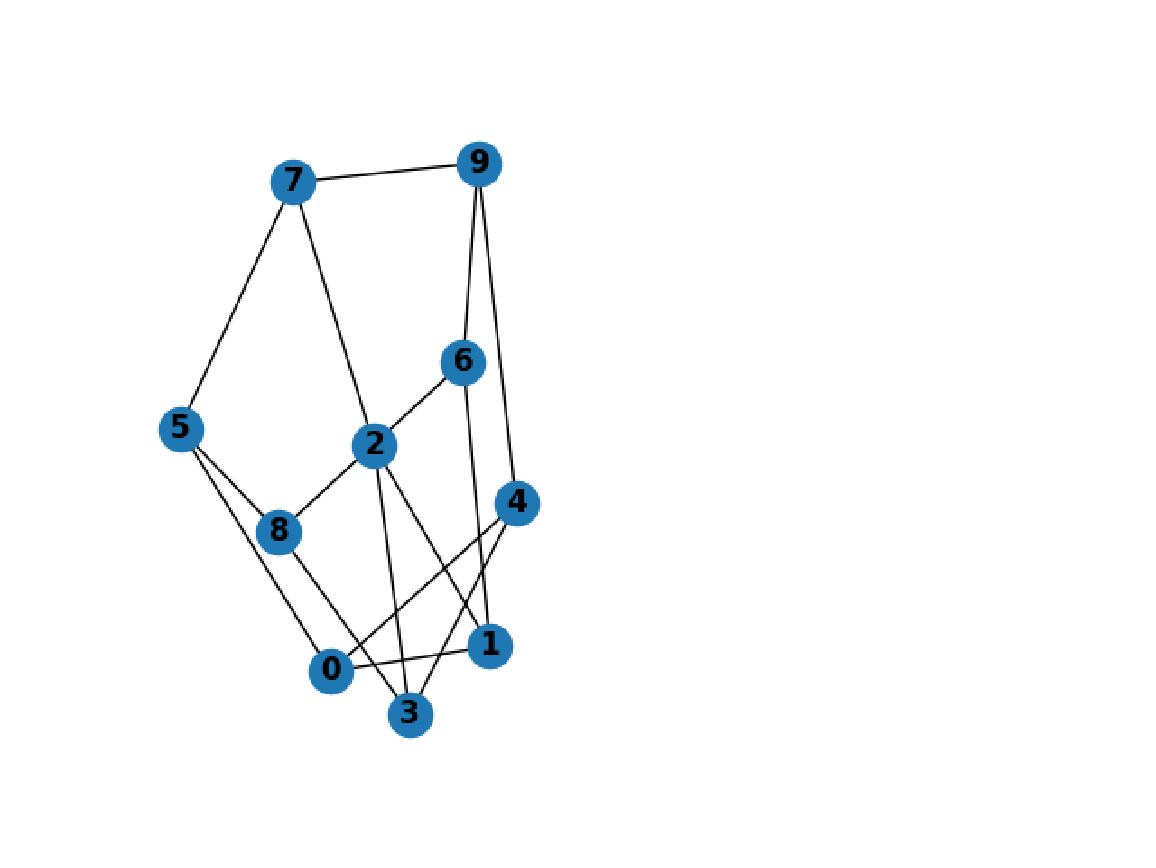

Prepare another subplot and draw the graph with shell layout:

In[292]:=
plt["subplot"[122]]
Out[292]=
In[293]:=
nx["DrawShell"[g, "nlist" -> {Range[5, 9], Range[0, 4]}, "WithLabels" -> True, "FontWeight" -> "bold"]]

Import the combined image:

In[294]:=
ResourceFunction["MatplotlibObject"][session, "Show"[]]
Out[294]=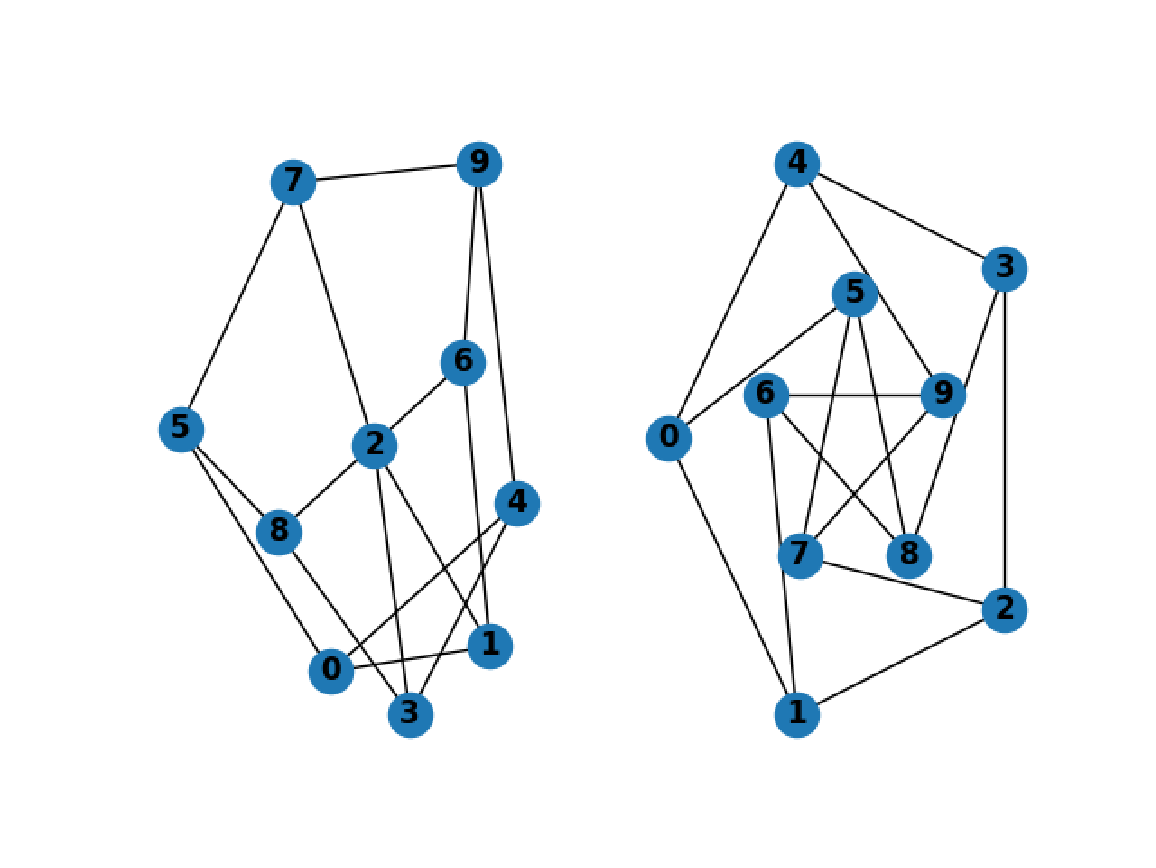
In[295]:=
DeleteObject[session]

Linear Algebra Operations (2) 

Display a table graph-theoretical functions for linear algebra:

In[296]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "LinearAlgebra"]]
Out[296]=
In[297]:=
DeleteObject[session]

Construct a simple graph with given degree sequence using the Havel-Hakimi algorithm:

In[298]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["HavelHakimiGraph"[{3, 2, 2, 1, 0}]]) // Normal
Out[298]=

The Bethe Hessian matrix of the graph:

In[299]:=
nx["BetheHessianMatrix"[g]]
Out[299]=
In[300]:=
Normal[%] // MatrixForm
Out[300]=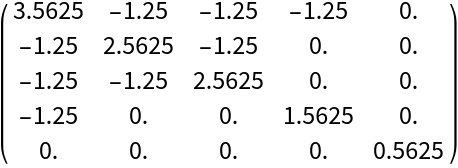
In[301]:=
DeleteObject[nx["Session"]]

Import and Export (2) 

Display a table of functions that import, export and process data in common graph formats:

In[302]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "ReadWrite"]]
Out[302]=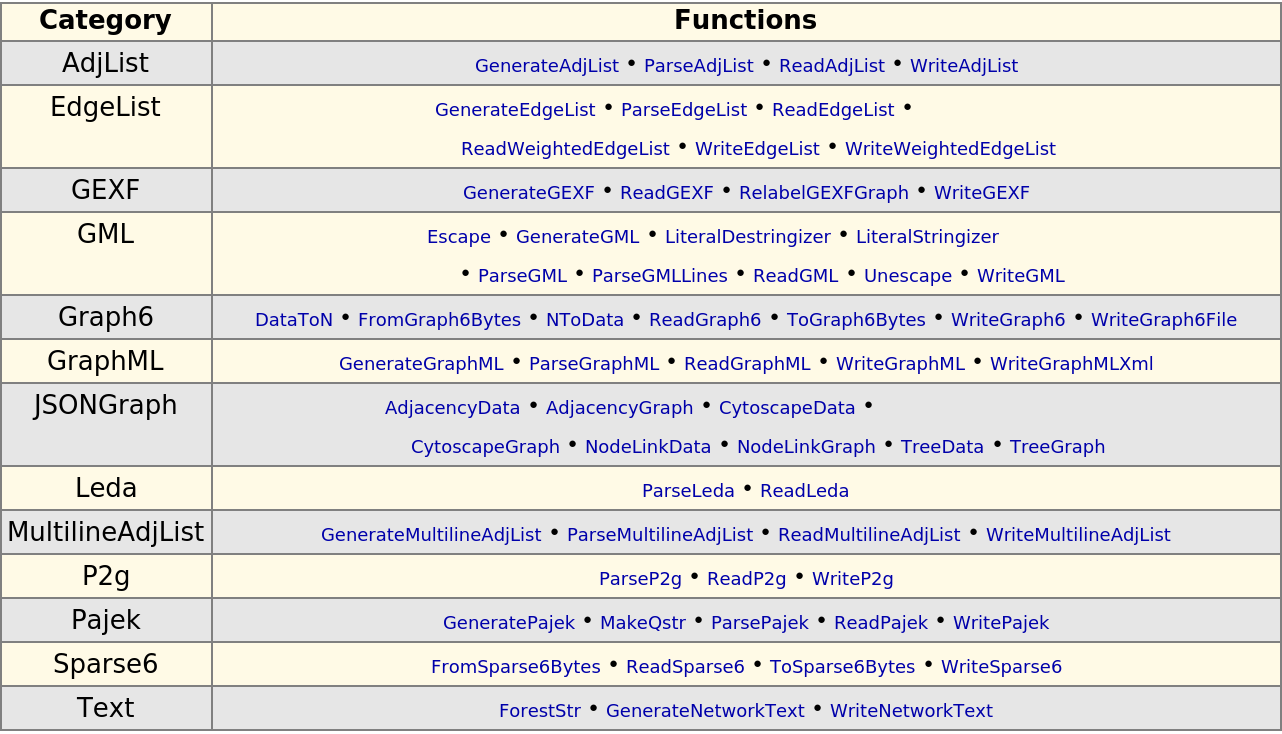
In[303]:=
DeleteObject[session]

Create a graph:

In[304]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["RandomLobster"[10, 0.5, 0.7]]) // Normal
Out[341]=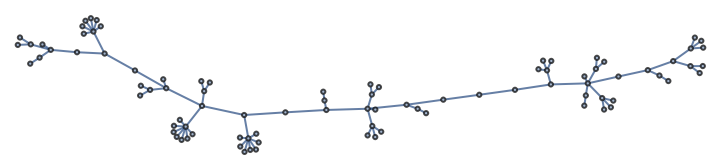

Export the graph in the Graph6 format:

In[342]:=
fname = FileNameJoin[{$TemporaryDirectory, "foo.g6"}];
In[343]:=
nx["WriteGraph6"[g, fname]]

Import the file in Python:

In[344]:=
nx["ReadGraph6"[fname]]
Out[344]=
In[345]:=
% // Normal
Out[345]=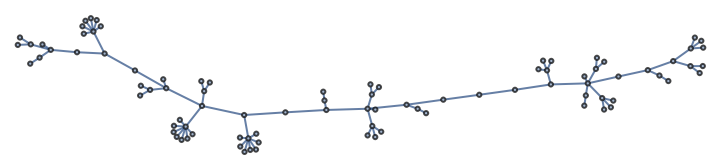

Import the file in the Wolfram Language:

In[346]:=
Import[fname]
Out[346]=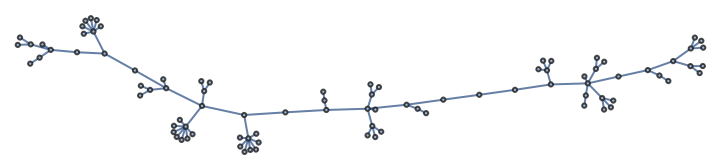
In[347]:=
DeleteObject[nx["Session"]]

Utilities and Helpers (3) 

Explore the available graph utilities:

In[348]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "utils"]]
Out[348]=

Utilities called by graph constructors that can also be called directly (and functions for converting back):

In[349]:=
ResourceFunction["NetworkXObject"][session, "Explore"["Functions", "ConvertMatrix"]]
Out[349]=
In[350]:=
DeleteObject[session]

Create an edge list using "Pairwise":

In[351]:=
nx = ResourceFunction["NetworkXObject"][]; pairwise = nx["Pairwise"[{1, 2, 3}, "cyclic" -> True]]
Out[64]=

Partition creates an analogous list:

In[352]:=
partition = Partition[{1, 2, 3}, 2, 1, 1]
Out[352]=

Create graphs from each to show the equivalence:

In[353]:=
Normal[nx["Graph"[#]]] & /@ {pairwise, partition}
Out[353]=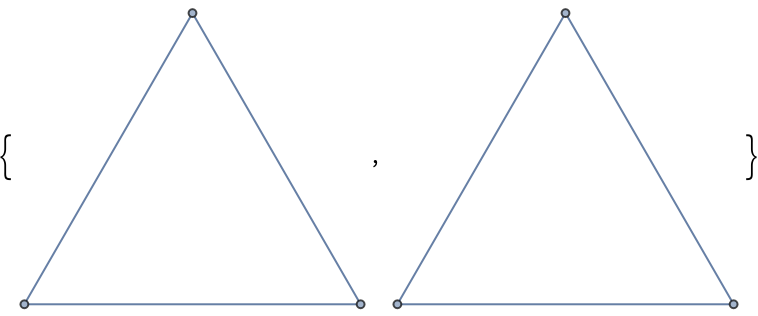
In[354]:=
DeleteObject[nx["Session"]]

Convert a graph to a SciPy sparse array:

In[355]:=
nx = ResourceFunction["NetworkXObject"][]; g = nx["Graph"[{{1, 1}, {2, 2}}]]
Out[355]=
In[356]:=
nx["ToSciPySparseArray"[g]]
Out[356]=

Import the matrix:

In[357]:=
Normal[%] // MatrixForm
Out[357]=
In[358]:=
DeleteObject[nx["Session"]]

Options (11) 

CreateUsing (1) 

Control the type of returned object in graph constructors using the option CreateUsing:

In[359]:=
nx = ResourceFunction["NetworkXObject"][]; Table[nx[ "CompleteGraph"[5, "CreateUsing" -> nx[type]]], {type, {"Graph", "DiGraph"}}]
Out[359]=
In[360]:=
Normal /@ %
Out[360]=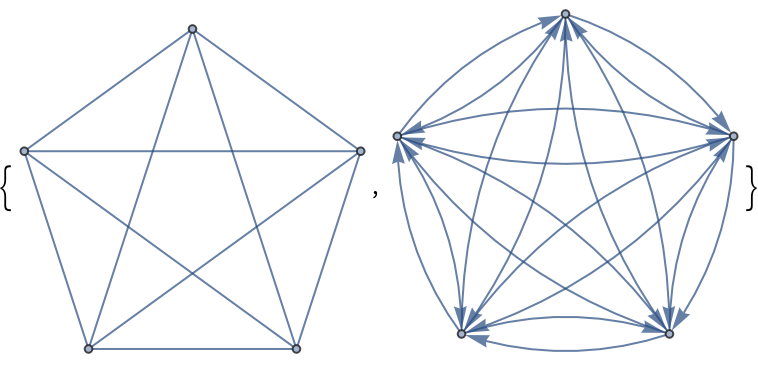
In[361]:=
DeleteObject[nx["Session"]]

Copy (6) 

Functions, such as "RelabelNodes", that have the option "Copy" allow you to modify the input graph object in-place:

In[362]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Information", "RelabelNodes"]
Out[362]=

By default, "RelabelNodes" returns a modified graph keeping the original intact:

In[363]:=
g = nx["BarbellGraph"[4, 1]]
Out[363]=

Define the remapping:

In[364]:=
mapping = AssociationThread[Range[0, 4] -> CharacterRange["a", "e"]]
Out[364]=
In[365]:=
h = nx["RelabelNodes"[g, mapping]]
Out[365]=

Show the original and remapped vertex names:

In[366]:=
Graph[Normal[#], VertexLabels -> Automatic] & /@ {g, h}
Out[366]=

Use "Copy"→False to modify the input graph in-place:

In[367]:=
nx["RelabelNodes"[g, mapping, "Copy" -> False]]
Out[367]=

The graph g has changed:

In[368]:=
Graph[Normal[g], VertexLabels -> Automatic]
Out[368]=
In[369]:=
DeleteObject[nx["Session"]]

Seed (4) 

The option "Seed" seeds the random number generator in functions that use randomness to generate, draw and compute properties or manipulate graphs.

Create a line graph:

In[370]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["PathGraph"[5]]) // Normal
Out[370]=

Define a function that computes random coordinates of a graph, passing options to RandomLayout:

In[371]:=
vCoord[g_, opts___] := Normal /@ Normal /@ nx["RandomLayout"[g, opts]]

Without a seed, executing the function twice produces different sets of random coordinates:

In[372]:=
Table[Graph[Normal[g], VertexCoordinates -> vCoord[g]], {2}]
Out[372]=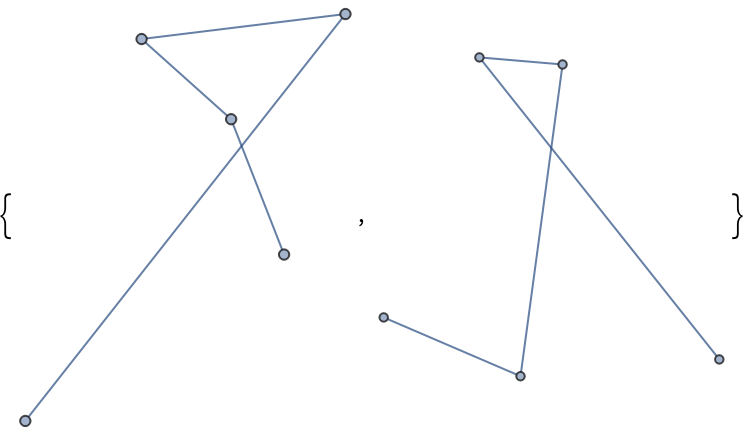

Use the option "Seed" to create a reproducible random layout:

In[373]:=
Table[Graph[Normal[g], VertexCoordinates -> vCoord[g, "Seed" -> 1]], {2}]
Out[373]=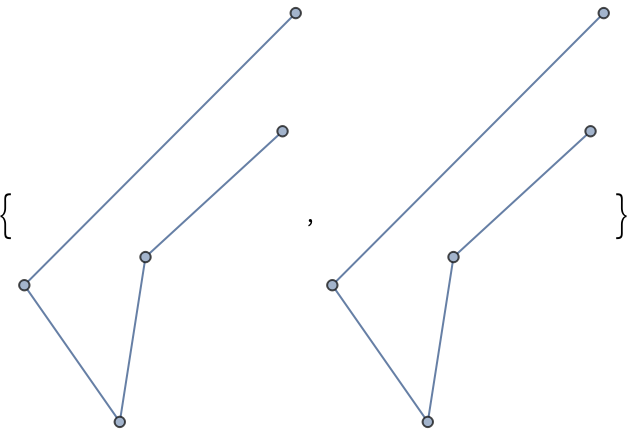
In[374]:=
DeleteObject[nx["Session"]]

Applications (3) 

Employ algorithms that might not yet be implemented in the Wolfram Language; for instance, find an approximate solution to the asymmetric traveling salesman problem using the algorithm developed by Asadpour et al.

Create a weighted directed graph:

In[375]:=
nx = ResourceFunction["NetworkXObject"][]; CompleteGraph[3, DirectedEdges -> True, EdgeWeight -> {1 \[DirectedEdge] 2 -> 2, 2 \[DirectedEdge] 3 -> 2, 3 \[DirectedEdge] 1 -> 2, 1 \[DirectedEdge] 3 -> 1, 3 \[DirectedEdge] 2 -> 1, 2 \[DirectedEdge] 1 -> 1}, VertexLabels -> Automatic, EdgeLabels -> "EdgeWeight"]
Out[375]=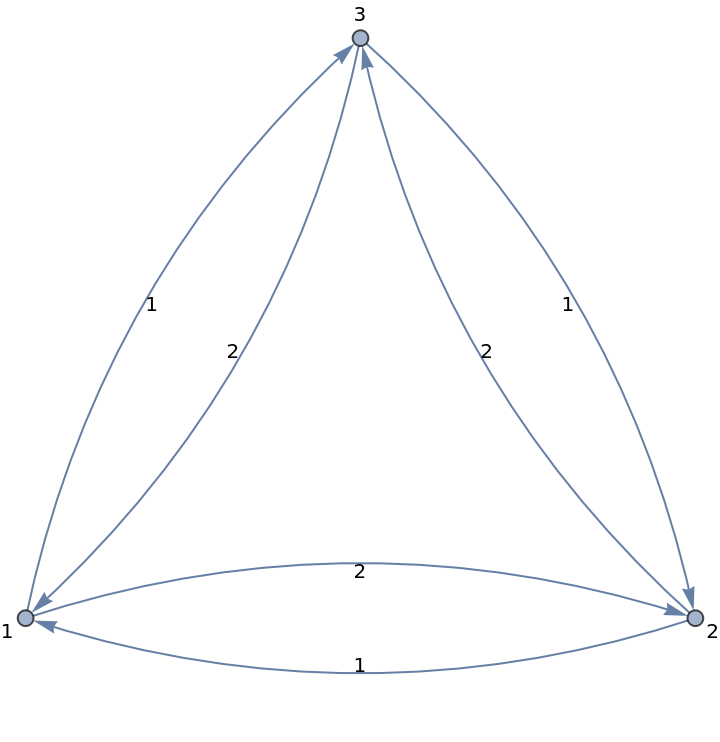

Import the graph in Python:

In[376]:=
g = nx["DiGraph"[%]]
Out[376]=

Find the shortest cycle starting and ending at vertex 1:

In[377]:=
nx["AsadpourATSP"[g, "Source" -> 1]]
Out[377]=
In[378]:=
DeleteObject[nx["Session"]]

Create a graph using a constructor that might not yet be implemented in the Wolfram Language, such as a directed graph constructor for the growing network with redirection (the GNR model):

In[379]:=
nx = ResourceFunction["NetworkXObject"][]; nx["GNRGraph"[109, .5, "Seed" -> 10]] // Normal
Out[379]=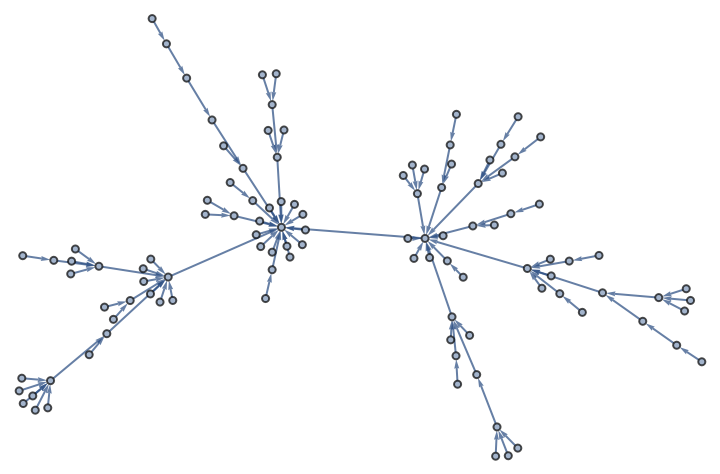
In[380]:=
DeleteObject[nx["Session"]]

Visualize data and draw conclusions from a pandas DataFrame object.

Create a small group of participants:

In[381]:=
n = 20; SeedRandom[10]; names = ResourceFunction["RandomPetName"][n]
Out[380]=

Simulate a table exported from a JIRA bug database:

In[382]:=
bugs = 100;
In[383]:=
(db = AssociationThread[{"Assignee", "Reporter"} -> RandomChoice[Table[1/w, {w, n}] -> names, {2, bugs}]]) // Short
Out[383]=

Create a pandas "DataFrame" object for the database:

In[384]:=
session = StartExternalSession["Python"]; pd = ResourceFunction["PandasObject"][session]; df = pd["DataFrame"[db]]
Out[384]=
In[385]:=
df["Head"[]] // Normal
Out[385]=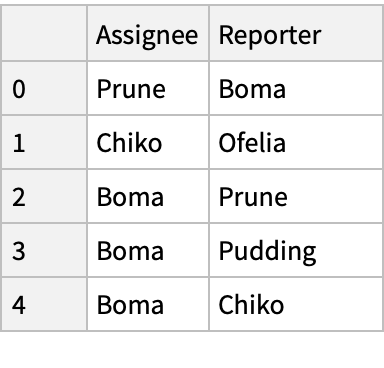

Construct a graph of the database:

In[386]:=
nx = ResourceFunction["NetworkXObject"][session]
Out[386]=
In[387]:=
g = nx["FromPandasEdgeList"[df, "Source" -> "Assignee", "Target" -> "Reporter"]]
Out[387]=

Team members Boma and Pudding are apparently in the center of action:

In[388]:=
Graph[g // Normal, VertexLabels -> Automatic]
Out[388]=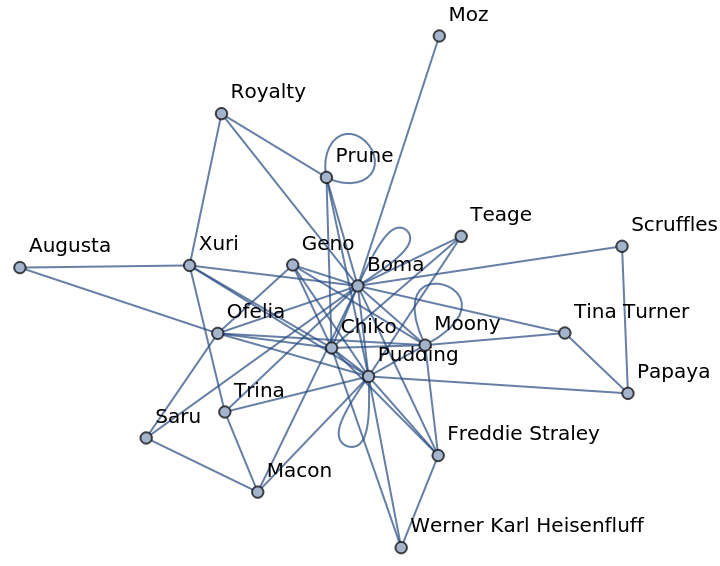

Extract all connections represented by edges of the graph:

In[389]:=
edges = g["Edges"] // Normal // Keys
Out[389]=

Create a table of participants sorted by activity:

In[390]:=
cnodes = List @@@ edges // Flatten;
In[391]:=
Take[SortBy[{#, Count[cnodes, #]} & /@ names, Last] // Reverse, 5] // Grid
Out[391]=
In[392]:=
DeleteObject[session]

Properties and Relations (9) 

NetworkXObject[…] gives the same result as the resource function PythonObject with a special configuration:

In[393]:=
session = StartExternalSession["Python"]; ResourceFunction["NetworkXObject"][session]
Out[393]=
In[394]:=
ResourceFunction["PythonObject"][session, "networkx", "Configuration" -> ResourceFunction["NetworkXObject"]]
Out[394]=
In[395]:=
DeleteObject[session]

Get information on a NetworkX object:

In[396]:=
nx = ResourceFunction["NetworkXObject"][]
Out[396]=
In[397]:=
nx["Information"] // Short
Out[397]=

Open the user guide in your default web browser:

In[398]:=
nx["WebInformation"] // SystemOpen
In[399]:=
DeleteObject[nx["Session"]]

Some of the functions and classes available in the NetworkX module:

In[400]:=
nx = ResourceFunction["NetworkXObject"][]; nx["FullInformation", "Functions"] // Short[#, 3] &
Out[400]=
In[401]:=
nx["FullInformation", "Classes"] // Short[#, 3] &
Out[401]=
In[402]:=
DeleteObject[nx["Session"]]

Information on a function:

In[403]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Information", "AdamicAdarIndex"]
Out[403]=

Web documentation of a function:

In[404]:=
nx["WebInformation", "AdamicAdarIndex"] // SystemOpen
In[405]:=
DeleteObject[nx["Session"]]

Functions similar to the given one; click the function name to go to the web documentation:

In[406]:=
nx = ResourceFunction["NetworkXObject"][]; nx["AdamicAdarIndex"]["Module"]
Out[406]=
In[407]:=
ResourceFunction["NetworkXObject"][nx, "Explore"["Functions", %]]
Out[407]=
In[408]:=
DeleteObject[nx["Session"]]

Aliases defined for a function or class:

In[409]:=
nx = ResourceFunction["NetworkXObject"][]; nx["Aliases", "BinomialGraph"]
Out[409]=
In[410]:=
nx["Aliases", "ErdosRenyiGraph"]
Out[410]=
In[411]:=
DeleteObject[nx["Session"]]

NetworkX Graph objects are analogous to Graph, but keep the objects on the Python side:

In[412]:=
g = \!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4}, {Null, SparseArray[ Automatic, {4, 4}, 0, {1, {{0, 3, 5, 6, 6}, {{1}, {2}, {3}, {3}, {4}, {4}}}, { 1, 1, 1, 1, 1, 1}}]}]]}, TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData[" 1:eJxTTMoPSmViYGCQBmIQbWXYLHHg/l/7lHsaT7qv3bZvXB8ZzPvorf0PyT06 itdf2+t1vFwSAuQzoIGdZSk1nkD1de5eDxge/LUX3Bei/1Dsjv2qbR5tU3j/ 2Z+V2M5v6fHAfv0p2ZD5nf/s32V2pFWFPLI/G8ViqOf1397M1bpOne2J/bWZ Qb3P5RkcsrrZ9MutntqvVJ2qlr6awYHBb+ukdTee2qvesMtKtWF0cNPivyJz 5an9lH2LOB2PMzp0CRw4Jq/71D7E7sLGaw5MDnHTNibIfHxsnznlz4HU+UwO m57Fr8+2fGSvY7y4I+I2k4Ma0/OIIM0H9gkNNjwP3jM5iGzNuBgBdP9ZzdJ9 YUD518FRf/mirtufvZQQmATUf6I6zvuR5WV7n/0hjy8Cze/3YFsvMvW8/b34 X3bWQPsrLs2NkF96yn7byjCpeKD7FipHX3fjPGHvFc91OQHo/ihlzlMy34/b W0rw7ngI9N+EM1G6YgWn7H8/mVikAvS/UsXXglzH8/b2qjc9ZwDDZ2FocZMU y2X7sjsHD0wAhh9/0IX4xTLX7dVLP68Bhe9i5cNTzabdtgcAYTq/8w== "], { {Hue[0.6, 0.7, 0.5], Opacity[0.7], {Arrowheads[0.], ArrowBox[BezierCurveBox[{1, 8, 11, 13, 19, 21, 24, 1}, SplineDegree->7], 0.021524138203359522`]}, {Arrowheads[0.], ArrowBox[{1, 2}, 0.021524138203359522`]}, {Arrowheads[0.], ArrowBox[{1, 3}, 0.021524138203359522`]}, {Arrowheads[0.], ArrowBox[{2, 3}, 0.021524138203359522`]}, {Arrowheads[0.], ArrowBox[{2, 4}, 0.021524138203359522`]}, {Arrowheads[0.], ArrowBox[{3, 4}, 0.021524138203359522`]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.021524138203359522], DiskBox[2, 0.021524138203359522], DiskBox[3, 0.021524138203359522], DiskBox[4, 0.021524138203359522]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FormatType->TraditionalForm, FrameTicks->None]\)
Out[412]=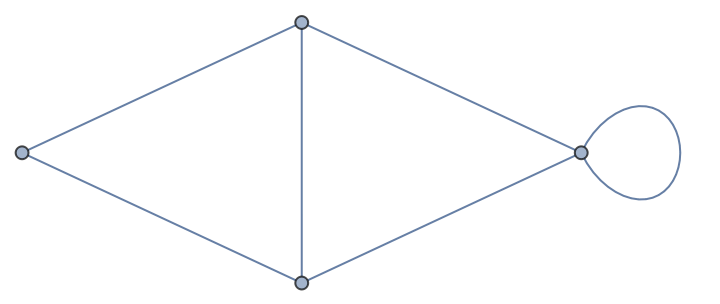
In[413]:=
nx = ResourceFunction["NetworkXObject"][]; ng = nx["Graph"[g]]
Out[413]=

Similarly, many graph properties and functions closely correspond to Wolfram Language functions:

In[414]:=
AssociationThread[VertexList[g] -> VertexDegree[g]] // KeySort
Out[414]=
In[415]:=
nx["Degree"[ng]] // Normal // KeySort
Out[415]=
In[416]:=
DeleteObject[nx["Session"]]

Functions of the same name might be defined in different modules:

In[417]:=
nx = ResourceFunction["NetworkXObject"][]
Out[417]=
In[418]:=
funs = nx["FullInformation", "Functions"];
In[419]:=
Cases[funs, _List]
Out[419]=

Functions defined for both general and bipartite graphs:

In[420]:=
Select[%, AnyTrue[#, Function[name, StringContainsQ[name, "Bipartite"]]] &]
Out[420]=
In[421]:=
DeleteObject[nx["Session"]]

Define a bipartite graph in the Wolfram Language and NetworkX:

In[422]:=
g = CompleteGraph[{2, 3}, VertexLabels -> Automatic]
Out[422]=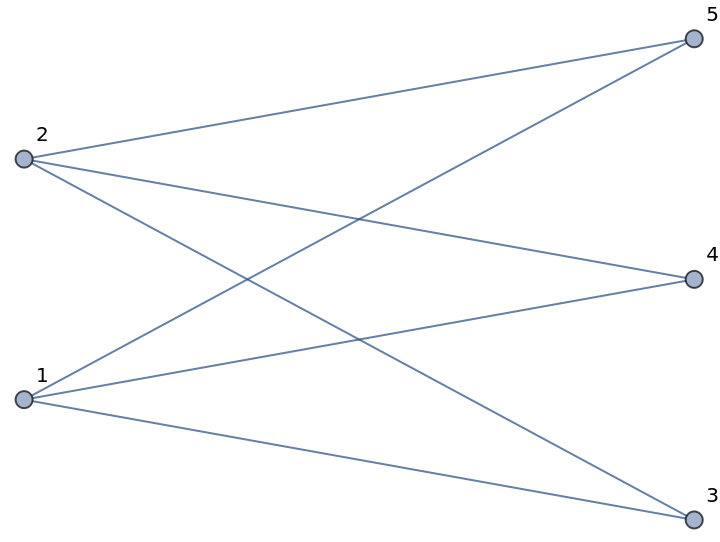
In[423]:=
nx = ResourceFunction["NetworkXObject"][]; ng = nx["Graph"[g]]
Out[423]=

The general function "ClosenessCentrality" function can be accessed by an unqualified name, returning the same values as the corresponding Wolfram Language function ClosenessCentrality:

In[424]:=
nx["ClosenessCentrality"[ng]] // KeySort
Out[424]=
In[425]:=
AssociationThread[VertexList[g] -> ClosenessCentrality[g]]
Out[425]=

Use a qualified name to access the bipartite version of the function:

In[426]:=
nx["Bipartite.ClosenessCentrality"[ng, {1, 2}]]
Out[426]=
In[427]:=
DeleteObject[nx["Session"]]

Possible Issues (4) 

NetworkX uses zero-based indexes, while the Wolfram Language Graph uses one-based node indexes:

In[428]:=
nx = ResourceFunction["NetworkXObject"][]; (m = SparseArray[{{0, 1, 0}, {1, 0, 1}, {0, 1, 0}}]) // MatrixForm
Out[428]=
In[429]:=
g = nx["Graph"[m]]
Out[429]=

See the vertex indexing from NetworkX:

In[430]:=
g["Nodes"] // Normal // Keys
Out[430]=

Compare with the default indexing in Graph:

In[431]:=
AdjacencyGraph[m] // VertexList
Out[431]=

Use "RelabelNodes" to index the nodes differently:

In[432]:=
nx["RelabelNodes"[g, <|0 -> 1, 1 -> 2, 2 -> 3|>]]
Out[432]=

Now the indices are identical:

In[433]:=
%["Nodes"] // Normal // Keys
Out[433]=
In[434]:=
DeleteObject[nx["Session"]]

When constructing graphs from Graph, NetworkXObject may not pass all annotations:

In[435]:=
g = PathGraph[Range[3], AnnotationRules -> {1 -> {VertexLabels -> "hello"}, 2 -> {VertexLabels -> "there"}}]
Out[435]=
In[436]:=
nx = ResourceFunction["NetworkXObject"][]; (ng = nx["Graph"[%]])["Nodes"] // Normal
Out[436]=

Use "SetNodeAttributes" to pass the annotations:

In[437]:=
AnnotationValue[g, VertexLabels]
Out[437]=
In[438]:=
nx["SetNodeAttributes"[ng, Association[%], "Name" -> "label"]]
In[439]:=
ng["Nodes"] // Normal
Out[439]=
In[440]:=
DeleteObject[nx["Session"]]

NetworkXObject choses the type of edges in graph constructors based on the graph type, effectively discarding the DirectedEdge and UndirectedEdge wrappers:

In[441]:=
nx = ResourceFunction["NetworkXObject"][]; (g = nx["DiGraph"[{1 \[DirectedEdge] 2, 2 \[UndirectedEdge] 3}]]) // Normal
Out[441]=
In[442]:=
g["Edges"] // Normal
Out[442]=

Similarly, the wrappers are discarded in all other functions:

In[443]:=
MemberQ[g["Edges"], 1 \[UndirectedEdge] 2] // Normal
Out[443]=
In[444]:=
DeleteObject[nx["Session"]]

An attempt to call a function by an unqualified name might fail if the function is defined in multiple contexts:

In[445]:=
nx = ResourceFunction["NetworkXObject"][]; nx["HavelHakimiGraph"[{3, 2, 2, 1, 0}, {3, 2, 2, 1, 0}]]
Out[445]=

Use a qualified name to call the bipartite version of the function:

In[446]:=
nx["Bipartite.HavelHakimiGraph"[{3, 2, 2, 1, 0}, {3, 2, 2, 1, 0}]]
Out[446]=
In[447]:=
Normal[%]
Out[447]=

Use an unqualified name to call the general function:

In[448]:=
g = nx["HavelHakimiGraph"[{3, 2, 2, 1, 0}]]
Out[448]=
In[449]:=
Normal[%]
Out[449]=
In[450]:=
DeleteObject[nx["Session"]]

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.0 – 01 March 2024

Source Metadata

  • Citation:
    • Aric A. Hagberg, Daniel A. Schult and Pieter J. Swart, "Exploring network structure, dynamics, and function using NetworkX", in Proceedings of the 7th Python in Science Conference (SciPy2008), Gäel Varoquaux, Travis Vaught, and Jarrod Millman (Eds), (Pasadena, CA USA), pp. 11–15, Aug 2008

Related Resources

Author Notes

The documentation created with:

In[1]:=
NetworkXObject[]["Version"]

Loading/caching some parts of the NetworkX package may take time, as seen by the "Amending…" temporary print. Until the resource function PythonObject amends the cache automatically, you can do it manually at any time after one or more of such long operations:

In[2]:=
DeleteObject[NetworkXObject["LocalCache" -> True]["Session"]]

As mentioned in Possible Issues, NetworkXObject currently simply discards the DirectedEdge and UndirectedEdge wrappers, the support for which is added merely as convenience, to facilitate, e.g., shipping the result of EdgeList[] to the nx["Graph"[…] constructor. If we want to be more robust (or more pedantic), we can add a form of type checking down the road.

Random graphs and some of the algorithms from the NetworkX package will be conveniently available using the NetworkXLink paclet when it is published in the Wolfram Language Paclet Repository.

License Information