Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NegativeCoordinateMarginalDistribution

Source Notebook

Represent a MarginalDistribution permitting negative numbers as indices

Contributed by: Seth J. Chandler

ResourceFunction["NegativeCoordinateMarginalDistribution"][dist,k]

represents a univariate marginal distribution of the kth coordinate from the multivariate distribution dist, where k is allowed to be a negative index.

ResourceFunction["NegativeCoordinateMarginalDistribution"][dist,{k1,k2,… }]

represents a multivariate marginal distribution of the {k1,k2,…} coordinates, but extending the coordinate values to permit negative indices.

ResourceFunction["NegativeCoordinateMarginalDistribution"][dist]

represents the last marginal distribution of the distribution dist.

Details

ResourceFunction["NegativeCoordinateMarginalDistribution"] determines the number of coordinates by considering the length of DistributionDomain applied to the distribution.
ResourceFunction["NegativeCoordinateMarginalDistribution"] can compute anything that MarginalDistribution can compute.

Examples

Basic Examples (2) 

Get the marginal distribution of a CategoricalDistribution for its last coordinate:

In[1]:=
ResourceFunction["NegativeCoordinateMarginalDistribution"][ CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 2}, {3, 4}, {5, 6}}], -1]
Out[1]=

Get the marginal distribution of a symbolic multivariate normal distribution for its penultimate coordinate:

In[2]:=
\[CapitalSigma] = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SuperscriptBox[ SubscriptBox["\[Sigma]", "1"], "2"], RowBox[{ SubscriptBox["\[Rho]", "12"], " ", SubscriptBox["\[Sigma]", "1"], " ", SubscriptBox["\[Sigma]", "2"]}], RowBox[{ SubscriptBox["\[Rho]", "13"], " ", SubscriptBox["\[Sigma]", "1"], " ", SubscriptBox["\[Sigma]", "3"]}]}, { RowBox[{ SubscriptBox["\[Rho]", "12"], " ", SubscriptBox["\[Sigma]", "1"], " ", SubscriptBox["\[Sigma]", "2"]}], SuperscriptBox[ SubscriptBox["\[Sigma]", "2"], "2"], RowBox[{ SubscriptBox["\[Rho]", "23"], " ", SubscriptBox["\[Sigma]", "2"], " ", SubscriptBox["\[Sigma]", "3"]}]}, { RowBox[{ SubscriptBox["\[Rho]", "13"], " ", SubscriptBox["\[Sigma]", "1"], " ", SubscriptBox["\[Sigma]", "3"]}], RowBox[{ SubscriptBox["\[Rho]", "23"], " ", SubscriptBox["\[Sigma]", "2"], " ", SubscriptBox["\[Sigma]", "3"]}], SuperscriptBox[ SubscriptBox["\[Sigma]", "3"], "2"]} }, GridBoxAlignment->{ "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\); \[ScriptCapitalD] = MultinormalDistribution[{Subscript[\[Mu], 1], Subscript[\[Mu], 2], Subscript[\[Mu], 3]}, \[CapitalSigma]];
In[3]:=
ResourceFunction[ "NegativeCoordinateMarginalDistribution"][\[ScriptCapitalD], -2]
Out[3]=

Scope (2) 

Positive and negative indices can be used together:

In[4]:=
ResourceFunction["NegativeCoordinateMarginalDistribution"][ MultinormalDistribution[{3, 4, 8}, {{5, -1, -2}, {-1, 3, 2}, {-2, 2, 6}}], {1, -1}]
Out[4]=

If no index is specified, the last index is used:

In[5]:=
ResourceFunction["NegativeCoordinateMarginalDistribution"][ MultinormalDistribution[{3, 4}, {{5, -1}, {-1, 6}}]]
Out[5]=

Applications (7) 

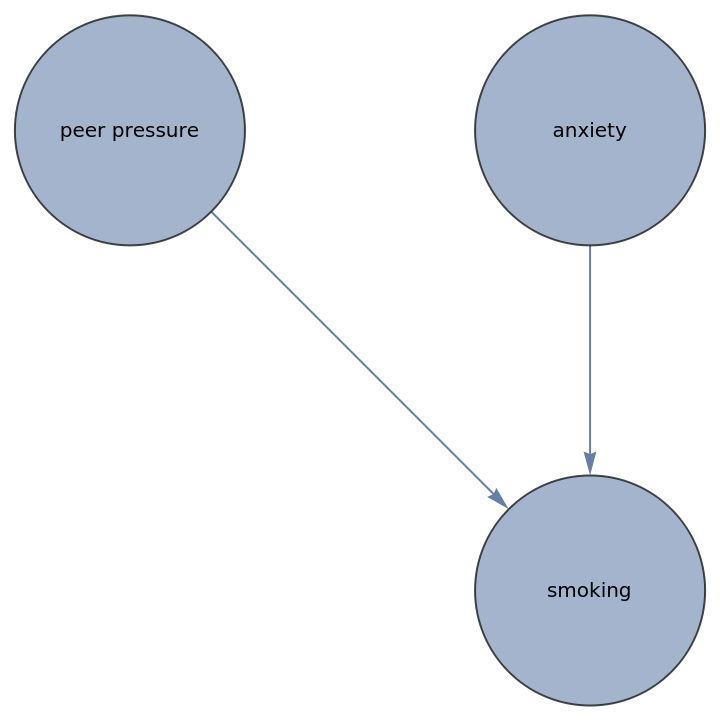
A causal graph between anxiety, peer pressure and smoking:

In[6]:=
Graph[{"peer pressure" \[DirectedEdge] "smoking", "anxiety" \[DirectedEdge] "smoking"}, VertexLabels -> Placed["Name", Center], VertexSize -> 0.5]
Out[6]=

Determine the effect of changing the probability of peer pressure on the probability of smoking as follows. First, generate categorical distributions for peer pressure and anxiety:

In[7]:=
peerDist = CategoricalDistribution[{"no peer pressure", "peer pressure"}, {1 - p, p}];
In[8]:=
anxietyDist = CategoricalDistribution[{"no anxiety", "anxiety"}, {3/10, 7/10}];

Assume the two are independent and so one can find their joint distribution using the resource function MixtureCategoricalDistribution as follows:

In[9]:=
mix = ResourceFunction[ ResourceObject[ Association[ "Name" -> "MixtureCategoricalDistribution", "ShortName" -> "MixtureCategoricalDistribution", "UUID" -> "3651811f-054b-490b-8d5a-4501b61f8f21", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Create a mixture distribution of categorical distributions and output it as a new CategoricalDistribution", "RepositoryLocation" -> URL[ "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$08a50866e9ab47568328ea27baaeac40`MixtureCategoricalDistribution", "FunctionLocation" -> CloudObject[ "https://www.wolframcloud.com/obj/9530a0ac-e8d9-4bc3-984f-00d791f46e80"]], ResourceSystemBase -> Automatic]][ anxietyDist, {peerDist, peerDist}]
Out[9]=

To use a CategoricalDistribution as input to another MixtureCategoricalDistribution, it must be univariate:

In[10]:=
univariateMix = CategoricalDistribution[ cat @@@ Tuples[Information[mix, "Categories"]], Flatten[Information[mix, "ProbabilityArray"]]]
Out[10]=

Now form the distribution of smoking as a function of whether the person is anxious and subject to peer pressure:

In[11]:=
smokeDist = ResourceFunction[ ResourceObject[ Association[ "Name" -> "MixtureCategoricalDistribution", "ShortName" -> "MixtureCategoricalDistribution", "UUID" -> "3651811f-054b-490b-8d5a-4501b61f8f21", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Create a mixture distribution of categorical distributions and output it as a new CategoricalDistribution", "RepositoryLocation" -> URL[ "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$08a50866e9ab47568328ea27baaeac40`MixtureCategoricalDistribution", "FunctionLocation" -> CloudObject[ "https://www.wolframcloud.com/obj/9530a0ac-e8d9-4bc3-984f-00d791f46e80"]], ResourceSystemBase -> Automatic]][ univariateMix, {CategoricalDistribution[{"no smoke", "smoke"}, {9/ 10, 1/10}], CategoricalDistribution[{"no smoke", "smoke"}, {7/10, 3/10}], CategoricalDistribution[{"no smoke", "smoke"}, {6/10, 4/10}], CategoricalDistribution[{"no smoke", "smoke"}, {2/10, 8/10}]}]
Out[11]=

Use NegativeCoordinateMarginalDistribution to get the probability of smoking as a function of the prevalence of peer pressure:

In[12]:=
smokingProbs = Information[ Echo@ResourceFunction["NegativeCoordinateMarginalDistribution"][ smokeDist, -1], "Probabilities"]
Out[12]=

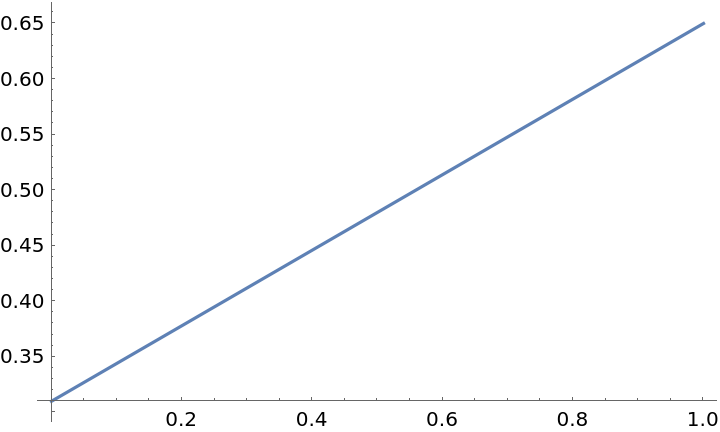
Plot the relationship between the prevalence of peer pressure and the probability of smoking:

In[13]:=
Plot[smokingProbs["smoke"], {p, 0, 1}]
Out[13]=

Properties and Relations (2) 

NegativeCoordinateMarginalDistribution works the same as MarginalDistribution if a positive number is used for the index:

In[14]:=
ResourceFunction["NegativeCoordinateMarginalDistribution"][ MultinormalDistribution[{3, 4}, {{5, -1}, {-1, 6}}], 2]
Out[14]=
In[15]:=
MarginalDistribution[ MultinormalDistribution[{3, 4}, {{5, -1}, {-1, 6}}], 2]
Out[15]=

NegativeCoordinateMarginalDistribution[dist] is equivalent to NegativeCoordinateMarginalDistribution[dist,-1]:

In[16]:=
\[ScriptCapitalD] = MultinormalDistribution[{3, 4}, {{5, -1}, {-1, 6}}]; ResourceFunction[ "NegativeCoordinateMarginalDistribution"][\[ScriptCapitalD]] === ResourceFunction[ "NegativeCoordinateMarginalDistribution"][\[ScriptCapitalD], -1]
Out[16]=

Publisher

Seth J. Chandler

Version History

  • 1.0.0 – 27 July 2021

Related Resources

License Information