Basic Examples (4)
Take two categorical distributions whose common domain is  and compose it with a categorical distribution whose domain is {"♂","♀"}:
and compose it with a categorical distribution whose domain is {"♂","♀"}:
Produce five random draws from the resulting distribution:
Represent the probabilities of the resulting distribution as an array:
Compute the entropy of the resulting distribution:
Scope (3)
Use a symbolic univariate CategoricalDistribution to create a new bivariate CategoricalDistribution from two components that are themselves symbolic univariate categorical distributions:
See the probability values:
The function works when the components are multivariate:
See the probability values:
The function can be nested:
Applications (1)
In some nation, 70% of the people prefer looking at Mars (♂) and 30% of the people prefer looking at Venus (♀). Among Mars supporters, 6 out of 10 prefer the "Wolf" soccer team and 4 out of 10 prefer the "Bulb" soccer team. Among Venus supporters, 7 out of 20 prefer the "Wolf" and 13 out of 20 prefer the "Bulb". What is the joint distribution of planetary preference and favorite soccer team?
Now assume a crowd of one thousand randomly selected individuals from the nation attend a game. Compute the probability that the majority will be Bulb fans:
Properties and Relations (3)
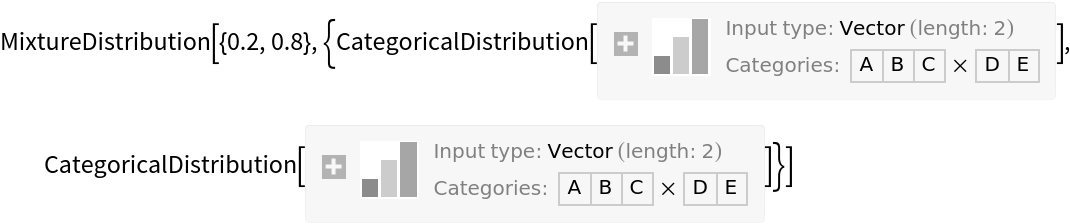
One can construct a mixture of CategoricalDistribution objects using the MixtureDistribution function, but many desired properties of a distribution are not presently available:
The following code, for example, attempts to get the probability of the mixture returning {"A","E"} and producing two random variables from the mixture. Neither effort succeeds:
By contrast, when one uses MixtureCategoricalDistribution, the same sort of information can be successfully obtained:
Possible Issues (1)
The function returns $Failed if the domains of the components are not identical:
Neat Examples (1)
Here is an example from the Wikipedia entry for the Bayes theorem. "A particular test for whether someone has been using marijuana is 90% sensitive and 80% specific, meaning it leads to 90% true 'positive' results (meaning, 'Yes, he used marijuana') for marijuana users and 80% true negative results for non-users—but also generates 20% false positives for non-users. Only 5% of people actually do use marijuana. What is the probability that a random person who tests positive is really a drug user?" This can be solved in a clear fashion using MixtureCategoricalDistribution:
![]() and compose it with a categorical distribution whose domain is {"♂","♀"}:
and compose it with a categorical distribution whose domain is {"♂","♀"}:

![cd1 = CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 2}, {3, 4}, {5, 6}}];
cd2 = CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 5}, {2, 4}, {9, 2}}];
ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"\[Mars]", "\[Venus]"}, {a, b}], {cd1, cd2}]](https://www.wolframcloud.com/obj/resourcesystem/images/365/3651811f-054b-490b-8d5a-4501b61f8f21/0a0929ee905a69d4.png)

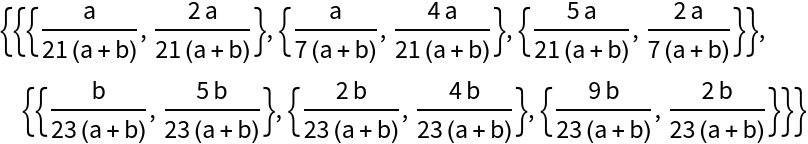
![ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"x", "y", "z"}, {0.2, 0.7, 0.1}], {ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"\[Mars]", "\[Venus]"}, {a, b}], {cd1, cd2}],
ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"\[Mars]", "\[Venus]"}, {c, d}], {cd1, cd2}], ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"\[Mars]", "\[Venus]"}, {e, f}], {cd1, cd2}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/365/3651811f-054b-490b-8d5a-4501b61f8f21/5c1ced0013731009.png)

![SurvivalFunction[
BinomialDistribution[1000, Query["\[LightBulb]"][
Information[MarginalDistribution[soccerDistribution, 2], "Probabilities"]]], 501] // N](https://www.wolframcloud.com/obj/resourcesystem/images/365/3651811f-054b-490b-8d5a-4501b61f8f21/26b81e53c51d8a0d.png)
![conventionalMixture = MixtureDistribution[{0.2, 0.8}, {CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 2}, {3, 4}, {5, 6}}],
CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 5}, {2,
4}, {9, 2}}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/365/3651811f-054b-490b-8d5a-4501b61f8f21/32aafd152f396573.png)

![mcd = ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"\[Mars]", "\[Venus]"}, {0.2, 0.8}], {CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 2}, {3, 4}, {5, 6}}],
CategoricalDistribution[{{"A", "B", "C"}, {"D", "E"}}, {{1, 5}, {2,
4}, {9, 2}}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/365/3651811f-054b-490b-8d5a-4501b61f8f21/78e3cae5a0340aca.png)

![population = ResourceFunction["MixtureCategoricalDistribution"][
CategoricalDistribution[{"users", "nonusers"}, {0.05, 0.95}], {CategoricalDistribution[{"negative", "positive"}, {0.1, 0.9}], CategoricalDistribution[{"negative", "positive"}, {0.8, 0.2}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/365/3651811f-054b-490b-8d5a-4501b61f8f21/5156bf573c9ccc51.png)
