Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NSeries

Source Notebook

Find a numerical approximation of a series expansion of a function

Contributed by: Wolfram Research

ResourceFunction["NSeries"][f,{x,x0,n}]

gives a numerical approximation to the series expansion of f about the point x=x0 including the terms (x-x0)-n through (x-x0)n.

Details and Options

The function f must be numeric when its argument x is numeric.
ResourceFunction["NSeries"] will construct standard univariate Taylor or Laurent series.
ResourceFunction["NSeries"] samples f at points on a circle in the complex plane centered at x0 and uses InverseFourier. The option "Radius" specifies the radius of the circle.
The region of convergence will be the annulus (containing the sampled points) where f is analytic.
ResourceFunction["NSeries"] will not return a correct result if the disk centered at x0 contains a branch cut of f.
The result of ResourceFunction["NSeries"] is a SeriesData object.
If the result of ResourceFunction["NSeries"] is a Laurent series, then the SeriesData object is not a correct representation of the series, as higher-order poles are neglected.
No effort is made to justify the precision in each of the coefficients of the series.
ResourceFunction["NSeries"] is unable to recognize small numbers that should in fact be zero. Chop is often needed to eliminate these spurious residuals.
The number of sample points chosen is 2Ceiling[Log[2,n]]+1.
The following options can be given:
"Radius"1radius of circle on which f is sampled
WorkingPrecisionMachinePrecisionprecision used in internal computations

Examples

Basic Examples (3) 

This is a power series for the exponential function around x=0:

In[1]:=
ResourceFunction["NSeries"][Exp[x], {x, 0, 5}]
Out[1]=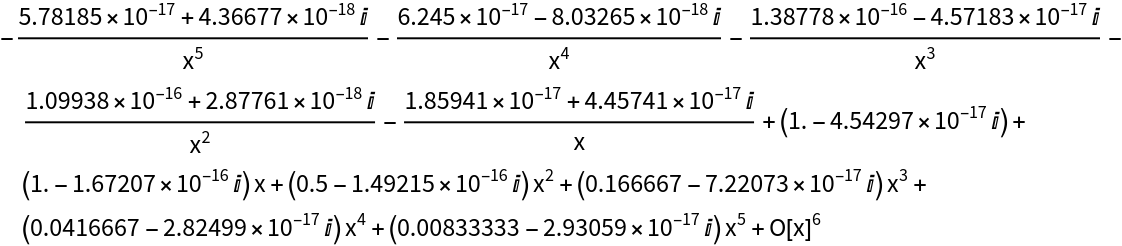

Chop is needed to eliminate spurious residuals:

In[2]:=
% // Chop
Out[2]=

Using extended precision may also eliminate spurious imaginaries:

In[3]:=
ResourceFunction["NSeries"][Exp[x], {x, 0, 5}, WorkingPrecision -> 17]
Out[3]=

Scope (2) 

Find expansions in the complex plane:

In[4]:=
ResourceFunction["NSeries"][Exp[x], {x, I, 5}] // Chop
Out[4]=

Find Laurent expansions about essential singularities:

In[5]:=
ResourceFunction["NSeries"][Sin[x + 1/x], {x, 0, 10}] // Chop
Out[5]=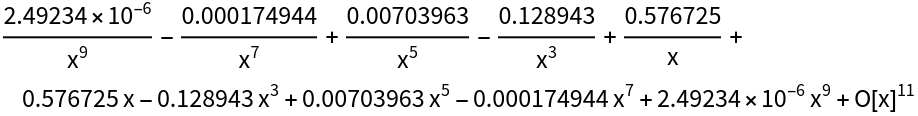

Series will not find Laurent expansions about essential singularities:

In[6]:=
Series[Sin[x + 1/x], {x, 0, 10}]
Out[6]=

Options (2) 

Radius (2) 

Use "Radius" to pick the annulus within which the Laurent series will converge:

In[7]:=
ResourceFunction["NSeries"][1/((1 + x) (3 + x)), {x, 0, 10}, "Radius" -> 2] // Chop
Out[7]=

Laurent series for x≥3:

In[8]:=
ResourceFunction["NSeries"][1/((1 + x) (3 + x)), {x, 0, 10}, "Radius" -> 5] // Chop
Out[8]=

Changing "Radius" can improve accuracy:

In[9]:=
ResourceFunction["NSeries"][1/(1 - x), {x, 0, 10}, "Radius" -> 7/8] // Chop
Out[9]=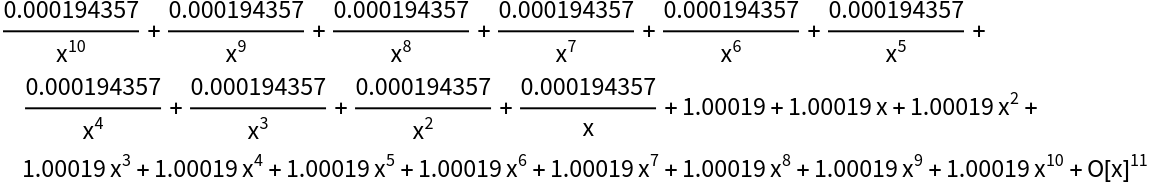
In[10]:=
ResourceFunction["NSeries"][1/(1 - x), {x, 0, 10}, "Radius" -> 1/5] // Chop
Out[10]=

Applications (3) 

A function defined only for numerical input:

In[11]:=
f[a_?NumericQ] := NIntegrate[Sin[a Sin[x] + Cos[x]], {x, 0, a}]

Find a series expansion of f:

In[12]:=
g[a_] = Normal@ResourceFunction["NSeries"][f[a], {a, 0, 10}] // Chop
Out[12]=

Check:

In[13]:=
Plot[{f[a], g[a]}, {a, 0, 2}]
Out[13]=

Properties & Relations (2) 

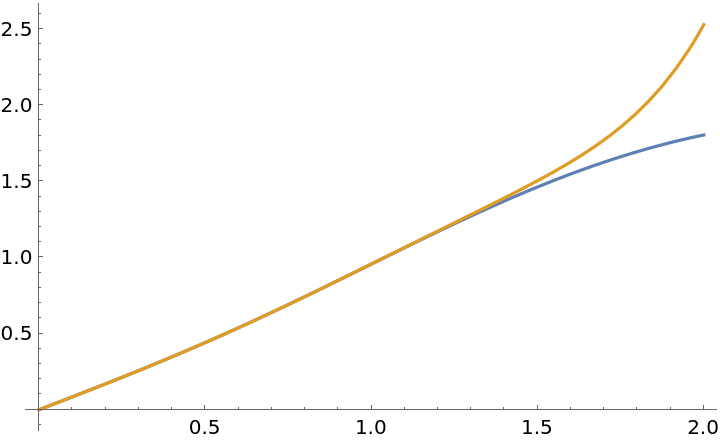NResidue can also be used to construct a series of a numerical function:

In[14]:=
f[x_?NumericQ] := Exp[x]
In[15]:=
ResourceFunction["NSeries"][f[x], {x, 0, 5}] // Chop
Out[15]=

Using NResidue:

In[16]:=
ResourceFunction["NResidue"][f[x] x^Range[-1, -6, -1], {x, 0}, "Radius" -> 1] . x^Range[0, 5] // Chop
Out[16]=

Possible Issues (2) 

NSeries can have aliasing problems due to InverseFourier:

In[17]:=
ResourceFunction["NSeries"][ArcSin[x], {x, 0, 20}] // Chop
Out[17]=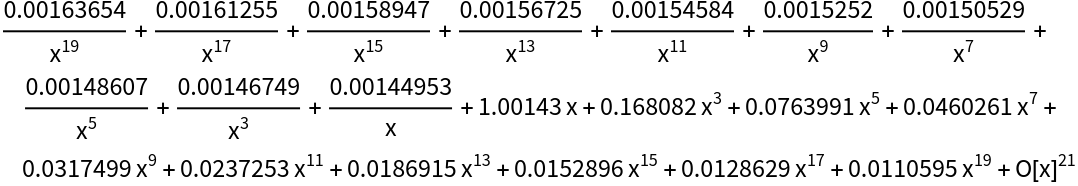

The correct expansion is analytic at the origin:

In[18]:=
Series[ArcSin[1. x], {x, 0, 20}]
Out[18]=

SeriesData cannot correctly represent a Laurent series. Here is the square of the series of :

In[19]:=
ResourceFunction["NSeries"][Exp[1/x + x], {x, 0, 5}]^2 // Chop
Out[19]=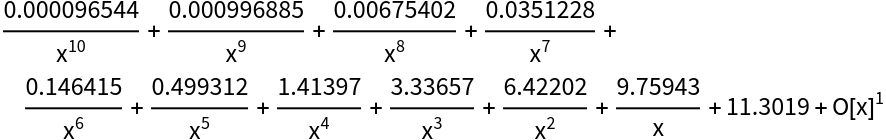

Here is the SeriesData representation of the Laurent series of :

In[20]:=
ResourceFunction["NSeries"][Exp[1/x + x]^2, {x, 0, 5}] // Chop
Out[20]=

Neat Examples (2) 

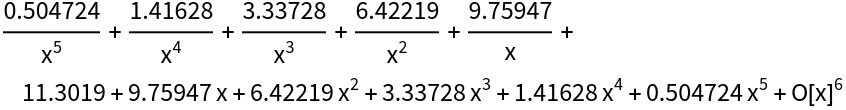Find the series expansion of the generating function for unrestricted partitions:

In[21]:=
q[z_?NumericQ] := NProduct[1/(1 - z^n), {n, \[Infinity]}]
In[22]:=
ResourceFunction["NSeries"][q[z], {z, 0, 20}, "Radius" -> 1/2, WorkingPrecision -> 17] // Chop
Out[22]=

Check:

In[23]:=
PartitionsP[Range[0, 20]]
Out[23]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 13 March 2019

Related Resources

License Information