Function Repository Resource:

MutualInformation

Source Notebook

Compute the mutual information of data samples or a multivariate distribution

Contributed by: Luigi Brancati

ResourceFunction["MutualInformation"][list₁,list₂]

estimates the mutual information of two lists of elements.

ResourceFunction["MutualInformation"][list,t]

estimates the auto-mutual information of list, comparing batches of elements at shifts given by Range[0, t].

ResourceFunction["MutualInformation"][list,{t,s}]

estimates the auto-mutual information, comparing running batches of length t at a fixed shift s.

ResourceFunction["MutualInformation"][dist]

computes the mutual information of a bivariate distribution dist.

ResourceFunction["MutualInformation"][dist_x,disty_y]

computes the mutual information of the bivariate distribution CopulaDistribution["Product",{dist_x,dist_y}].

Details and Options

The function ResourceFunction["MutualInformation"][dist] expects a bivariate or multivariate distribution.

The estimator ResourceFunction["MutualInformation"][list,t] computes the mutual information between list[i] and list[i+s], with s=1,2,…,t.

The function ResourceFunction["MutualInformation"][list,___] uses parallel kernels by default. To force sequential execution, use the option value "Parallelize"→False.

ResourceFunction["MutualInformation"][list,{t,0}] is equivalent to ResourceFunction["MutualInformation"][list,t].

The functions ResourceFunction["MutualInformation"][dist] and ResourceFunction["MutualInformation"][dist_x,dist_y] both rely on the KullbackLeiblerDivergence resource function to work, hence both accept the same options as KullbackLeiblerDivergence.

In addition to the options for KullbackLeiblerDivergence, the function ResourceFunction["MutualInformation"], when used on distributions, accepts the following options:

"CopulaKernel"

"Product"

uses the specified copula kernel to compute the joint distribution from the provided marginals

"Marginals"

Automatic

specifies how to extract marginals from the joint distribution

The option setting "Marginals"→Automatic splits the joint space in half.

Any kernel supported by CopulaDistribution can be provided, though some copulas will be hard to compute exactly. Use the option Method→NExpectation to compute a numerical approximation, which is much faster most of the time.

When used on lists of samples, the function ResourceFunction["MutualInformation"] accepts the following options:

DistanceFunction

ChessboardDistance

distance used to compute the estimator

"Errors"

False

whether or not to compute the error on the estimator

"KNeighbour"

kth-nearest neighbor parameter to be used for the estimator on lists of samples

"Parallelize"

True

whether or not to use parallel computation

ResourceFunction["MutualInformation"][list,___] uses an estimator that relies on a k^th-nearest neighbors algorithm (see Autor Notes). The default value of k is 4; to set a different value, use the option "KNeighbour".

The estimator performs poorly on very skewed distributions. In such cases, one should renormalize the distribution with Standardize to get better results.

Examples

Basic Examples (4)

Compute the mutual information of a binormal distribution:

In[1]:=

Out[1]=

Compare the result to its real value:

In[2]:=

Out[2]=

The same information can be computed using a symbolic distribution, too:

In[3]:=

$ResourceFunction["MutualInformation"][BinormalDistribution[\[Rho]]]$

Out[3]=

Compute the mutual information of a multivariate distribution (note: N is used to speed up the computation; see "Author Notes"):

In[4]:=

Out[4]=

Compute the mutual information of a bivariate distribution, starting from the two marginal distributions:

In[5]:=

Out[5]=

Estimate the mutual information between two samples, with errors:

In[6]:=

In[7]:=

Out[7]=

Options (6)

DistanceFunction (2)

Compute the mutual information between two sets of data, using any distance function:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

If no DistanceFunction is specified, the default is ChessboardDistance:

In[10]:=

In[11]:=

Out[11]=

In[12]:=

Out[12]=

In[13]:=

Out[13]=

Any kind of element in a List can be fed to the estimator:

In[14]:=

v1 = VideoExtractFrames[Video["ExampleData/Caminandes.mp4"], Quantity[Range[50, 100], "Frames"]];
v2 = VideoExtractFrames[Video["ExampleData/Caminandes.mp4"], Quantity[Range[100, 150], "Frames"]];

In[15]:=

Out[15]=

Errors (1)

Say whether you want to compute errors on the estimator (not available on distributions):

In[16]:=

Out[16]=

Marginals (2)

Note: the examples of this section may take several minutes to run. This is due to a bug that prevents one from using option Method→NExpectation, which should be preferred for multivariate distributions. See the Author Notes at the end of the notebook for more information.

Specify how to extract marginals from a multivariate distribution:

In[17]:=

$\[ScriptCapitalD] = MultinormalDistribution[{1, 2, 3}, {{2, 1/2, -1/3}, {1/2, 1, 0}, {-1/3, 0, 2/3}}];$

In[18]:=

$ResourceFunction["MutualInformation"][\[ScriptCapitalD], "Marginals" -> {1, 2}]$

Out[18]=

Notice that different ways to extract marginals are not equivalent:

In[19]:=

$ResourceFunction["MutualInformation"][\[ScriptCapitalD], "Marginals" -> {1, 3}]$

Out[19]=

CopulaKernel (1)

The option "CopulaKernel" is only available for MutualInformation[dist_x,dist_y]. It uses CopulaDistribution["CopulaKernel",{dist_x,dist_y}] as the joint distribution:

In[20]:=

Out[20]=

Applications (1)

Compute the mutual information shared between the initial and subsequent frames of a video:

In[21]:=

In[22]:=

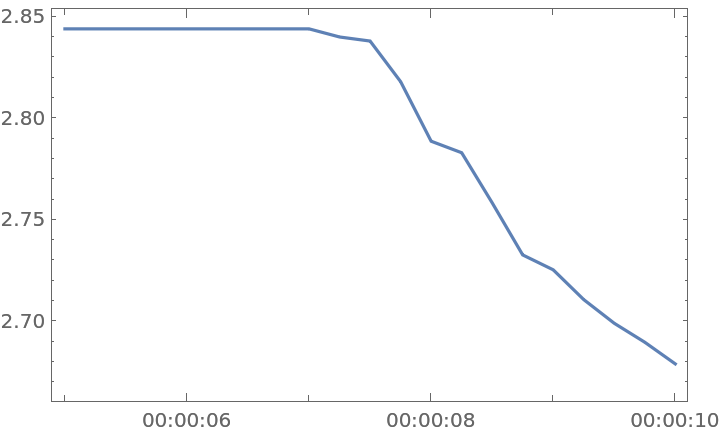
timeseries = TimeSeries[
ResourceFunction["MutualInformation"][videoframes, 20, DistanceFunction -> ImageDistance], {5, 10}];

In[23]:=

Out[23]=

Publisher

Wolfram Summer School

Version History

2.0.0 – 12 August 2020
1.0.0 – 10 August 2020

Source Metadata

Citation:
- Kraskov, A., Stoegbauer, H., Grassberger, P., "Estimating Mutual Information." arXiv preprint, 2003. https://arxiv.org/abs/cond-mat/0305641
- Holmes, C. M., Nemenman, I., "Estimation of mutual information for real-valued data with error bars and controlled bias. Phys. Rev. E, vol. 100, 022404, 2019.
- Vollmer, M., Rutter, I., Böhm, K., "On Complexity and Efficiency of Mutual Information Estimation on Static and Dynamic Data." Open Proceedings, 2018. DOI: 10.5441/002/edbt.2018.06

Related Resources

Author Notes

MutualInformation[list,___] uses an estimator which relies on a k-nearest neighbours algorithm (see [1]). The default value of k is 4, to set a different value use the option "KNeighbour"→value.

The estimator MutualInformation[list,___] performs poorly on very skewed distributions. Since the mutual information is invariant under smooth transformations of the joint space, one should renormalize the distribution with Standardize, or even transform the distributions into more uniform ones. For more details, see [1].

The estimator MutualInformation[list,___] is quite slow due to the amount of distances that needs to be computed, it has at the very best complexity of nLog(n) with n the size of the input list(s) (see [3]).

Using custom distances or any distance apart from the default ChessboardDistance slows down the computation significantly.

The computation of errors on MutualInformation[list,___] works by performing a sub-sampling procedure on the data provided, since other methods have been found to be inadequate (see [2]). This requires to compute the mutual information on smaller samples multiple times, which slows down the computation.

Most multivariate distributions will take a long time to compute exactly, so it is advised to use the option Method→NExpectation to perform a numeric approximation (this option is provided by KullbackLeiblerDivergence). Unfortunately, at the moment a bug in a key function used by MutualInformation[dist,dist] prevents the use of NExpectation as an option value, so it is advised to run N on parameter distributions to speed up the computation, as can be seen in section "Basic Examples".

Mutual Information is always positive, but it may happen that the estimator MutualInformation[list,___] gives back negative values, especially for weakly correlated data or too few data points. The estimator itself is asymptotically unbiased, so on large datasets its value doesn't depend on the specific distance used or on the value of "KNeighbour".

I would like to extend it to TimeSeries.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License