Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Plot multispace in 3D
ResourceFunction["MultispacePlot3D"][mwf] returns a visualization of multispace for multiway function mwf. | |
ResourceFunction["MultispacePlot3D"][mwf,prop] returns the property prop involved in computing a visualization of multispace. |
| "RawGraphs" | return a list of 2D graphs without computing a 3D embedding |
| "Association" | an Association returned by an underlying algorithm |
| "Graph" | GraphPlot3D of a multispace |
| "View" | Graphics3D with convenient controls (default) |
Return raw graphs of a multiway system:
| In[1]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwaySystem"][{"A" -> "AB", "B" -> "A"}, {"A"}, 6, ##] &, "RawGraphs"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/2533b436f6cf327e.png) |
| Out[1]= | 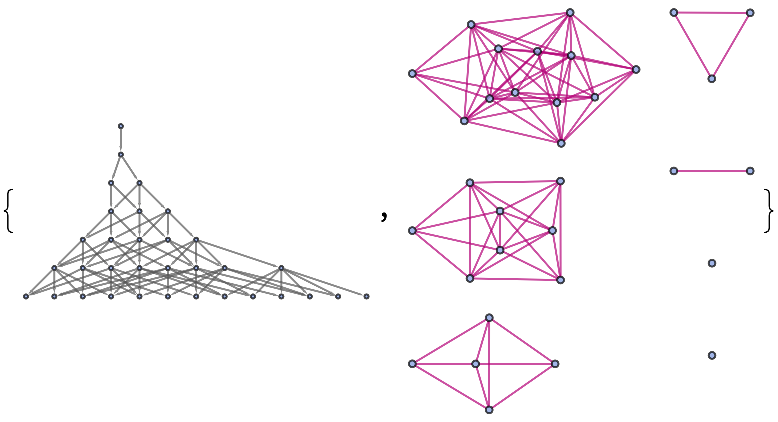 |
Return an Association with the results of an embedding algorithm:
| In[2]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwaySystem"][{"A" -> "AB", "B" -> "A"}, {"A"}, 6, ##] &, "Association"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/5927b77fdfb90664.png) |
| Out[2]= |  |
Return 3D graphics for a resulting Graph:
| In[3]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwayTuringMachine"][{1507, 2506, 3506}, {{1, 1, 0}, {0, 1, 0, 1}}, 4, ##] &, "Graph"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/714536e6f94467c4.png) |
| Out[3]= | 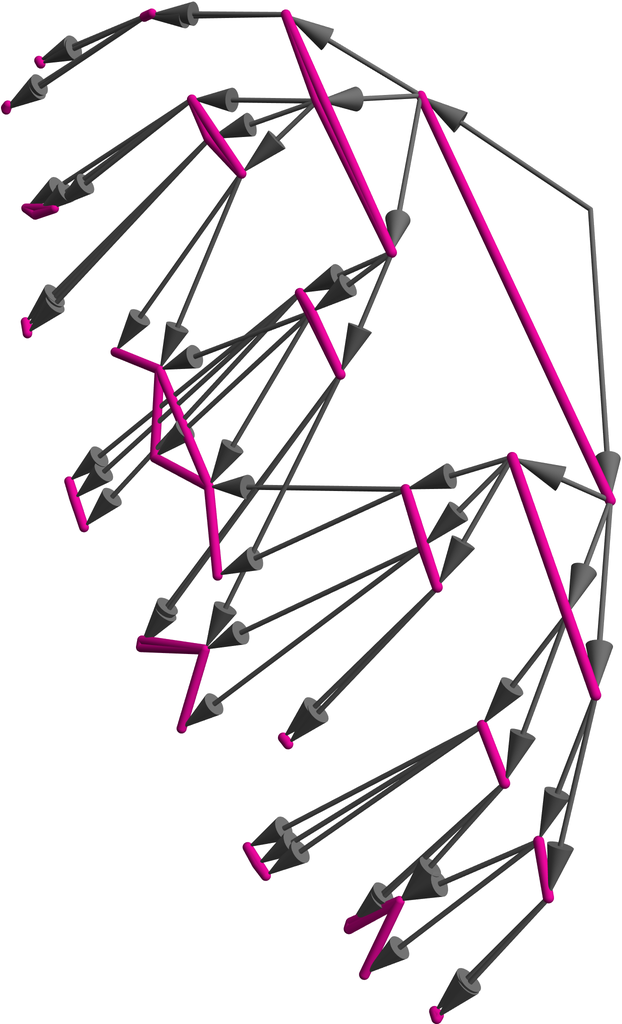 |
Add multiperspective controls to view the resulting Graph:
| In[4]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwayTuringMachine"][{1507, 2506, 3506}, {{1, 1, 0}, {0, 1, 0, 1}}, 4, ##] &, "View"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/2815cd05373824eb.png) |
| Out[4]= | 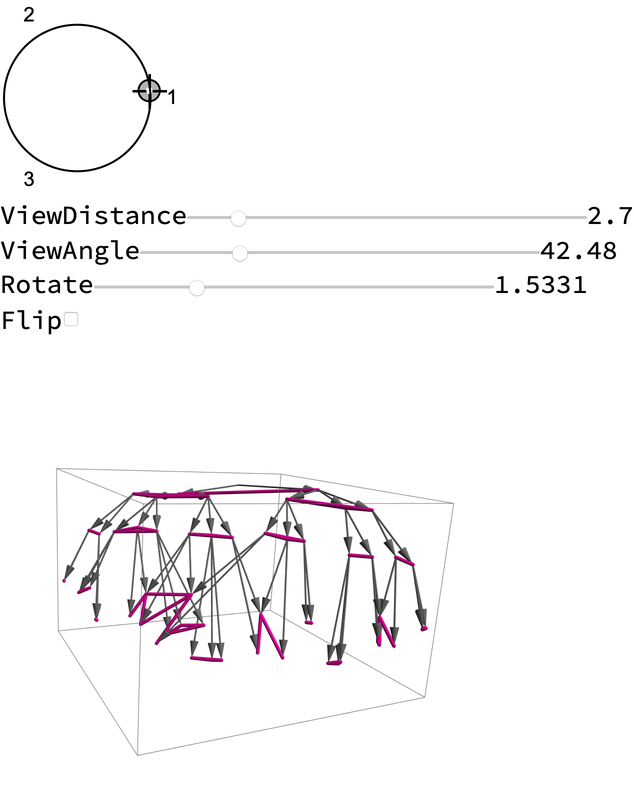 |
Plot the multispace of a Turing machine for events:
| In[5]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwayTuringMachine"][{1507, 2506, 3506}, {{1, 1, 0}, {0, 1, 0, 1}}, 4, ##] &, "RawGraphs", "ObjectType" -> "Event"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/74fdc3300a0f2b26.png) |
| Out[5]= | 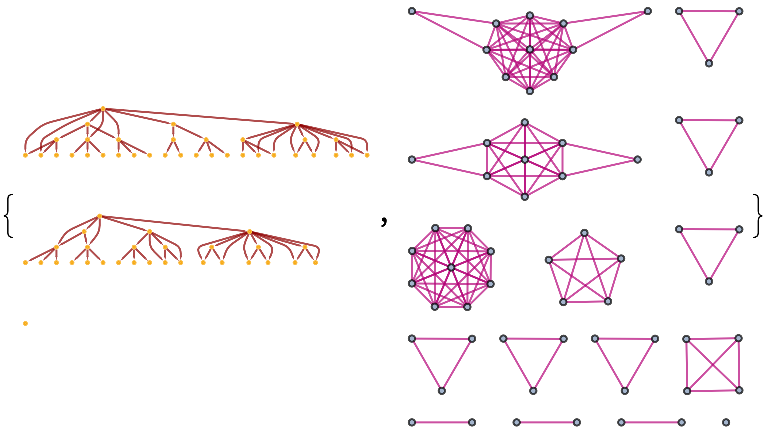 |
Or in 3D:
| In[6]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwayTuringMachine"][{1507, 2506, 3506}, {{1, 1, 0}, {0, 1, 0, 1}}, 4, ##] &, "ObjectType" -> "Event"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/57b3565677d61d58.png) |
| Out[6]= | 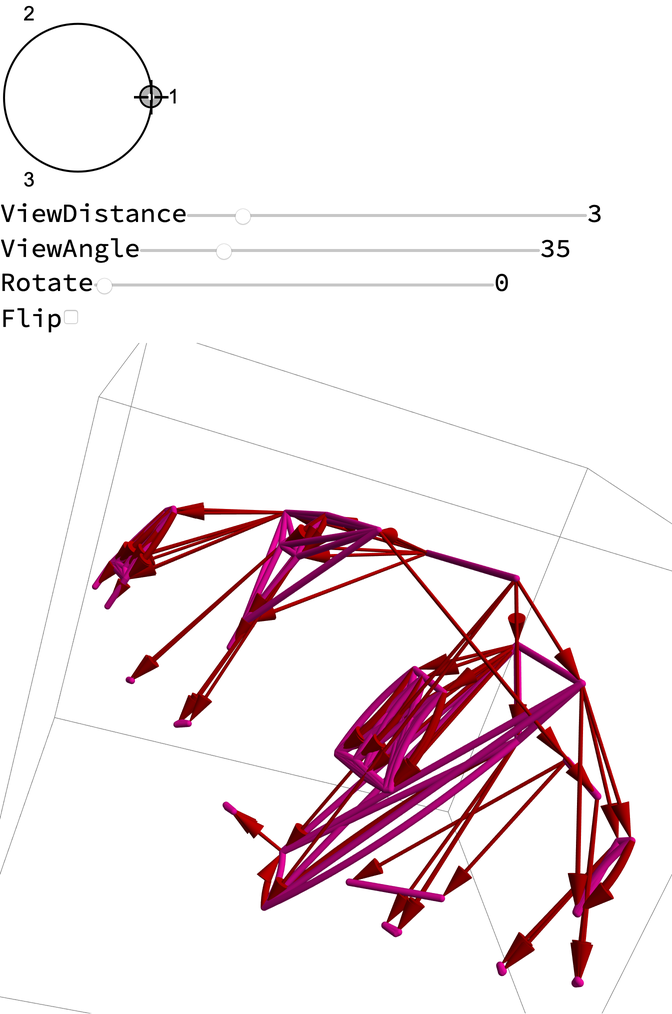 |
Increase distance between branchially disconnected states:
| In[7]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwaySystem"][{"A" -> "AB", "B" -> "A"}, {"A"}, 6, ##] &, "Graph", "InfiniteDistanceIncrement" -> 100]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/40a0a8a93d929b45.png) |
| Out[7]= |  |
Weights are constant multipliers of distances after normalization. In order, they are {time, space, branchial space}:
| In[8]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwaySystem"][{"A" -> "AB", "B" -> "A"}, {"A"}, 6, ##] &, "Graph", "DistanceMatrixWeights" -> {1, 1, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/0b69c4b808766a2c.png) |
| Out[8]= | 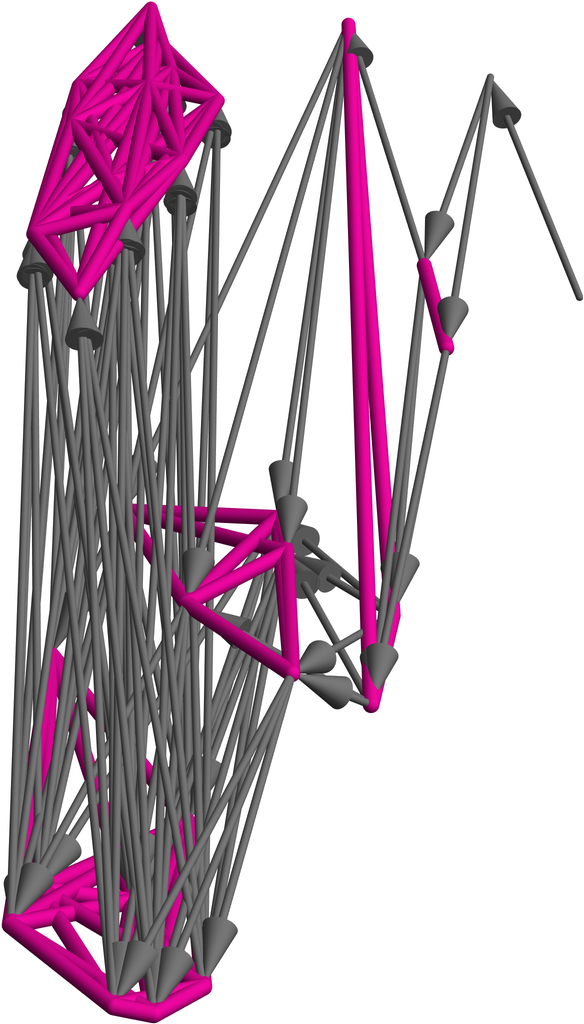 |
Options can be passed to the underlying algorithm:
| In[9]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwaySystem"][{"A" -> "AB", "B" -> "A"}, {"A"}, 6, ##] &, "Association", "TrainingProgressReporting" -> "Verbose"]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/07f27eb21fdb6a8f.png) |
| Out[9]= |  |
Or to the resulting Graphics3D object:
| In[10]:= | ![ResourceFunction["MultispacePlot3D"][
ResourceFunction["MultiwaySystem"][{"A" -> "AB", "B" -> "A"}, {"A"}, 6, ##] &, "Graph", ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/09d/09dd4cf5-1b91-4cb1-b0bd-7333821f1201/562ed75b32f0336d.png) |
| Out[10]= | 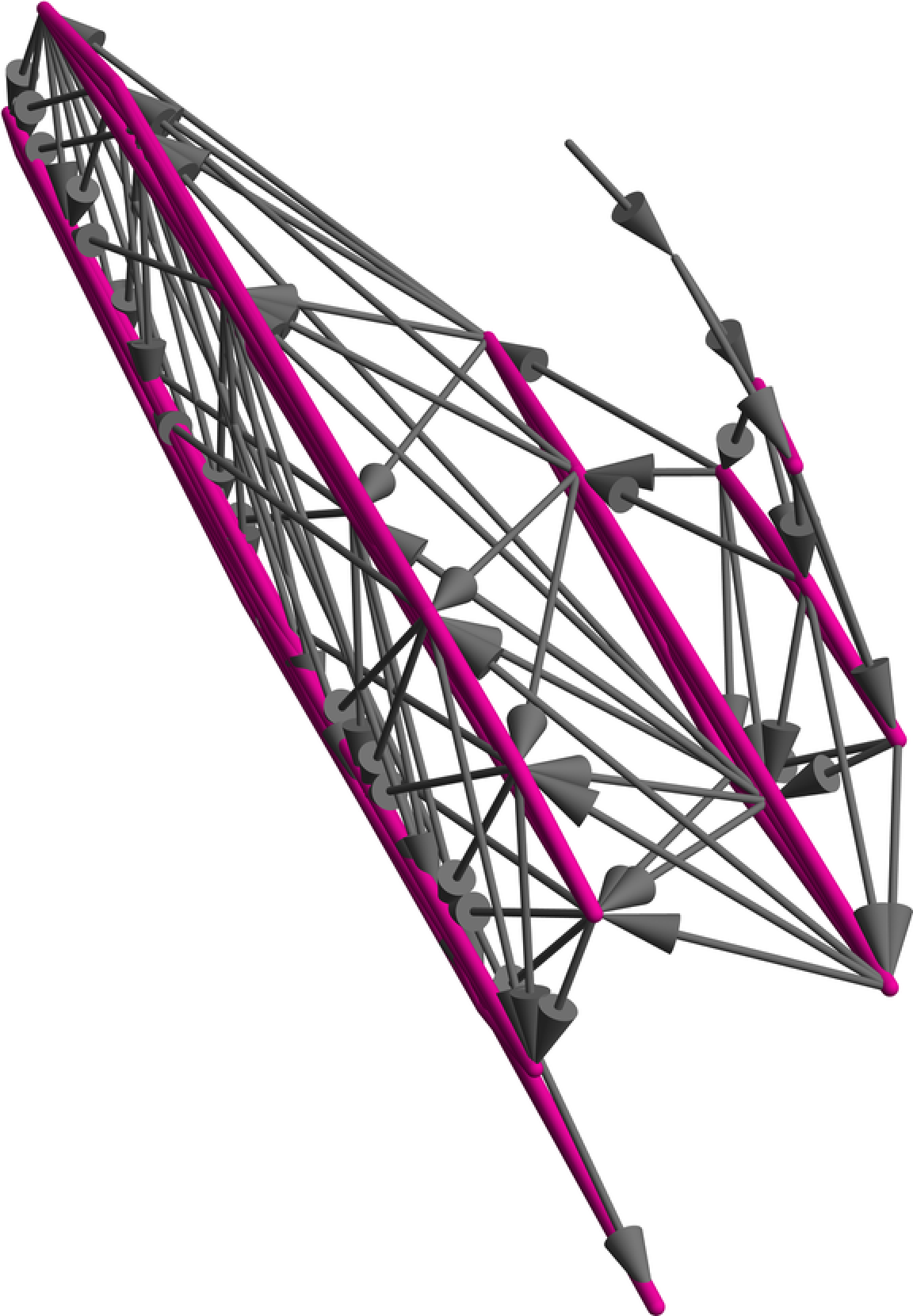 |
This work is licensed under a Creative Commons Attribution 4.0 International License