Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
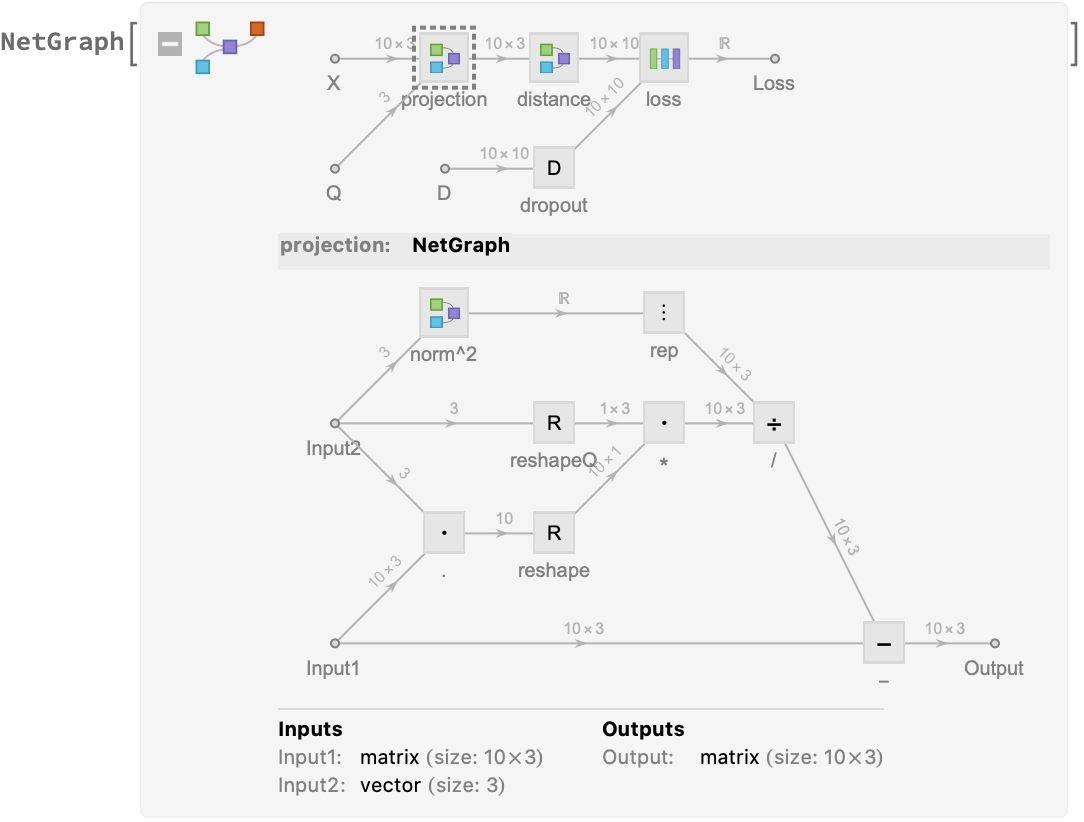
Compute a 3D embedding for multiple graphs so that all pairwise distances are preserved simultaneously along various 2D projections
ResourceFunction["MultiPerspectiveEmbedding"][gs] gives multi-perspective 3D embedding of graphs gs. | |
ResourceFunction["MultiPerspectiveEmbedding"][ds] gives multi-perspective 3D embedding for explicit distance matrices. |
| "InitialEmbedding" | Automatic | array of initial embedding vectors |
| "InitialProjection" | Automatic | array of initial normal vectors |
| "FixProjection" | False | whether to fix or learn projection vectors |
| "UseGraphEmbedding" | True | if the input is graphs, whether to use its embeddings for computing distances |
| "NormalizeDistances" | True | whether to normalize distances |
| "NetTrainOptions" | {} | custom options for NetTrain |
| TrainingProgressReporting | Automatic | use "Verbose" for custom reporting |
Compute a 3D embedding for a grid graph and a path graph:
| In[1]:= |
|
| Out[1]= |

|
Define larger grid and path graphs and show them:
| In[2]:= |
![With[{n = 8},
g1 = GridGraph[{n, n}, VertexLabels -> Automatic];
g2 = Graph[VertexList[g1], DirectedEdge @@@ Partition[
Catenate@
MapAt[Reverse, Partition[Range[n^2], n], List /@ Range[2, n, 2]], 2, 1], VertexCoordinates -> GraphEmbedding[g1], VertexLabels -> Automatic]
];
GraphicsRow[{g1, g2}]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/42edc4b23230152b.png)
|
| Out[3]= |
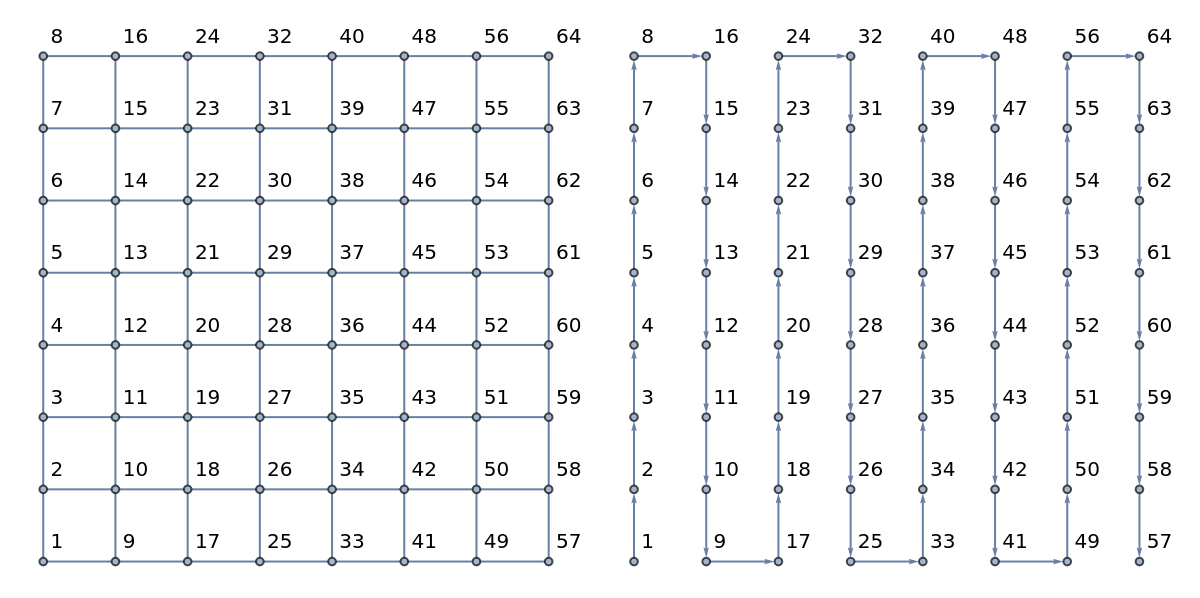
|
Compute an embedding:
| In[4]:= |
|
| Out[4]= |

|
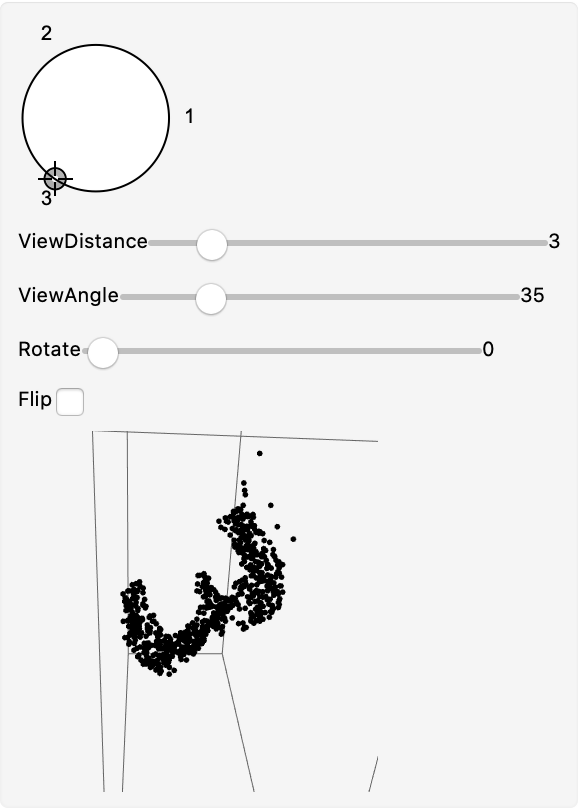
View the embedding with the resource function MultiPerspectiveEmbeddingViewer:
| In[5]:= |
![ResourceFunction["MultiPerspectiveEmbeddingViewer"][graphMPSE, "DisplayFunction" -> Function[Graphics3D[Point@graphMPSE["Embedding"], ##, AspectRatio -> 1, ImageSize -> Large]]]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/7dbc503283d6dd58.png)
|
| Out[5]= |
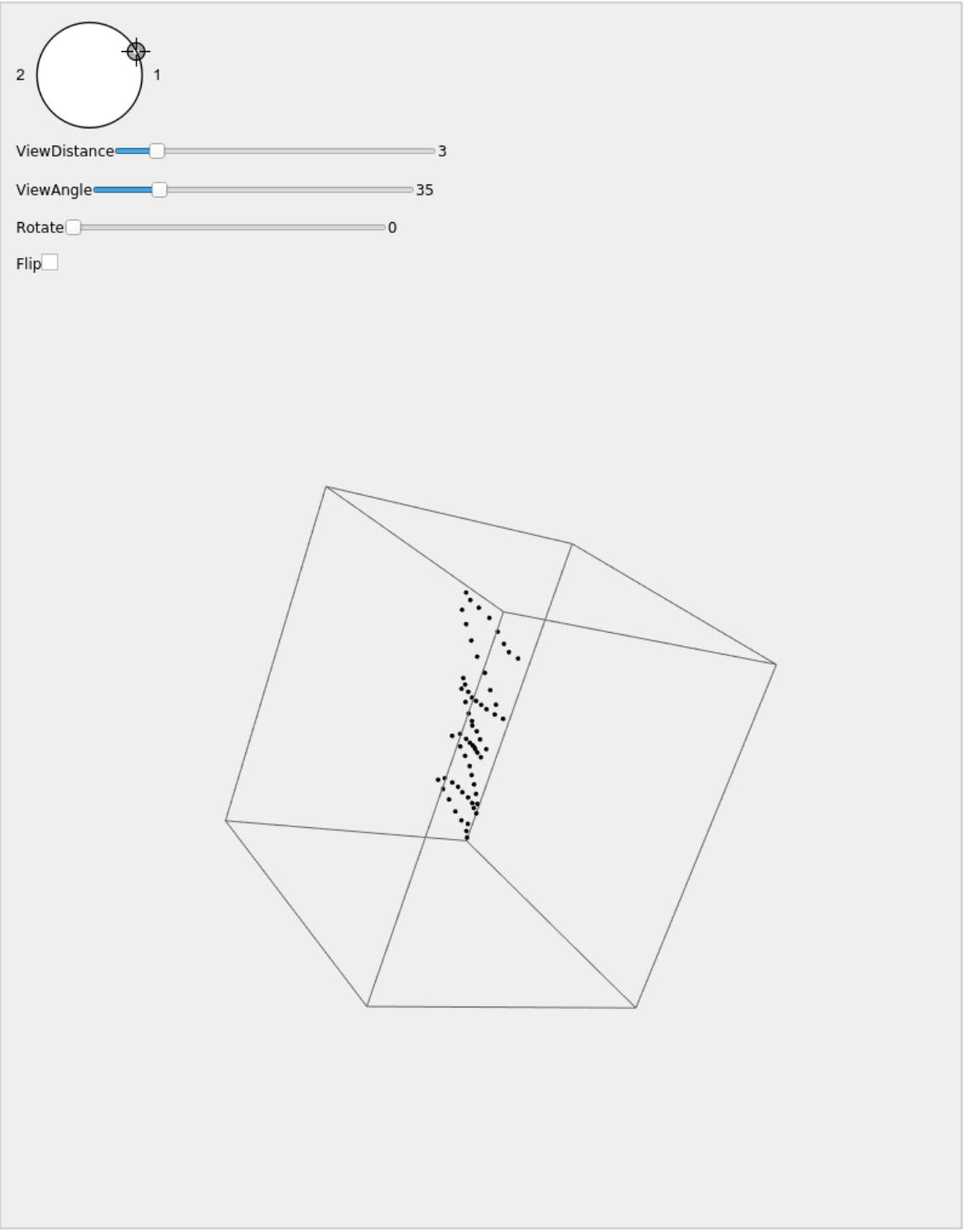
|
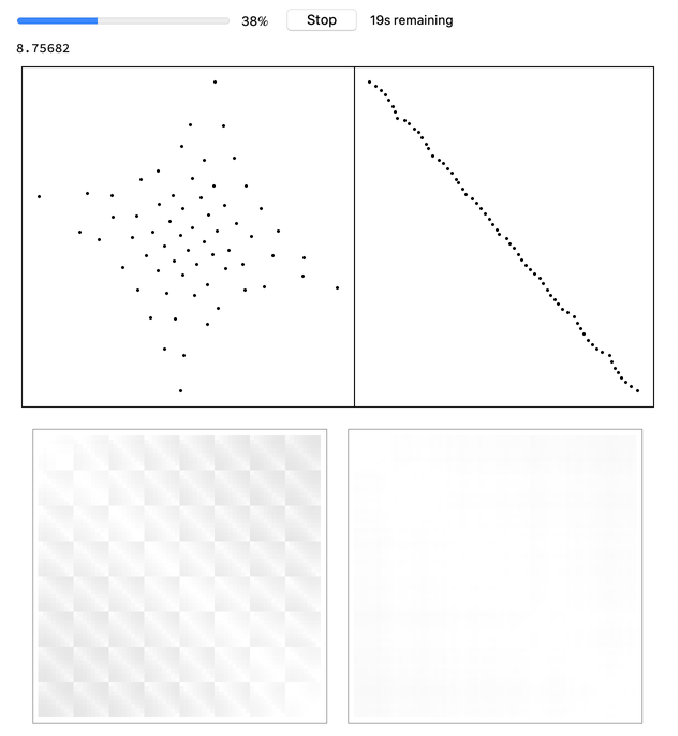
Here is the progress for training an embedding for points that look like digits 1, 2 and 3 in 2D from three distance matrices and how they form into their position:
| In[6]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4870c165-3fd6-4c47-b61e-50d7be9ad395"]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/159889764b759565.png)
|
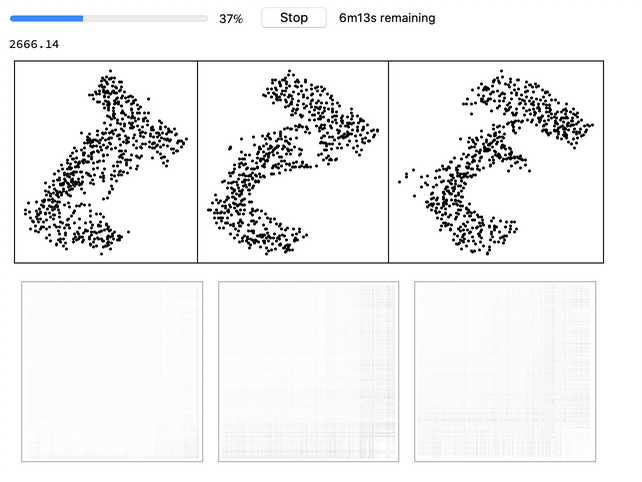
View the embedding:
| In[7]:= |
|
| Out[7]= |
|
Specify custom options for NetTrain, for example, MaxTrainingRounds:
| In[8]:= |
|
| Out[8]= |

|
Specify an initial embedding:
| In[9]:= |
![ResourceFunction[
"MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}, "NetTrainOptions" -> {MaxTrainingRounds -> 1}, "InitialEmbedding" -> Append[0] /@ GraphEmbedding[GridGraph[{4, 4}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/1d1b72b08d2ed456.png)
|
| Out[9]= |

|
Specify initial normal projection vectors using the "InitialProjection" option. The "Normals" key of the resulting association would contain new projection normal vectors after training:
| In[10]:= |
|
| Out[10]= |

|
Disable learning for normal vectors. The "Normals" value stays the same:
| In[11]:= |
![ResourceFunction[
"MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}, "NetTrainOptions" -> {MaxTrainingRounds -> 1}, "InitialProjection" -> {{1, 0, 0}, {0, 1, 0}}, "FixProjection" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/32333bb21a8b53a0.png)
|
| Out[11]= |

|
By default, distances are taken to be the distances between its graph embeddings:
| In[12]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9de89ea1-9427-41af-b85f-a0d9570d2caa"]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/62911599b3991ea0.png)
|

UseGraphEmbedding → False would use GraphDistanceMatrix instead:
| In[13]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9678d836-0077-4e6d-8e9a-08b1ef083799"]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/714308705ff57788.png)
|
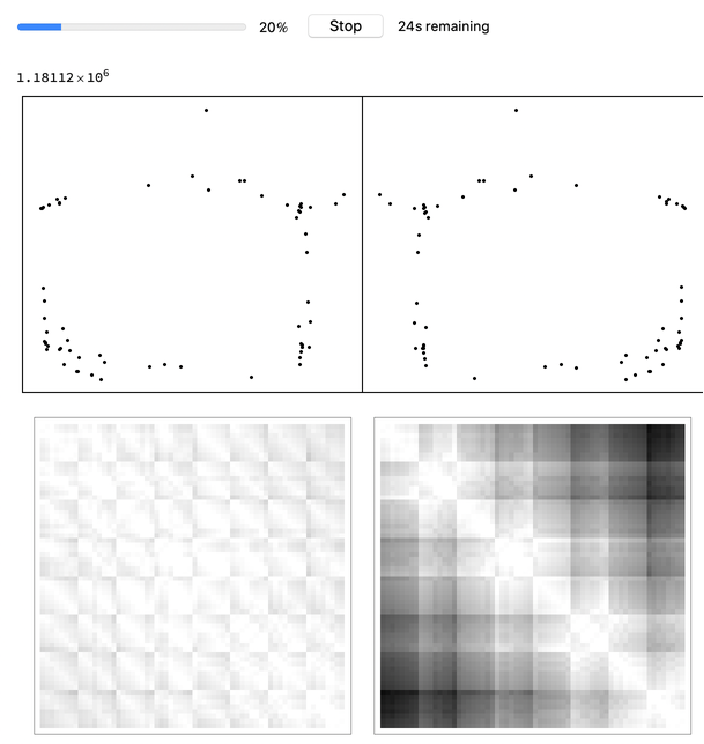
Without normalizing distances, training may diverge:
| In[14]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7e55aa1e-38dc-4fe9-beb2-48e33ecbcd21"]](https://www.wolframcloud.com/obj/resourcesystem/images/afc/afc96c72-1079-49ea-894e-dbd8d0fef894/6274110b320a3a9e.png)
|
This work is licensed under a Creative Commons Attribution 4.0 International License