Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a mini-max approximation of a function
ResourceFunction["MiniMaxApproximation"][expr,{x,{x0,x1},m,n}] finds the rational polynomial function of x, with numerator order m and denominator order n, that gives a mini-max approximation to expr on the interval x0 to x1. | |
ResourceFunction["MiniMaxApproximation"][expr,approx,{x,{x0,x1},m,n}] finds the mini-max approximation to expr, starting the iterative algorithm with approx. |
| "Bias" | 0 | bias in the automatic choice of interpolation points |
| "Brake" | {5,5} | braking to apply on the iterative algorithm |
| "Derivatives" | Automatic | function to use for derivatives |
| MaxIterations | 20 | maximum number of iterations to use |
| "PlotFlag" | False | whether to plot relative error |
| "PrintFlag" | False | whether to print status information |
| WorkingPrecision | MachinePrecision | precision to use in internal computations |
A list containing the points where the maximum error occurs and the desired interpolation, along with the value of the error:
| In[1]:= |
| Out[1]= |
The rational approximation:
| In[2]:= |
| Out[2]= |
The relative error in the approximation over the interval:
| In[3]:= |
| Out[3]= | 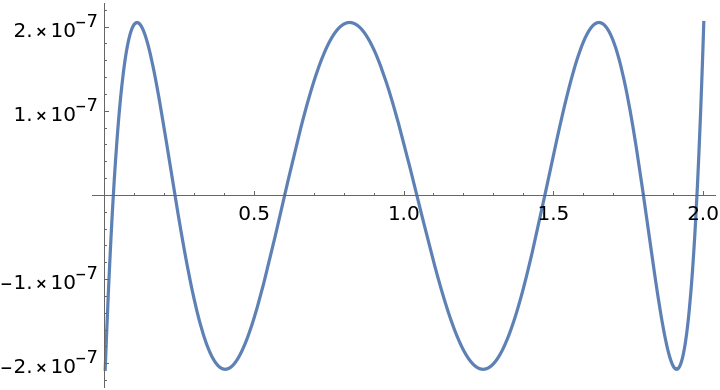 |
The convergence process does not finish within a small number of iterations without braking:
| In[4]:= |
| Out[4]= | 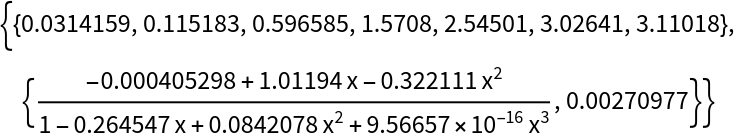 |
With the default brake, the conversion succeeds:
| In[5]:= |
| Out[5]= | 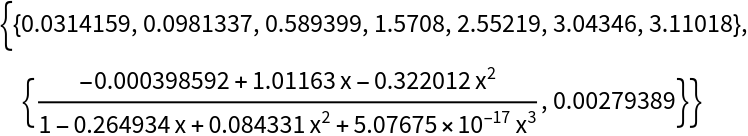 |
Supply a function that gives a list of derivatives of the function to be approximated, evaluated at numeric points:
| In[6]:= |
| In[7]:= |
| Out[7]= |
Because MiniMaxApproximation tries to minimize the maximum of the relative error, it is not possible to find a minimax approximation to a function that has a zero in the interval in question:
| In[8]:= |
| Out[8]= |
Divide out the zero and then multiply back into the rational function:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
The relative error:
| In[11]:= |
| Out[11]= | 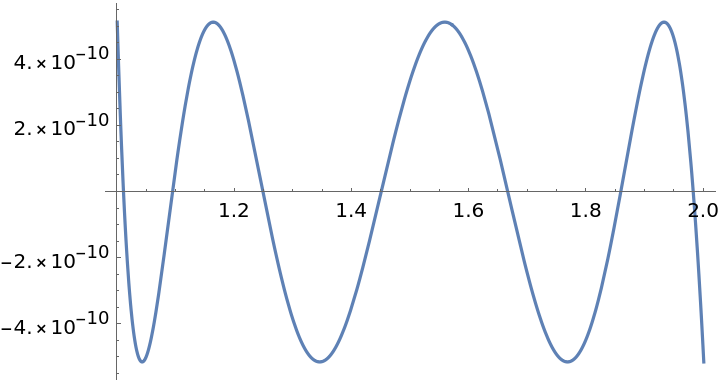 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License