Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a rational interpolation of a function
ResourceFunction["RationalInterpolation"][expr,{x,m,n},{x1,x2,…,xn+m+1}] gives the rational interpolant to expr with numerator order m and denominator order n, where x1,x2,… are the abscissas of the interpolation points. | |
ResourceFunction["RationalInterpolation"][expr,{x,m,n},{x,x0,x1}] gives the rational interpolant with the interpolation points chosen automatically on the interval x0 to x1. |
| WorkingPrecision | MachinePrecision | precision to use in internal computations | |
| "Bias" | 0 | bias in the automatic choice of interpolation points |
A rational interpolation of degree (2,4) to ex at seven equally spaced points between 0 and 2:
| In[1]:= |
| Out[1]= |
The error between the function and the approximation tends to get larger near the endpoints:
| In[2]:= |
| Out[2]= | 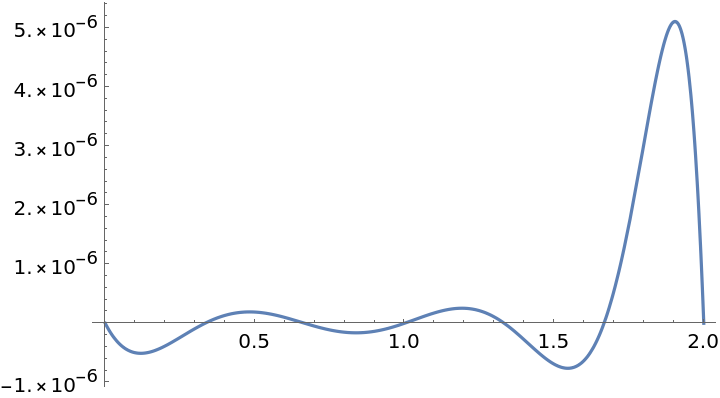 |
Automatically choosing the interpolation points results in a smaller maximum error:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= | 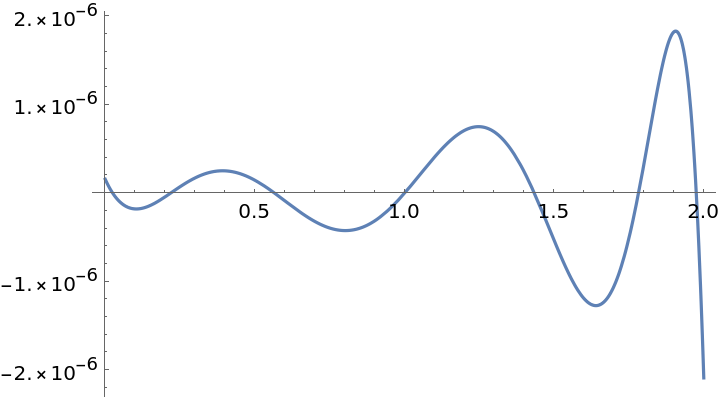 |
Bias the distribution of the points to the right to get smaller errors there and larger errors to the left:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= | 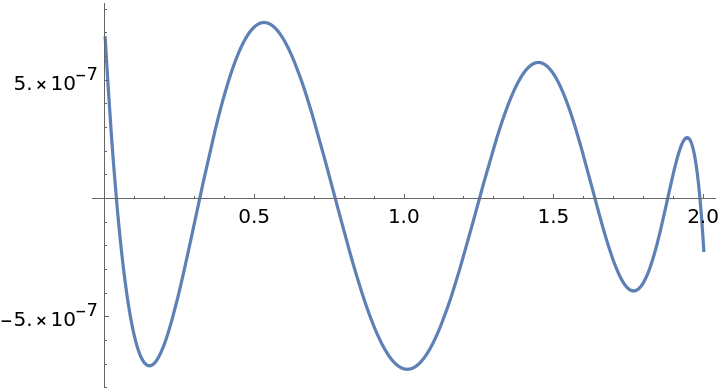 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License