Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MandelbrotSetRemap

Source Notebook

Apply functions to remap the Mandelbrot set

Contributed by: Mark Greenberg and Rohit Namjoshi

ResourceFunction["MandelbrotSetRemap"][cen, mag]

renders a smooth mapping of the Mandelbrot set centered on cen with a magnification of mag.

Details and Options

The center cen should be a complex number.
The magnification mag can be any positive number, though greater magnification requires a higher MaxIterations setting to see the details and therefore longer render time. If mag is omitted, a default value of 1.25 is used.
ResourceFunction["MandelbrotSetRemap"] accepts the following options:
ColorFunctionAutomaticcolor applied to each pixel's remapped value v where 0 ≤ v ≤ 1.
ColorFunctionScalingTrueif True,v will be scaled to 0 ≤ v ≤ 1.
ImageSize{260,200}size of the image.
"MappingFunction""Smooth"function that remaps the Mandelbrot Set.
MaxIterations16maximum number of iterations for a pixel. Higher values give more detail and longer render times.
"Parallel"Falsewhether ParallelMap should be used to speed up computation. Using "Parallel" with a preset will slow down the computation.
"Parameter1"-.7+.77ia complex parameter. See the "MappingFunction" table below
“Parameter2”1.33+77ia complex parameter. See the “MappingFunction” table below
“Parameter3”-.13-.77ia complex parameter. See the “MappingFunction” table below
“Parameter4”-1.9-.77ia complex parameter. See the “MappingFunction” table below
“Parameter5”2.a real parameter. See the “MappingFunction” table below
“Parameter6”1.a real parameter. See the “MappingFunction” table below
If "MappingFunction" is a custom function that outputs a list of values, ColorFunction should accept a list as its argument.
ImageSize→w is equivalent to ImageSize→{w,w}.
Render times can increase greatly for larger images or complicated functions.
The "MappingFunction" option has several presets:
"Beanstalks"based on the distance to the corners of the image
"Cobweb"based on the final value of IntegerPart[zre] + Round[zim] + "Parameter1"
"DandelionSeeds"based on the weighted distances between three points (located by "Parameter1", "Parameter2", and "Parameter3") with weights provided by "Parameter5" and "Parameter6"
“Decomposition”based on the final vector angle of z
"Filigree"based on the maximum absolute value of the vector angle of z
"Foliage"based on the maximum vector angle of z
"LineOrbitTrap"based on the minimum distance of z to a line passing through "Parameter2" and "Parameter3"
"ModTrailings"based on the modulus of z
"ParallelogramOrbitTrap"based on the distance to a quadrilateral (default is a parallelogram) with vertices at "Parameter1" through "Parameter4" and multipliers of "Parameter5" and "Parameter6"
"RibsAndTusks"based on the minimum and maximum distance to a quadrilateral with vertices on the image corners and multipliers of “Parameter5” and “Parameter6”
"Smooth"(default) gives a smooth gradient inside and outside
"ThreePointsOrbitTrap"based on the minimum distance of z to equlateral triangle vertices (default) or any triangle defined by the vertices at "Parameter1" through "Parameter3"
Each preset mapping function is compiled when it is first used, which can take several seconds to complete. Subsequent calls use the compiled version which is significantly faster.
The definition for a custom MappingFunction should accept ten arguments, customMapping[px, center, corner, maxIt,param1,param2,param3,param4,param5,param6]:
pxcomplex location of the pixel currently being remapped
centercomplex location of the image's center
cornercomplex location of the image's lower-left corner
maxItmaximum number of iterations
param1...param4complex numbers potentially provided by the user
param5,param6real numbers potentially provided by the user
center and corner are useful for mappings that scale or are aware of the image dimensions.

Examples

Basic Examples (2) 

Render a smooth mapping of the whole Mandelbrot set:

In[1]:=
ResourceFunction["MandelbrotSetRemap"][-.7]
Out[1]=

Zoom into part of the Mandelbrot set:

In[2]:=
ResourceFunction["MandelbrotSetRemap"][.385 - .27 I, 100, MaxIterations -> 48]
Out[2]=
In[3]:=
ResourceFunction["MandelbrotSetRemap"][-1.4, 36, MaxIterations -> 54]
Out[3]=

Options (9) 

ColorFunction (3) 

Use one of the presets, the default "BlueGold" or more vibrant color functions called "Vivid" and "Psychedelic":

In[4]:=
Table[ResourceFunction["MandelbrotSetRemap"][-.7, ColorFunction -> cf], {cf, {"BlueGold", "Vivid", "Psychedelic"}}]
Out[4]=

Assign a built-in color scheme to the mapping:

In[5]:=
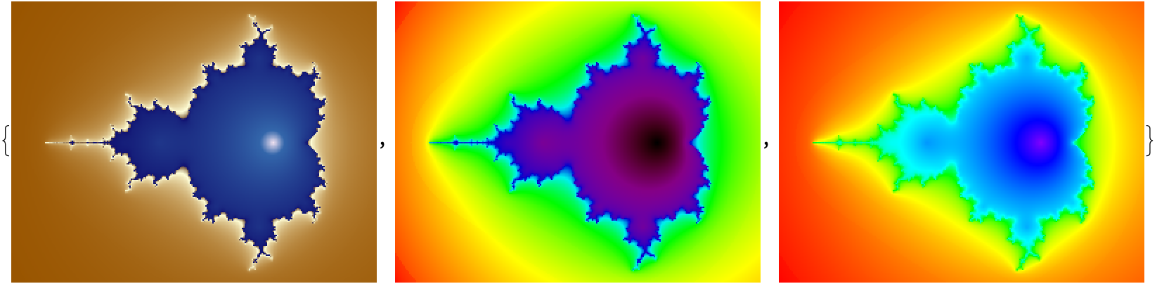
Table[ResourceFunction["MandelbrotSetRemap"][-.7, ColorFunction -> cf], {cf, {"Rainbow", "BoldColorFractalGradient", ColorData[{"TemperatureMap", "Reversed"}]}}]
Out[5]=

Use the value(s) returned by the MappingFunction as input to RGBColor, Hue, or any function that returns a color:

In[6]:=
Table[ResourceFunction["MandelbrotSetRemap"][-.7, ColorFunction -> cf], {cf, {RGBColor[.5, #, #] &, Hue[#, #, Sqrt[#]] &}}]
Out[6]=

ColorFunctionScaling (1) 

Set the ColorFunctionScaling option to False to use values outside 0 ≤ v ≤ 1 in custom color functions:

In[7]:=
Table[ResourceFunction["MandelbrotSetRemap"][-.7, ColorFunction -> (Hue[.75 - #, 1, Mod[#, 1] + .25] &), ColorFunctionScaling -> cfs], {cfs, {True, False}}]
Out[7]=

ImageSize (1) 

The ImageSize may be given as a single number for a square image or {w,h}:

In[8]:=
Table[ResourceFunction["MandelbrotSetRemap"][-.7, ImageSize -> sz], {sz, {260, {260, 100}}}]
Out[8]=

MappingFunction (2) 

Use one of twelve preset mapping functions:

In[9]:=
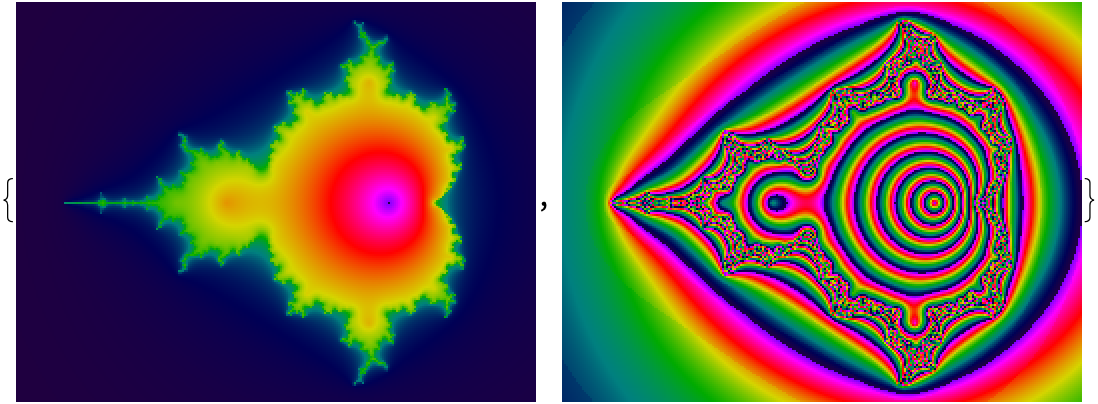
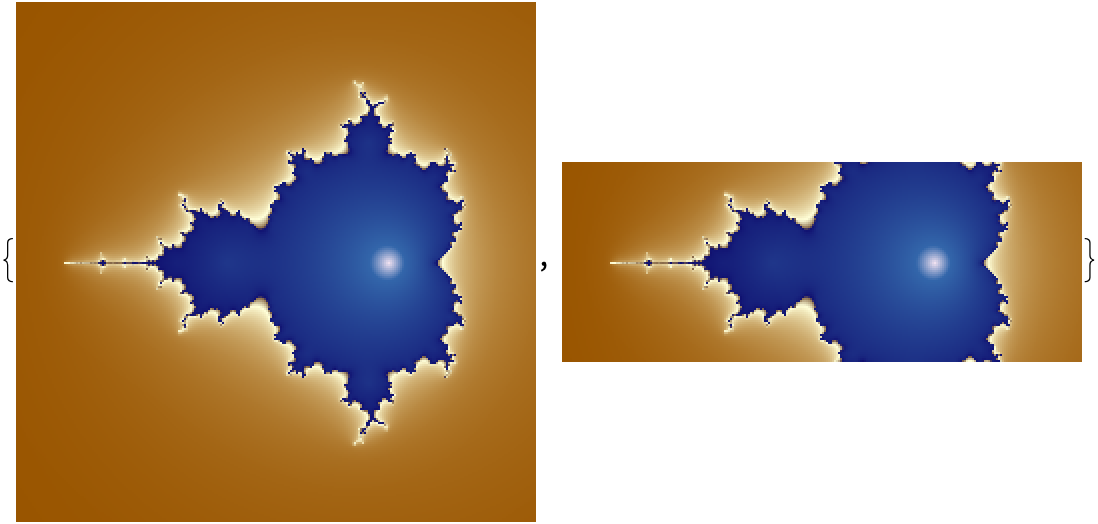
Table[Column[{mf, ResourceFunction["MandelbrotSetRemap"][-.7, "MappingFunction" -> mf]}, Alignment -> Center], {mf, {"Beanstalks", "Cobweb", "DandelionSeeds", "Decomposition", "Filigree", "Foliage", "LineOrbitTrap", "ModTrailings", "ParallelogramOrbitTrap", "RibsAndTusks", "Smooth", "ThreePointsOrbitTrap"}}]
Out[9]=

Explore artistic possibilities by zooming in:

In[10]:=
Table[Column[{mf, ResourceFunction["MandelbrotSetRemap"][-.049 - .84 I, 200, MaxIterations -> 30, "MappingFunction" -> mf]}, Alignment -> Center], {mf, {"Beanstalks", "Cobweb", "DandelionSeeds", "Decomposition", "Filigree", "Foliage", "LineOrbitTrap", "ModTrailings", "ParallelogramOrbitTrap", "RibsAndTusks", "Smooth", "ThreePointsOrbitTrap"}}]
Out[10]=

MaxIterations (1) 

Higher settings for MaxIterations give more details:

In[11]:=
Table[ResourceFunction["MandelbrotSetRemap"][-.7, ColorFunction -> "Vivid", MaxIterations -> mi], {mi, {8, 16, 48, 128}}]
Out[11]=

Parallel (1) 

Setting the Parallel option to True helps speed up complicated mapping functions:

In[12]:=
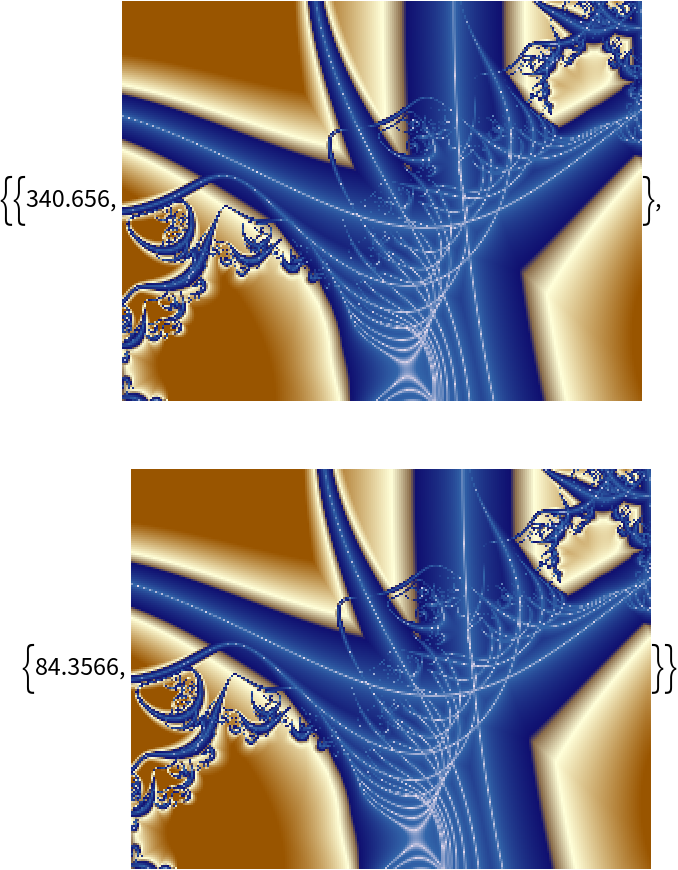
ellipseOrbitTrap = Function[{c, center, corner, maxIterations}, Module[{ trap, trapDist, list}, trap = Circle[{.8, 1}, {1.3, 2.7}]; trapDist = 1000000; list = NestWhileList[ (trapDist = Min[trapDist, RegionDistance[trap, ReIm[#]]]; #^2 + c) &, 0, Abs[#] <= 6 &, 1, maxIterations]; -Sqrt[trapDist] ]]; Table[AbsoluteTiming[ ResourceFunction["MandelbrotSetRemap"][-0.7 + .46 I, 2.8, "Parallel" -> p, "MappingFunction" -> ellipseOrbitTrap]], {p, {False, True}}]
Out[2]=

Applications (1) 

Make a cool image:

In[13]:=
ResourceFunction["MandelbrotSetRemap"][-.805 - .176 I, 170, MaxIterations -> 64, "MappingFunction" -> "ThreePointsOrbitTrap", ColorFunction -> ColorData["SunsetColors"], Parameter1 -> .2 - .5 I, ImageSize -> {600, 400}]
Out[13]=

Neat Examples (2) 

Combining images made with MandelbrotSetRemap can produce some spectacular results:

In[14]:=
img1 = ResourceFunction["MandelbrotSetRemap"][.08 + 1.009 I, 10, MaxIterations -> 32, "MappingFunction" -> "ModTrailings", ColorFunction -> "SunsetColors", ImageSize -> {600, 400}]; img2 = ResourceFunction["MandelbrotSetRemap"][.08 + 1.009 I, 10, "MappingFunction" -> "Decomposition", ColorFunction -> "FuchsiaTones", ImageSize -> {600, 400}]; ImageAdjust[ImageMultiply[{img1, img2}]]
Out[16]=

Here is the same part of the Mandelbrot set rendered with MandelbrotSetPlot and MandelbrotSetRemap using the same ColorFunction:

In[17]:=
Column[{ MandelbrotSetPlot[{.3535 - .0666 I, .361 - .062 I}, MaxIterations -> 42, ImageSize -> {600, 400}, ColorFunction -> "SunsetColors"], ResourceFunction["MandelbrotSetRemap"][.357 - .0644 I, 550, MaxIterations -> 42, ImageSize -> {600, 400}, ColorFunction -> "SunsetColors"], ResourceFunction["MandelbrotSetRemap"][.357 - .0644 I, 550, MaxIterations -> 42, ImageSize -> {600, 400}, "MappingFunction" -> "ParallelogramOrbitTrap", ColorFunction -> "SunsetColors"] }]
Out[17]=

Publisher

Mark Greenberg

Version History

  • 1.1.0 – 10 February 2023
  • 1.0.0 – 02 November 2021

License Information