Function Repository Resource:

LommelR

Source Notebook

Evaluate the Lommel polynomial

Contributed by: Jan Mangaldan

ResourceFunction["LommelR"][m,n,z]

gives the Lommel polynomial .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.

appears in the recursion relation

for Bessel functions.

Lommel polynomials are strictly rational functions and not polynomials. They were originally studied by Eugen von Lommel.

For certain special arguments, ResourceFunction["LommelR"] automatically evaluates to exact values.

ResourceFunction["LommelR"] can be evaluated to arbitrary numerical precision.

ResourceFunction["LommelR"] automatically threads over lists.

Examples

Basic Examples (3)

Evaluate numerically:

In[1]:=

Out[1]=

Evaluate Lommel polynomials for various degrees:

In[2]:=

Out[2]=

Plot R_4,2/3(x) over a subset of the reals:

In[3]:=

Out[3]=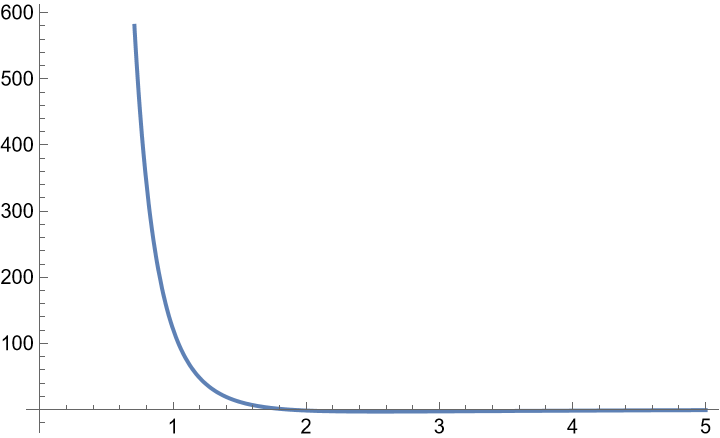

Scope (3)

Evaluate for complex arguments:

In[4]:=

Out[4]=

Evaluate to high precision:

In[5]:=

Out[5]=

The precision of the output tracks the precision of the input:

In[6]:=

Out[6]=

LommelR threads elementwise over lists:

In[7]:=

Out[7]=

Applications (2)

Use the Lommel polynomial to express in terms of and :

In[8]:=

With[{n = 5}, BesselJ[n, z] == ResourceFunction["LommelR"][n - 1, 1, z] BesselJ[1, z] - ResourceFunction["LommelR"][n - 2, 2, z] BesselJ[0, z]] // FullSimplify

Out[8]=

A similar relation holds for :

In[9]:=

With[{n = 5}, BesselY[n, z] == ResourceFunction["LommelR"][n - 1, 1, z] BesselY[1, z] - ResourceFunction["LommelR"][n - 2, 2, z] BesselY[0, z]] // FullSimplify

Out[9]=

Properties and Relations (6)

A determinantal representation for LommelR:

In[10]:=

$With[{m = 5, n = 3}, ResourceFunction["LommelR"][m, n, x] == Det[SparseArray[{{k_, k_} :> 2 (n + m - k)/x, Band[{2, 1}] -> 1, Band[{1, 2}] -> 1}, {m, m}]] // FullSimplify]$

Out[10]=

Represent LommelR in terms of BesselJ:

In[11]:=

$With[{m = 3, n = 1/2}, ResourceFunction["LommelR"][m, n, x] == x/(2 n Sinc[ n \[Pi]]) (BesselJ[n + m, x] BesselJ[1 - n, x] + (-1)^ m BesselJ[-n - m, x] BesselJ[n - 1, x]) // FullSimplify]$

Out[11]=

Verify Crelier's formula:

In[12]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/65981d81-be05-4d3f-9553-8b3dd9d535da"]

Out[12]=

Verify recurrence relations satisfied by LommelR:

In[13]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/803fac00-0bec-48c2-93d0-5beb221117bd"]

Out[13]=

In[14]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1a335570-b66e-4a85-b081-2e3e8bfd8283"]

Out[14]=

Verify the differential equation satisfied by LommelR:

In[15]:=

$With[{m = 5, n = 3}, x^4 y''''[x] + 2 x^3 y'''[x] + x^2 (-1 - 2 m^2 - 4 m n - 4 n (n - 1) + 4 x^2) y''[x] + x (8 x^2 + 2 m^2 + (1 - 2 n)^2 + 4 m n) y'[x] + m (m + 2) (2 n + m - 2) (2 n + m) y[x] == 0 /. y -> Function[x, ResourceFunction["LommelR"][m, n, x]] // FullSimplify]$