Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
The logit function from probability
ResourceFunction["Logit"][p] computes the logit of p. |
Compute the logit of an exact number:
| In[1]:= |
| Out[1]= |
Plot the logit function on the real line:
| In[2]:= |
| Out[2]= | 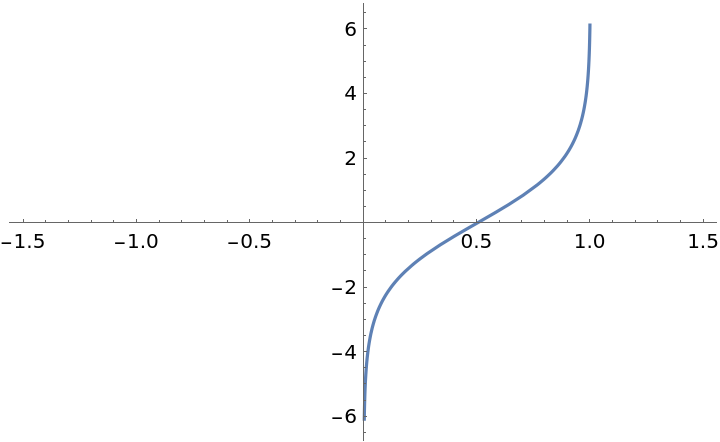 |
Compute the logit of an approximate number:
| In[3]:= |
| Out[3]= |
Logit[x] has a zero at x=1/2:
| In[4]:= |
| Out[4]= |
Apply Logit to symbolic input:
| In[5]:= |
| Out[5]= |
Logit automatically threads over lists:
| In[6]:= |
| Out[6]= |
Applying Logit to a real number x outside the range 0<x<1 gives a complex result:
| In[7]:= |
| Out[7]= |
Logit[x] evaluates to -∞ for x=0:
| In[8]:= |
| Out[8]= |
Logit[x] evaluates to ∞ for x=1:
| In[9]:= |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License