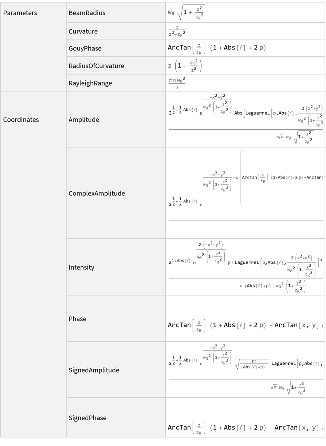
Details
Laguerre-Gaussian beams form a class of optical beams that generalize the Gaussian beam, exhibit cylindrical symmetry and have helical wavefronts. These beams have interesting properties such as quantized orbital angular momentum and applications e.g. in transmission of classical and quantum information. These beams constitute an orthonormal basis of the vector space of all possible beam profiles.
ResourceFunction["LaguerreGaussianBeam"] represents a Laguerre-Gaussian field that propagates along the vertical z-axis and that is parametrized by its beam waist w0, Rayleigh range zR, azimuthal mode number l and radial mode number p. The azimuthal mode number is an integer that can take on also negative values, whereas the radial mode number is a non-negative integer. Laguerre-Gaussian modes represent optical vortices, where the topological charge of the vortex is equal to the corresponding azimuthal mode number. The use of letters l and p for the two mode numbers is a standard convention.
Properties can be accessed by calling
ResourceFunction["LaguerreGaussianBeam"]["Properties"]. All available profiles and computed parameters are listed in
ResourceFunction["LaguerreGaussianBeam"]["Profiles"] and
ResourceFunction["LaguerreGaussianBeam"]["Parameters"], respectively. The formatted summary of all properties can be retrieved by
ResourceFunction["LaguerreGaussianBeam"]["Summary"].
Available "Profiles" include:
| "Amplitude" | non-negative amplitude of electromagnetic beam |
| "SignedAmplitude" | real amplitude that is negative iff Laguerre polynomials are negative |
| "ComplexAmplitude" | complex amplitude that includes both "Amplitude" and "Phase" |
| "Intensity" | square of (real) amplitude |
| "Phase" | phase of electromagnetic beam |
| "SignedPhase" | phase that complements "SignedAmplitude" |
Available "Parameters" include:
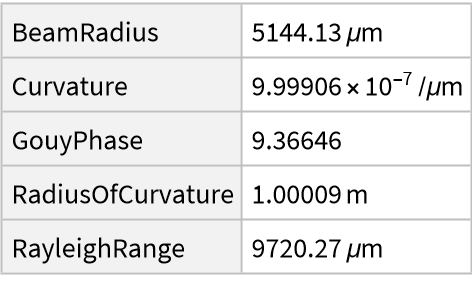
| "BeamRadius" | beam radius at given longitudinal position |
| "ComplexBeamParameter" | complex beam parameter |
| "Curvature" | beam curvature |
| "GouyPhase" | Gouy phase |
| "RadiusOfCurvature" | radius of curvature |
| "RayleighRange" | Rayleigh range |
The formula for a given computed parameter "par" is obtained by calling ResourceFunction["LaguerreGaussianBeam"][par]. For instance, the explicit formula for the Gouy phase is retrieved by calling ResourceFunction["LaguerreGaussianBeam"]["GouyPhase"].
Summary of all properties is returned by
ResourceFunction["LaguerreGaussianBeam"]["Summary"] in the form of
Dataset.
Not all beam parameters are independent of each other. The canonical set of independent parameters is the beam waist
w0, Rayleigh range
zR, azimuthal mode number
l and polar mode number
p, out of which all other properties can be calculated. The relation between
w0 and
zR reads
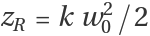
, where
k=2πn/λ is the beam's wavenumber and where further
n is the refractive index of the propagation medium and
λ is the beam's wavelength. Instead of
w0 and
zR one could thus choose any complete set of these characteristics to specify the beam. For that reason, there are several ways of specifying a Laguerre-Gaussian beam:
| {w0,zR,l,p} | specific beam waist, Rayleigh range, and the two mode numbers |
| "Normalized" | equivalent to w0=1,zR=1,l=1, and p=0 |
| <|k1→v1,k2→v2,…|> | Association with a set of independent parameters given as key-value pairs |
When the parameters are specified as an
Association, the following named keys are supported:
| "BeamWaist" | beam waist |
| "RayleighRange" | Rayleigh range |
| "Wavenumber" | wavenumber k=2πn/λ |
| "Wavelength" | wavelength λ |
| "RefractiveIndex" | refractive index n |
| "AzimuthalMode" | azimuthal mode number l (also referred to as topological charge) |
| "RadialMode" | radial mode number p |
There are also short keys supported for convenience:
| "w0" | beam waist |
| "zR" | Rayleigh range |
| "k" | wavenumber k=2πn/λ |
| "λ" | wavelength λ |
| "n" | refractive index n |
| "l" | azimuthal mode number l |
| "p" | radial mode number p |
Full and shortened keys can be used together in a single
Association, but a given parameter can be specified only once.
There are two possibilities for an independent set of parameters: 1) exactly two of w0, zR, and k are given together with both ℓ and p. 2) exactly one of w0 and zR together with all λ, n, ℓ, and p are given.
The input parameters can be specified in the following formats:
| v | symbolic variable |
| 0.325 | numeric value |
| Quantity[v,unit] | symbolic or numeric value with unit |
| QuantityVariable[v,unit] | named physical quantity with unit |
Two coordinate systems are supported which can be specified with a second argument:
| "Cartesian" | Cartesian coordinates {x,y,z} (default) |
| "Cylindrical" | cylindrical coordinates {r,ϕ,z} |
The Laguerre-Gaussian beam formula depends explicitly on several computed parameters such as beam radius and radius of curvature. These are by default automatically expanded into their functional representation. One can suppress this expansion by setting the third argument to
False. This turns the parameters into
QuantityVariable objects and the beam formula is thus returned in its higher-level form. Such a form might be beneficial when rendering the formula in some text or for reference purposes.
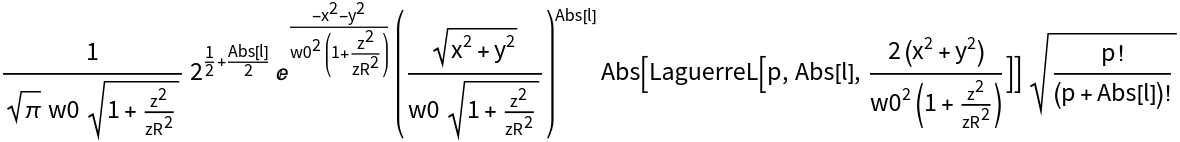
![xint = Table[
ResourceFunction[
"LaguerreGaussianBeam"][{"Intensity", <|"BeamWaist" -> 0.3, "RayleighRange" -> 1.0, "AzimuthalMode" -> 1, "RadialMode" -> 1|>}][x, 0, 0], {x, -1, 1, 0.01}];
Short[xint]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/3b8aa8f011fce8dd.png)

![ResourceFunction[
"LaguerreGaussianBeam"][{"Summary", <|
"w0" -> Quantity[50, "Micrometers"], "n" -> 1., "\[Lambda]" -> Quantity[808, "Nanometers"], "l" -> -1, "p" -> 2|>,
Quantity[1, "Meters"]}]["Parameters"]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/61232398f2323e94.png)
![DensityPlot[
Mod[ResourceFunction[
"LaguerreGaussianBeam"][{"Phase", {1, 1, 5, 1}}][x, y, 0], 2 \[Pi]], {x, -2, 2}, {y, -2, 2}, Exclusions -> {x < 0}, PlotPoints -> 80]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/50e358fb29a7b35d.png)
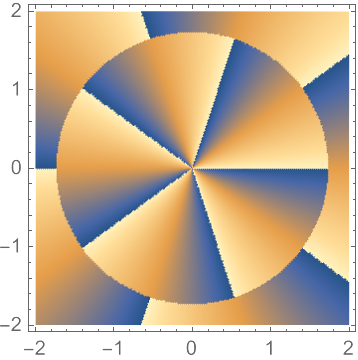

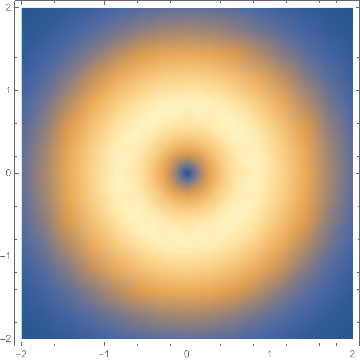
![zpos = 0.5;
beam = ResourceFunction[
"LaguerreGaussianBeam"][{"Amplitude", {1, 1, 1, 0}, zpos}];
DensityPlot[beam[x, y], {x, -2, 2}, {y, -2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/2b0437ada0fd1fed.png)
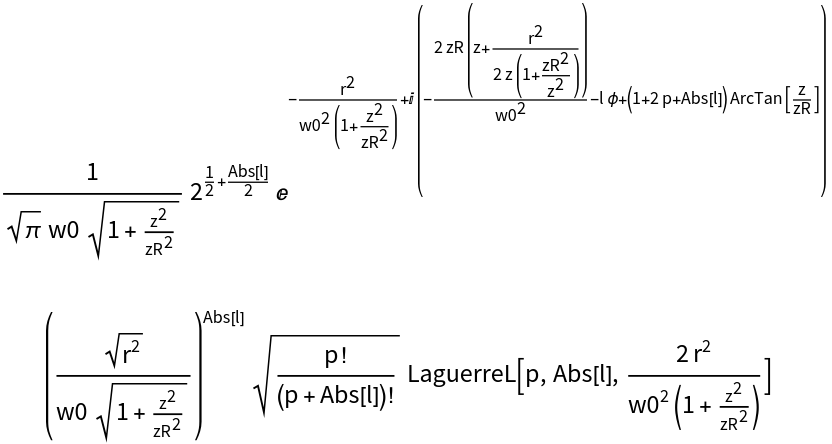
![ResourceFunction["LaguerreGaussianBeam"][spec, "Cartesian"][x, y, z] ==
ResourceFunction["LaguerreGaussianBeam"][spec, "Cylindrical"][##,
z] & @@ ToPolarCoordinates[{x, y}] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/6152c92c9db38d68.png)
![ResourceFunction["LaguerreGaussianBeam"][spec, "Cylindrical"][
r, \[Phi], z] == ResourceFunction["LaguerreGaussianBeam"][spec, "Cartesian"][##, z] & @@ FromPolarCoordinates[{r, \[Phi]}] // Simplify[# /. ArcTan[r Cos[\[Phi]], r Sin[\[Phi]]] -> \[Phi]] &](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/72a7104e1f0c0753.png)
![{
ResourceFunction["LaguerreGaussianBeam"]["Curvature"],
ResourceFunction["LaguerreGaussianBeam"][{"Curvature", zR}],
ResourceFunction["LaguerreGaussianBeam"][{"Curvature", 0.5}][1.3],
ResourceFunction["LaguerreGaussianBeam"][{"Curvature", 0.5, 1.3}],
ResourceFunction[
"LaguerreGaussianBeam"][{"Curvature", <|"RayleighRange" -> 0.5|>, 1.3}]
}](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/47f09b6f09a7c84f.png)
![{
ResourceFunction[
"LaguerreGaussianBeam"][{"Curvature", QuantityVariable["zR", "Distance"], QuantityVariable["z", "Distance"]}],
ResourceFunction[
"LaguerreGaussianBeam"][{"Curvature", Quantity[zR, "Millimeters"], Quantity[z, "Millimeters"]}],
ResourceFunction[
"LaguerreGaussianBeam"][{"Curvature", Quantity[1, "Millimeters"], Quantity[5.0, "Millimeters"]}]
}](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/5fecd6b235507d17.png)
![{
ResourceFunction["LaguerreGaussianBeam"][{"BeamRadius", {w0, zR}, z}],
ResourceFunction["LaguerreGaussianBeam"][{"GouyPhase", {zR, l, p}, z}]
}](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/149176a2bf10c033.png)
![ResourceFunction[
"LaguerreGaussianBeam"][{"BeamRadius", {w0, zR}, z}] /. zR -> ResourceFunction[
"LaguerreGaussianBeam"][{"RayleighRange", {w0, \[Lambda], n}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/481ed4d633d7409d.png)
![lmode = 5;
zpos = 0.5;
lgPlus = ResourceFunction[
"LaguerreGaussianBeam"][{"ComplexAmplitude", {1, 1, lmode, 0}}][x,
y, zpos];
lgMinus = ResourceFunction[
"LaguerreGaussianBeam"][{"ComplexAmplitude", {1, 1, -lmode, 0}}][
x, y, zpos];
superposition = Simplify[lgPlus + lgMinus]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/0cb72bff3d1980fe.png)
![intensity = ComplexExpand[superposition\[Conjugate] superposition];
DensityPlot[intensity, {x, -5, 5}, {y, -5, 5}, PlotRange -> All, Exclusions -> {x < 0}, PlotPoints -> 50]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/00d7d92cf8f957c2.png)
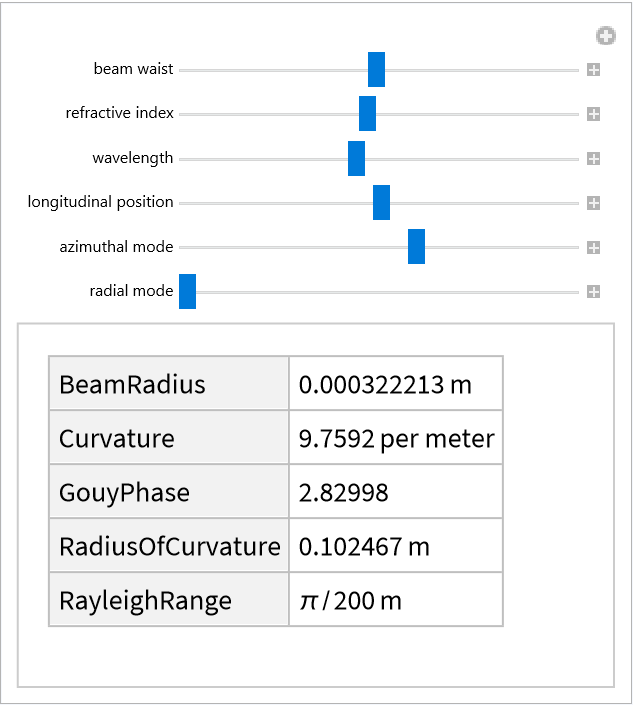
![Manipulate[
UnitConvert@Quiet@ResourceFunction["LaguerreGaussianBeam"][{"Summary",
Association["w0" -> Quantity[w0val, "Micrometers"], "n" -> nval,
"\[Lambda]" -> Quantity[\[Lambda]val, "Nanometers"], "l" -> lval, "p" -> pval]
, Quantity[zval, "Meters"]}]["Parameters"],
{{w0val, 50, "beam waist"}, 1, 100}, {{nval, 1, "refractive index"}, 0.1, 2},
{{\[Lambda]val, 500, "wavelength"}, 100, 1000}, {{zval, 0.1, "longitudinal position"}, -5, 5},
{{lval, 1, "azimuthal mode"}, -5, 5, 1}, {{pval, 0, "radial mode"}, 0, 5, 1}
]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/01b7307b083eebcb.png)
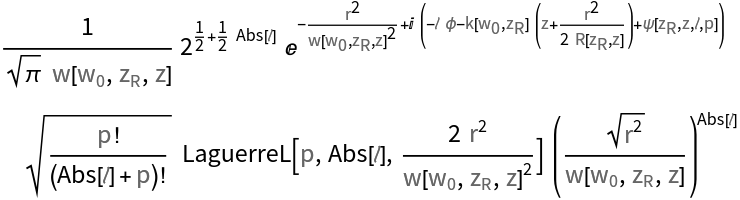
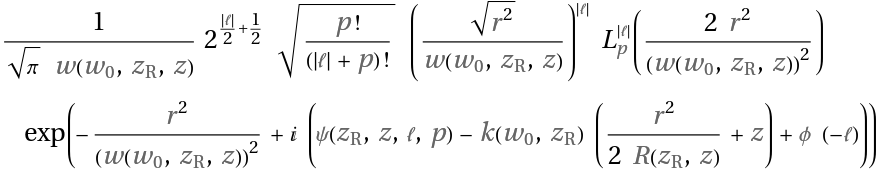

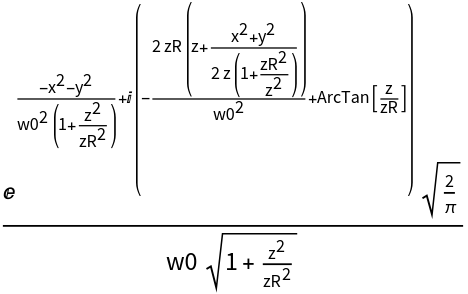
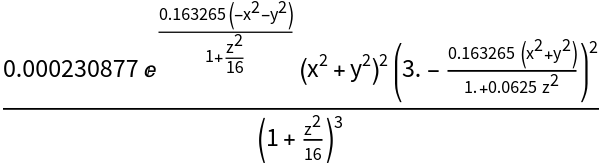
![With[{i = ResourceFunction[
"LaguerreGaussianBeam"][{"Intensity", {w0, zR, l, p}}][x, y, z], a = ResourceFunction[
"LaguerreGaussianBeam"][{"Amplitude", {w0, zR, l, p}}][x, y, z]},
Simplify[i == a^2, {
Element[
Blank[LaguerreL], Reals]}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/755a45fdc4cd105f.png)
![With[{a = ResourceFunction[
"LaguerreGaussianBeam"][{"Amplitude", {w0, zR, l, p}}][x, y, z], sa = ResourceFunction[
"LaguerreGaussianBeam"][{"SignedAmplitude", {w0, zR, l, p}}][x, y, z]},
Simplify[a == Abs[sa], {w0 > 0, zR > 0,
Element[{x, y, z}, Reals],
Element[{l, p}, NonNegativeIntegers]}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/592a9eb9db6c2d85.png)
![With[{p = ResourceFunction[
"LaguerreGaussianBeam"][{"Phase", {w0, zR, l, p}}][x, y, z], sp = ResourceFunction[
"LaguerreGaussianBeam"][{"SignedPhase", {w0, zR, l, p}}][x, y, z]},
Simplify[p - sp]
]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/17049737ea4be229.png)
![With[{ca = ResourceFunction[
"LaguerreGaussianBeam"][{"ComplexAmplitude", {w0, zR, l, p}}][x, y, z], a = ResourceFunction[
"LaguerreGaussianBeam"][{"Amplitude", {w0, zR, l, p}}][x, y, z], ph = ResourceFunction[
"LaguerreGaussianBeam"][{"Phase", {w0, zR, l, p}}][x, y, z]},
Simplify@PiecewiseExpand[ca == a Exp[I ph]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/65e620d8c5978baa.png)
![With[{ca = ResourceFunction[
"LaguerreGaussianBeam"][{"ComplexAmplitude", {w0, zR, l, p}}][x, y, z], a = ResourceFunction[
"LaguerreGaussianBeam"][{"SignedAmplitude", {w0, zR, l, p}}][x, y, z], ph = ResourceFunction[
"LaguerreGaussianBeam"][{"SignedPhase", {w0, zR, l, p}}][x, y, z]},
Simplify[ca == a Exp[I ph]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/4f61b473c5629a4a.png)
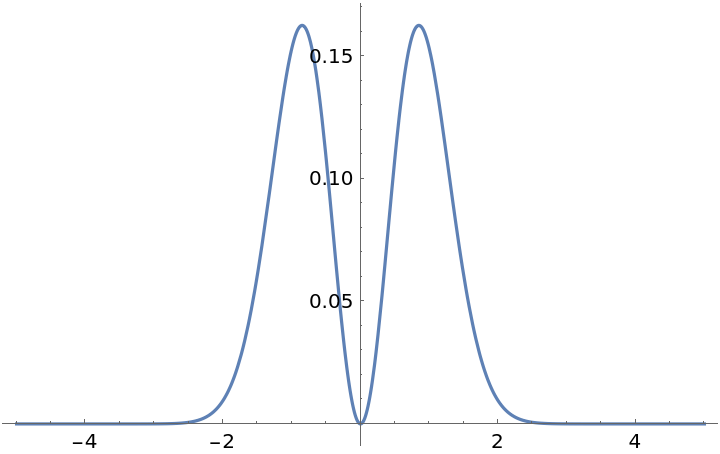
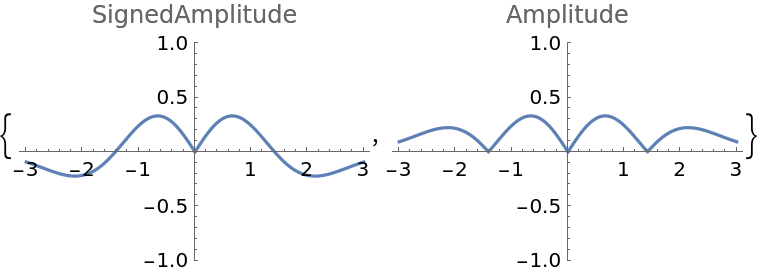
![Plot[ResourceFunction["LaguerreGaussianBeam"][{#, {1, 1, -1, 1}}][0, y, 1], {y, -3, 3}, PlotLabel -> #, PlotRange -> {All, {-1, 1}}] & /@ {"SignedAmplitude", "Amplitude"}](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/5652d1ccc8621957.png)
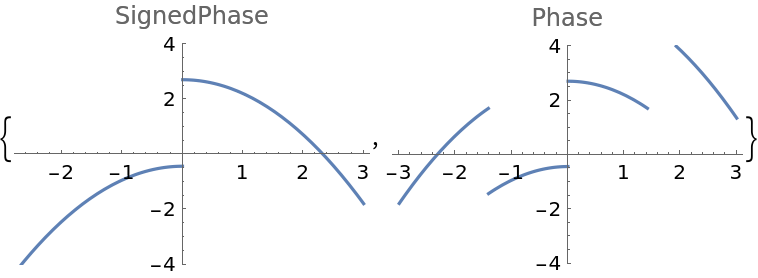
![Plot[ResourceFunction["LaguerreGaussianBeam"][{#, {1, 1, -1, 1}}][0, y, 1], {y, -3, 3}, PlotLabel -> #, PlotRange -> {All, {-4, 4}}] & /@ {"SignedPhase", "Phase"}](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/1ea78d900e17d745.png)
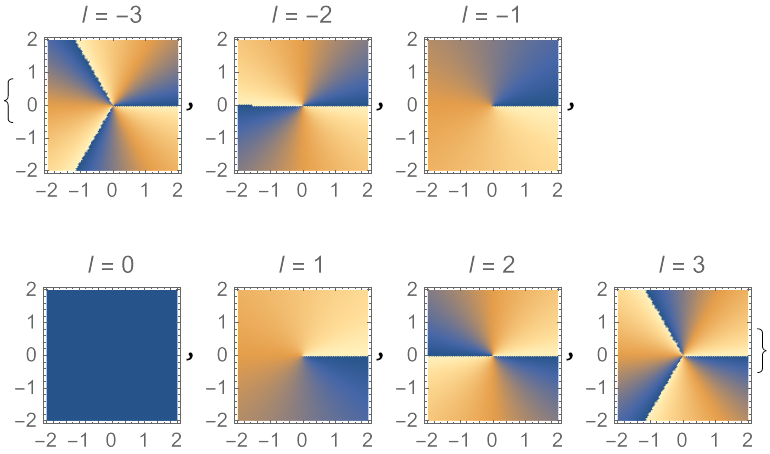
![Table[DensityPlot[
Mod[ResourceFunction[
"LaguerreGaussianBeam"][{"Phase", {1, 1, tc, 0}}][x, y, 0], 2 \[Pi]], {x, -2, 2}, {y, -2, 2}, Exclusions -> {x < 0}, PlotPoints -> 30, PlotLabel -> TemplateApply["\!\(\*
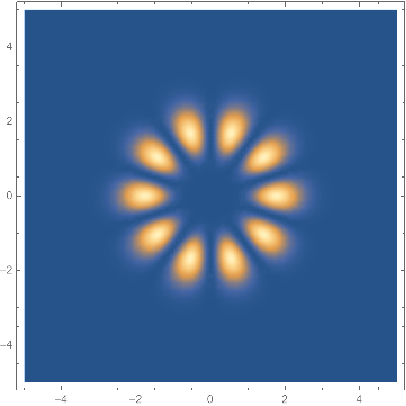
StyleBox[\"l\",\nFontSlant->\"Italic\"]\) = ``", tc], ImageSize -> Tiny], {tc, -3, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/0e5bf83c314cf9c0.png)
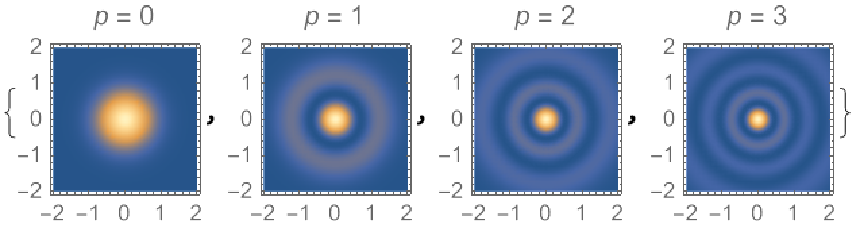
![Table[DensityPlot[
Mod[ResourceFunction[
"LaguerreGaussianBeam"][{"Intensity", {1, 1, 0, p}}][x, y, 0], 2 \[Pi]], {x, -2, 2}, {y, -2, 2}, PlotPoints -> 30, PlotLabel -> TemplateApply["\!\(\*
StyleBox[\"p\",\nFontSlant->\"Italic\"]\) = ``", p], PlotRange -> All,
ImageSize -> Tiny], {p, 0, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/535af37b9ccddf43.png)
![tab = Table[
DensityPlot[
Mod[ResourceFunction[
"LaguerreGaussianBeam"][{"Intensity", {1, 1, tc, rm}}][x, y, 0], 2 \[Pi]], {x, -2, 2}, {y, -2, 2}, Exclusions -> {x < 0}, PlotPoints -> 20, ImageSize -> Tiny, FrameTicks -> False, PlotRange -> All], {rm, 0, 2}, {tc, 0, 2}];
Grid[Transpose@Join[{{"", "\!\(\*
StyleBox[\"p\",\nFontSlant->\"Italic\"]\)=0", "\!\(\*
StyleBox[\"p\",\nFontSlant->\"Italic\"]\)=1", "\!\(\*
StyleBox[\"p\",\nFontSlant->\"Italic\"]\)=2"}}, Transpose[Join[{{"\!\(\*
StyleBox[\"l\",\nFontSlant->\"Italic\"]\)=0", "\!\(\*
StyleBox[\"l\",\nFontSlant->\"Italic\"]\)=1", "\!\(\*
StyleBox[\"l\",\nFontSlant->\"Italic\"]\)=2"}}, tab]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/24589638b7108618.png)
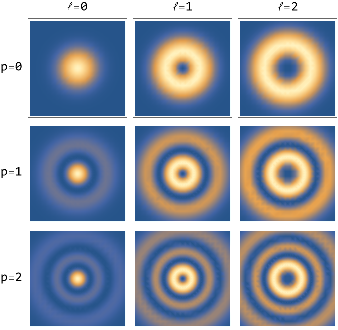
![intensity = ResourceFunction[
"LaguerreGaussianBeam"][{"Intensity", {1, 2, 1, 0}}];
DensityPlot3D[
intensity[x, y, z], {x, -15, 15}, {y, -15, 15}, {z, -15, 15}, PlotLabel -> "Absolute intensity", PlotPoints -> 70, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/28e0bb3b2e7c5fc1.png)
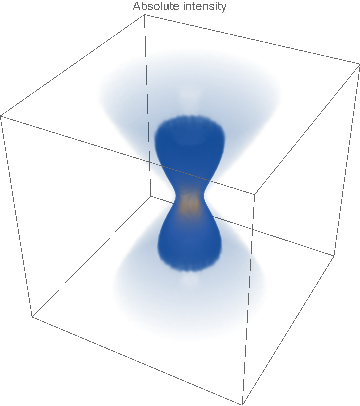
![DensityPlot3D[
intensity[x, y, z]/
intensity[Sqrt[4 + z^2]/(2 Sqrt[2]), 0, z], {x, -15, 15}, {y, -15, 15}, {z, -15, 15}, PlotLabel -> "Relative intensity", Axes -> False,
OpacityFunction -> "Image3D"]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/65e1856206663689.png)
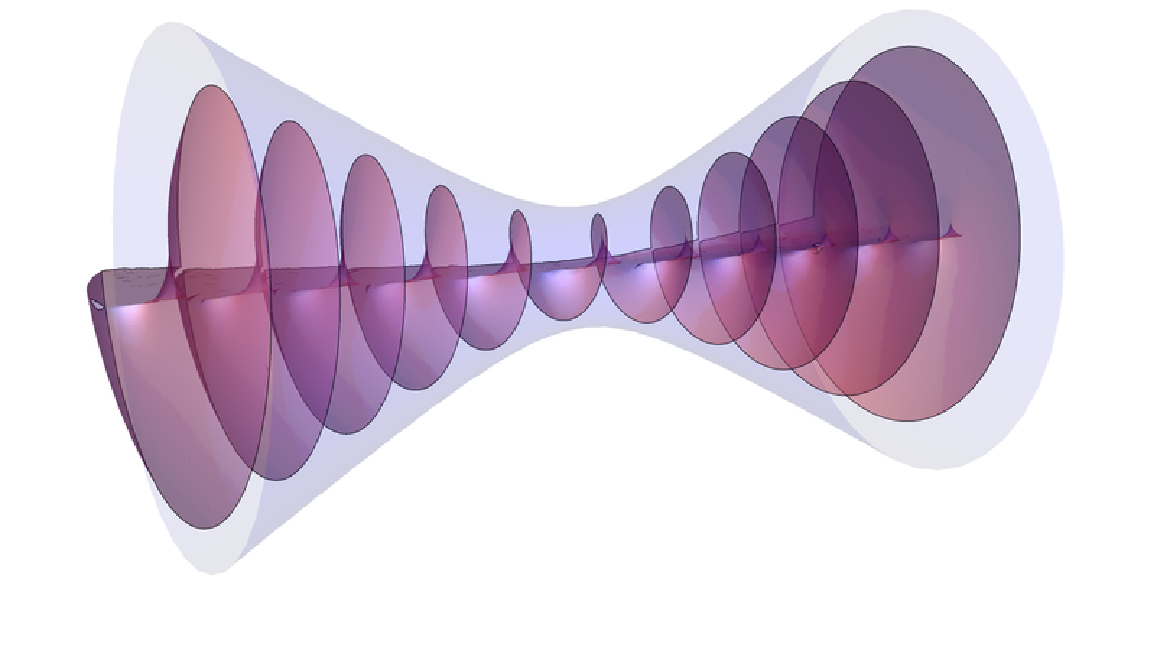
![{time, wavefronts} = AbsoluteTiming[
ContourPlot3D[
ResourceFunction["LaguerreGaussianBeam"][{"Phase", {1, 2, 1, 0}}][
x, y, z], {x, -5, 5}, {y, -5, 5}, {z, -10, 10}, Sequence[
RegionFunction -> Function[{x, y, z, f}, z^2 > 4 (x^2 + y^2 - 1)],
Contours -> Subdivide[-32, 32, 10], ContourStyle -> Directive[
Specularity[20],
Opacity[0.5, Purple]], Mesh -> None, RegionBoundaryStyle -> None]]];
time](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/2ba8ac094958ca15.png)
![volume = ResourceFunction["ExtractGraphicsPrimitives"]@
RevolutionPlot3D[0.6 Sqrt[4 + z^2], {z, -8, 8}, Sequence[
RevolutionAxis -> {1, 0, 0}, Mesh -> None, PlotStyle -> Opacity[0.1, Blue], PlotPoints -> 20]];
Show[Graphics3D[{Rotate[
volume, \[Pi]/2, {0, 1, 0}]}], wavefronts, Sequence[
ViewPoint -> {1.75, 0.31, 0.9}, ViewVertical -> {0, 1, 0}, ImageSize -> 800, Boxed -> False, PlotRange -> {5 {-1, 1}, 5 {-1, 1}, 10 {-1, 1}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/f61/f61e10f4-ebf9-4b68-b29b-537d954e414c/4af7abf8ea094b77.png)