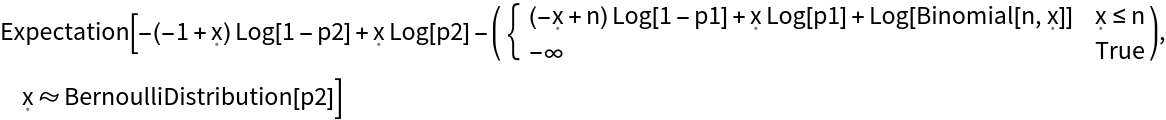Basic Examples (5)
Calculate the KullbackLeiblerDivergence between two normal distributions:
KullbackLeiblerDivergence is not symmetric:
KullbackLeiblerDivergence works with symbolic distributions:
The distributions do not have to be from the same family:
KullbackLeiblerDivergence also works with discrete distributions:
Use a custom-defined ProbabilityDistribution:
Scope (2)
KullbackLeiblerDivergence works for multivariate distributions:
KullbackLeiblerDivergence also works with EmpiricalDistribution:
Options (4)
Method (2)
Symbolic evaluation of the divergence is unfeasible for some distributions:
Use NExpectation instead:
Supply extra options to NExpectation:
NExpectation is designed to work with distributions with numeric parameters:
Assumptions (2)
Without Assumptions, a message will be raised and conditions are generated in the result:
With assumptions specified, a result valid under those conditions is returned:
Applications (2)
If X and Y are two random variables with a joint distribution 𝒟, then the mutual information between them is defined as the Kullback–Leibler divergence from the product distribution of the marginals to 𝒟.
As an example, calculate the mutual information of the components of a BinormalDistribution:
The Kullback–Leibler divergence can be used to fit distributions to data and also provides a measure of the quality of the fit in a way very similar to maximum likelihood estimation. First generate some samples from a discrete distribution:
Calculate the divergence from the EmpiricalDistribution to a symbolic target distribution:
Minimize with respect to μ:
Try a different distribution to compare:
The minimized divergence is larger, indicating this distribution is a worse approximation to the data:
Note that the reverse divergences are not defined because the supports of PoissonDistribution and GeometricDistribution are infinite:
Also note that this does not work for continuous data because the support of EmpiricalDistribution is discrete:
Use a KernelMixtureDistribution instead for continuous data:
Properties and Relations (1)
The divergence from a distribution to itself is zero:
Possible Issues (5)
The dimensions of the distributions have to match:
Matrix distributions are currently not supported:
The divergence is Undefined if the first distribution has a wider support than the second:
KullbackLeiblerDivergence is undefined between discrete and continuous distributions:
For some symbolic distributions the expectation cannot be evaluated:
![ResourceFunction["KullbackLeiblerDivergence"][
ProbabilityDistribution[Sqrt[2]/(
Pi *(1 + \[FormalX]^4)), {\[FormalX], -Infinity, Infinity}],
NormalDistribution[]
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/23e663cb2b36f856.png)
![ResourceFunction["KullbackLeiblerDivergence"][
EmpiricalDistribution[{"a", "b", "b"}],
EmpiricalDistribution[{"a", "b", "c"}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/2139d3a7b3b03a57.png)
![ResourceFunction["KullbackLeiblerDivergence"][
BernoulliDistribution[p],
EmpiricalDistribution[{0, 0, 1}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/3c2f3f024b70ea98.png)
![TimeConstrained[
ResourceFunction["KullbackLeiblerDivergence"][
NormalDistribution[0., 1.], StableDistribution[1, 1.3, 0.5, 0., 2.]], 10]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/60dbcd94497a7d02.png)
![ResourceFunction["KullbackLeiblerDivergence"][
NormalDistribution[0, 1], SetPrecision[StableDistribution[1, 1.3, 0.5, 0., 2.], 20],
Method -> {NExpectation, AccuracyGoal -> 5, PrecisionGoal -> 5, WorkingPrecision -> 20}
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/2b1bff89c628e332.png)
![binormalDist = BinormalDistribution[{\[Mu]1, \[Mu]2}, {\[Sigma]1, \[Sigma]2}, \[Rho]];
ResourceFunction["KullbackLeiblerDivergence"][
binormalDist,
ProductDistribution @@ Map[MarginalDistribution[binormalDist, #] &, {1, 2}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/17a8c28b393ead5c.png)
![ResourceFunction["KullbackLeiblerDivergence"][
EmpiricalDistribution[RandomVariate[NormalDistribution[], 100]],
NormalDistribution[]
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/1cce7700e1680833.png)
![ResourceFunction["KullbackLeiblerDivergence"][
KernelMixtureDistribution[RandomVariate[NormalDistribution[], 100]],
NormalDistribution[],
Method -> NExpectation
]](https://www.wolframcloud.com/obj/resourcesystem/images/24c/24ce1dd0-828d-40e8-bedf-8c3248d44394/0deb24bbb478b5e4.png)